Let I be a countable jump ideal in 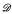= 〈The Turing degrees, ≤〉. The central theorem of this paper is:

a is a uniform upper bound on I iff a computes the join of an I-exact pair whose double jump a(1) computes.

We may replace “the join of an I-exact pair” in the above theorem by “a weak uniform upper bound on I”.

We also answer two minimality questions: the class of uniform upper bounds on I never has a minimal member; if ⋃I = Lα[A] ⋂ ωω for α admissible or a limit of admissibles, the same holds for nice uniform upper bounds.

The central technique used in proving these theorems consists in this: by trial and error construct a generic sequence approximating the desired object; simultaneously settle definitely on finite pieces of that object; make sure that the guessing settles down to the object determined by the limit of these finite pieces.