Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Beklemishev, Lev
and
Gabelaia, David
2013.
Topological completeness of the provability logic GLP.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 12,
p.
1201.
Fernández-Duque, David
2014.
The polytopologies of transfinite provability logic.
Archive for Mathematical Logic,
Vol. 53,
Issue. 3-4,
p.
385.
Beklemishev, Lev D.
Fernández-Duque, David
and
Joosten, Joost J.
2014.
On Provability Logics with Linearly Ordered Modalities.
Studia Logica,
Vol. 102,
Issue. 3,
p.
541.
Beklemishev, Lev
and
Gabelaia, David
2014.
Leo Esakia on Duality in Modal and Intuitionistic Logics.
Vol. 4,
Issue. ,
p.
257.
Fernandez-Duque, D.
and
Joosten, J. J.
2014.
Well-orders in the transfinite Japaridze algebra.
Logic Journal of IGPL,
Vol. 22,
Issue. 6,
p.
933.
Joosten, Joost J.
2015.
Evolving Computability.
Vol. 9136,
Issue. ,
p.
216.
CORDÓN-FRANCO, ANDRÉS
FERNÁNDEZ-DUQUE, DAVID
JOOSTEN, JOOST J.
and
LARA-MARTÍN, FRANCISCO FÉLIX
2017.
PREDICATIVITY THROUGH TRANSFINITE REFLECTION.
The Journal of Symbolic Logic,
Vol. 82,
Issue. 3,
p.
787.
Beklemishev, L. D.
2018.
Reflection calculus and conservativity spectra.
Russian Mathematical Surveys,
Vol. 73,
Issue. 4,
p.
569.
Beklemishev, Lev D.
2018.
Logical Foundations of Computer Science.
Vol. 10703,
Issue. ,
p.
91.
Beklemishev, Lev Dmitrievich
2018.
Исчисление для схем рефлексии и спектры консервативности.
Успехи математических наук,
Vol. 73,
Issue. 4(442),
p.
3.
Fernández-Duque, David
and
Joosten, Joost J.
2018.
The omega-rule interpretation of transfinite provability logic.
Annals of Pure and Applied Logic,
Vol. 169,
Issue. 4,
p.
333.
Fascia, Michael
2019.
Innovation as a Singular Enabler.
SSRN Electronic Journal,
Fernández-Duque, David
Papafilippou, Konstnatinos
and
Joosten, Joost J.
2022.
Logical Foundations of Computer Science.
Vol. 13137,
Issue. ,
p.
52.
Beklemishev, L. D.
2022.
Conservativity Spectra and Joosten–Fernández Model.
Doklady Mathematics,
Vol. 106,
Issue. 1,
p.
213.
Beklemishev, Lev D.
and
Pakhomov, Fedor N.
2022.
Reflection algebras and conservation results for theories of iterated truth.
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 5,
p.
103093.
FernÁndez-Duque, David
Joosten, Joost J
Pakhomov, Fedor
Papafilippou, Konstantinos
and
Weiermann, Andreas
2022.
Arithmetical and Hyperarithmetical Worm Battles.
Journal of Logic and Computation,
Vol. 32,
Issue. 8,
p.
1558.
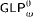 . Later, Icard defined a topological model for
. Later, Icard defined a topological model for 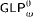 which is very closely related to Ignatiev's.
which is very closely related to Ignatiev's.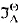 and a topological model
and a topological model 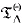 , and show that
, and show that 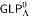 is sound for both of these structures, as well as complete, provided Θ is large enough.
is sound for both of these structures, as well as complete, provided Θ is large enough.

