Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2025-01-03T11:40:50.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Model theory under the axiom of determinateness

Published online by Cambridge University Press:  12 March 2014

Mitchell Spector
Mitchell Spector*
Affiliation:
Department of Mathematics, Eastern Montana College, Billings, Montana 59101-0298
Get access Rights & Permissions [Opens in a new window]

Abstract

We initiate the study of model theory in the absence of the Axiom of Choice, using the Axiom of Determinateness as a powerful substitute. We first show that, in this context, 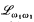is no more powerful than first-order logic. The emphasis then turns to upward Löwenhein-Skolem theorems; ℵ1 is the Hanf number of first-order logic, of 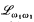, and of a strong fragment of 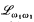, The main technical innovation is the development of iterated ultrapowers using infinite supports; this requires an application of infinite-exponent partition relations. All our theorems can be proven from hypotheses weaker than AD.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 3 , September 1985 , pp. 773 - 780
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[2]Henle, J. M., Researches into the world of κ → (κ)κ, Annals of Mathematical Logic, vol. 17 (1979), pp. 151–169.CrossRefGoogle Scholar
[3]Kechris, A. S., The axiom of determinacy implies dependent choices in L(R), this Journal, vol. 49 (1984), pp. 161–173.Google Scholar
[4]Kechris, A. S., Kleinberg, E. M., Moschovakis, Y. N. and Woodin, W. H., The axiom of determinacy, strong partition properties, and nonsingular measures, Cabal Seminar 77–79 (Kechris, A. S., Martin, D. A. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 839, Springer-Verlag, Berlin, 1981, pp. 75–99.CrossRefGoogle Scholar
[5]Kechris, A. S. and Moschovakis, Y. N. (editors), Cabal Seminar 76–77, Lecture Notes in Mathematics, vol. 689, Springer-Verlag, Berlin, 1978.CrossRefGoogle Scholar
[6]Kleinberg, E. M., Infinitary combinatorics and the axiom of determinateness, Lecture Notes in Mathematics, vol. 612, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[7]Solovay, R. M., A model for set theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, ser. 2, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar