Published online by Cambridge University Press: 12 March 2014
We prove that for a finitely generated infinite nilpotent group G with structure (G, ·, …), the connected component G*0 of a sufficiently saturated extension G* of G exists and equals
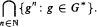
We construct an expansion of ℤ by a predicate (ℤ, +, P) such that the type-connected component 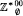 is strictly smaller than ℤ*0. We generalize this to finitely generated virtually solvable groups. As a corollary of our construction we obtain an optimality result for the van der Waerden theorem for finite partitions of groups.
is strictly smaller than ℤ*0. We generalize this to finitely generated virtually solvable groups. As a corollary of our construction we obtain an optimality result for the van der Waerden theorem for finite partitions of groups.