Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-09T22:04:21.311Z Has data issue: false hasContentIssue false
  • English
  • Français

Model Theoretic Algebra1

Published online by Cambridge University Press:  12 March 2014

G. L. Cherlin
G. L. Cherlin*
Affiliation:
Universität Heidelberg, Heidelberg, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Since the late 1940's model theory has found numerous applications to algebra. I would like to indicate some of the points of contact between model theoretic methods and strictly algebraic concerns by means of a few concrete examples and typical applications.

§1. The Lefschetz principle. Algebraic geometry has proved to be a fruitful source of model theoretic ideas. What exactly is algebraic geometry? We consider a field K, and let Kn be the set of n-tuples (a 1 … an ) with coordinates ai in K. Kn is called affine n-space over K. Fix polynomials p 1 …, pk in K[x 1, …, xn ] and define

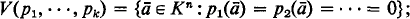
that is V(p 1 …, pk ) is the locus of common zeroes of the pi in Kn . We call V(Pi …, Pk ) the algebraic variety determined by p 1, …, pk . With this terminology we may say:

Algebraic geometry is the study of algebraic varieties defined over an arbitrary field K. This definition lacks both rigor and accuracy, and we will indicate below how it may be improved.

So far we have placed no restrictions on the base field K. Following Weil [4] it is convenient to start with a so-called “universal domain”; in other words take K to be algebraically closed and of infinite transcendence degree over the prime field. Any particular field can of course be embedded in such a universal domain.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 2 , June 1976 , pp. 537 - 545
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Text of a Survey Lecture delivered at the 1974–75 Annual Meeting of the ASL held jointly with the AMS in Washington, D.C., January 1975.

References

REFERENCES

General

[1] Robinson, A., Introduction to model theory and to the metamathematics of algebra, North-Holland, Amsterdam, 1963.Google Scholar
[2] Chang, C. C. and Keisler, J., Model theory, American Elsevier, New York, 1973.Google Scholar
[3] Sacks, G., Saturated model theory, Benjamin, Reading, Massachusetts, 1972.Google Scholar
[4] Weil, A., Foundations of algebraic geometry, AMS Colloquium Publications, vol. 29, Providence, R.I., 1946.Google Scholar
[5] Eklof, P., Lefschetz' principle and local functors, Proceedings of the American Mathematical Society, vol. 37 (1973), pp. 333–339.Google Scholar
[6] Kochen, S., Integer valued rational functions over the p-adic numbers: A p-adic analogue of the theory of real fields, Number theory (Proceedings Symposia in Pure Mathematics, vol. 12), American Mathematical Society, Providence, R.I., 1969, pp. 57–73.Google Scholar
[7] Ax, J. and Kochen, S., Diophantine problems over local fields. I, II, American Journal of Mathematics, vol. 87 (1965), pp. 605–648.CrossRefGoogle Scholar
[8] Kochen, S., Lectures at Kiel 1974, Lecture Notes in Mathematics, Springer-Verlag (to appear).Google Scholar
[9] Ershov, Yu.. Ob elementarnykh teoriyakh lokal'nykh polei, Algebra i Logika, vol. 4 (1965), pp. 5–30.Google Scholar
[10] Ribenboim, P., Théorie des valuations, Université Montréal Press, 1964.Google Scholar
[11] Robinson, A., Nonstandard analysis, North-Holland, Amsterdam, 1968.Google Scholar
[12] Lang, S., Introduction to algebraic geometry, Addison-Wesley, Reading, Massachusetts, 1972.Google Scholar
[13] Eklof, P. and Sabbagh, G., Model completions and modules, Appendix, Annals of Mathematical Logic, vol. 2 (1971), pp. 283–292.CrossRefGoogle Scholar
[14] Barwise, J. and Robinson, A., Completing theories by forcing, Annals of Mathematical Logic, vol. 2 (1970), pp. 119–142.CrossRefGoogle Scholar
[15] Cherlin, G., The model companion of a class of structures, this Journal, vol. 37 (1972), pp. 546–556.Google Scholar
[16] Jacobson, N., Lectures in abstract algebra, vol. III, Van Nostrand, Princeton, N.J., 1964.Google Scholar
[17] Macintyre, A., Omitting quantifier-free types in generic structures, this Journal, vol. 37 (1972), pp. 512–520.Google Scholar
[18] Hirschfeld, J. and Wheeler, W., Forcing, arithmetic, and division rings, Lecture Notes in Mathematics, vol. 454, Springer-Verlag, Berlin and New York, 1975.Google Scholar