Published online by Cambridge University Press: 08 October 2021
It is a classic result in modal logic, often referred to as Jónsson-Tarski duality, that the category of modal algebras is dually equivalent to the category of descriptive frames. The latter are Kripke frames equipped with a Stone topology such that the binary relation is continuous. This duality generalizes the celebrated Stone duality for boolean algebras. Our goal is to generalize descriptive frames so that the topology is an arbitrary compact Hausdorff topology. For this, instead of working with the boolean algebra of clopen subsets of a Stone space, we work with the ring of continuous real-valued functions on a compact Hausdorff space. The main novelty is to define a modal operator on such a ring utilizing a continuous relation on a compact Hausdorff space.
Our starting point is the well-known Gelfand duality between the category 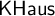 ${\sf KHaus}$
of compact Hausdorff spaces and the category
${\sf KHaus}$
of compact Hausdorff spaces and the category 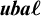 $\boldsymbol {\mathit {uba}\ell }$
of uniformly complete bounded archimedean
$\boldsymbol {\mathit {uba}\ell }$
of uniformly complete bounded archimedean 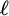 $\ell $
-algebras. We endow a bounded archimedean
$\ell $
-algebras. We endow a bounded archimedean 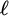 $\ell $
-algebra with a modal operator, which results in the category
$\ell $
-algebra with a modal operator, which results in the category 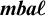 $\boldsymbol {\mathit {mba}\ell }$
of modal bounded archimedean
$\boldsymbol {\mathit {mba}\ell }$
of modal bounded archimedean 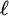 $\ell $
-algebras. Our main result establishes a dual adjunction between
$\ell $
-algebras. Our main result establishes a dual adjunction between 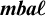 $\boldsymbol {\mathit {mba}\ell }$
and the category
$\boldsymbol {\mathit {mba}\ell }$
and the category 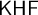 ${\sf KHF}$
of what we call compact Hausdorff frames; that is, Kripke frames equipped with a compact Hausdorff topology such that the binary relation is continuous. This dual adjunction restricts to a dual equivalence between
${\sf KHF}$
of what we call compact Hausdorff frames; that is, Kripke frames equipped with a compact Hausdorff topology such that the binary relation is continuous. This dual adjunction restricts to a dual equivalence between 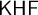 ${\sf KHF}$
and the reflective subcategory
${\sf KHF}$
and the reflective subcategory 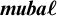 $\boldsymbol {\mathit {muba}\ell }$
of
$\boldsymbol {\mathit {muba}\ell }$
of 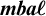 $\boldsymbol {\mathit {mba}\ell }$
consisting of uniformly complete objects of
$\boldsymbol {\mathit {mba}\ell }$
consisting of uniformly complete objects of 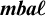 $\boldsymbol {\mathit {mba}\ell }$
. This generalizes both Gelfand duality and Jónsson-Tarski duality.
$\boldsymbol {\mathit {mba}\ell }$
. This generalizes both Gelfand duality and Jónsson-Tarski duality.