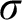Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T12:41:24.433Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MODAL LOGIC OF $\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES

Part of: Set theory General logic

Published online by Cambridge University Press:  03 December 2020

UR YA’AR
UR YA’AR*
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS HEBREW UNIVERSITY OF JERUSALEM EDMOND J. SAFRA CAMPUS GIVAT RAM, JERUSALEM91904, ISRAELE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the modality “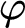 $\varphi $ is true in every 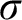$\sigma $ -centered forcing extension,” denoted 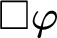$\square \varphi $ , and its dual “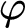 $\varphi $ is true in some 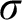$\sigma $ -centered forcing extension,” denoted 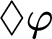$\lozenge \varphi $ (where 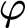$\varphi $ is a statement in set theory), which give rise to the notion of a principle of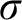 $\sigma $ -centered forcing. 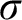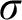We prove that if ZFC is consistent, then the modal logic of $\sigma $ -centered forcing, i.e., the ZFC-provable principles of $\sigma $ -centered forcing, is exactly $\mathsf {S4.2}$ . We also generalize this result to other related classes of forcing.

Keywords

forcingmodal logicmodal logic of forcingsigma-centeredS4.2

MSC classification

Primary: 03E40: Other aspects of forcing and Boolean-valued models
Secondary: 03B45: Modal logic (including the logic of norms)
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 1 , March 2021 , pp. 1 - 24
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barnett, J. H., Weak variants of Martin’s axiom . Fundamenta Mathematicae , vol. 141 (1992), no. 1, pp. 61–73.Google Scholar
U. Ben-Ari-Tishler (now Ya’ar), The modal logic of $\boldsymbol{\sigma}$ - centered forcing and related forcing classes , M.Sc. thesis, Hebrew University of Jerusalem, 2016.Google Scholar
Blackburn, P., de Rijke, M., and Venema, Y., Modal logic , Cambridge Tracts in Theoretical Computer Science, vol. 53, Cambridge University Press, Cambridge, 2001.CrossRefGoogle Scholar
Błaszczyk, A. and Shelah, S., Regular subalgebras of complete Boolean algebras , this Journal, vol. 66 (2001), no. 2, pp. 792–800.Google Scholar
Hamkins, J. D., Leibman, G., and Löwe, B., Structural connections between a forcing class and its modal logic . Israel Journal of Mathematics , vol. 207 (2015), no. 2, pp. 617–651.CrossRefGoogle Scholar
Hamkins, J. D. and Linnebo, Ø., The modal logic of set-theoretic potentialism and the potentialist maximality principles, arXiv preprint, 2017, arXiv:1708.01644 Google Scholar
Hamkins, J. D. and Löwe, B., The modal logic of forcing . Transactions of the American Mathematical Society , vol. 360 (2008), no. 4, pp. 1793–1817.CrossRefGoogle Scholar
Hamkins, J. D. and Löwe, B., Moving up and down in the generic multiverse , Logic and its Applications , Lecture Notes in Computer Science, vol. 7750, Springer, Heidelberg, 2013, pp. 139–147.CrossRefGoogle Scholar
Inamdar, T. C., On the modal logics of some set-theoretic constructions , M.Sc. thesis, Universiteit van Amsterdam, 2013.Google Scholar
Jensen, R. B. and Solovay, R. M., Some applications of almost disjoint sets , Mathematical Logic and Foundations of Set Theory (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
Kunen, K., Set Theory , Studies in Logic, vol. 34, College Publications, London, 2011.Google Scholar
Piribauer, J., The modal logic of generic multiverses , M.Sc. thesis, Universiteit van Amsterdam, 2017.Google Scholar