In this paper we investigate the possibility of extending Friedberg's enumeration of the recursively enumerable (r.e.) sets without duplication [1, p. 312] to meta-recursion theory. It turns out that all of our proposed extensions are impossible save one: the metarecursively enumerable (meta-r.e.) sets can be enumerated without duplication, but only if all the recursive ordinals are used as indices (Theorems 1 and 2). The 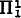sets cannot be so enumerated, even if the index set is all recursive ordinals (Theorems 3 and 4). As a corollary, one proves there is no 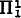predicate P(n, x) with the property that for each 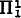set A there is exactly one integer n for which A = {x ∣ P(n, x)}. We also discuss enumerations of nonempty, infinite, and coinfinite 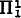and meta-r.e. sets.