Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Halbeisen, Lorenz
and
Löwe, Benedikt
2001.
Techniques for approaching the dual Ramsey property in the projective hierarchy.
Pacific Journal of Mathematics,
Vol. 200,
Issue. 1,
p.
119.
Ikegami, Daisuke
2009.
Projective absoluteness for Sacks forcing.
Archive for Mathematical Logic,
Vol. 48,
Issue. 7,
p.
679.
Ikegami, Daisuke
2010.
Forcing absoluteness and regularity properties.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
879.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
395.
Kanamori, Akihiro
2016.
Mathias and set theory.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 3,
p.
278.
Halbeisen, Lorenz J.
2017.
Combinatorial Set Theory.
p.
517.
Bagaria, Joan
2017.
Logic Colloquium '02.
p.
28.
Müller, Sandra
and
Schlicht, Philipp
2023.
Uniformization and internal absoluteness.
Proceedings of the American Mathematical Society,
Vol. 151,
Issue. 7,
p.
3089.


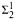 -Sets of reals. This research was motivated by the well-known forcing characterizations for Lebesgue measurability and the Baire property of
-Sets of reals. This research was motivated by the well-known forcing characterizations for Lebesgue measurability and the Baire property of 