Working in ZFC + Martin's Axiom we develop a generalization of the Barwise Compactness Theorem which holds in languages of cardinality less than 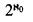. Next, using this compactness theorem, an omitting types theorem for fewer than 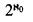types is proved. Finally, in ZFC, we prove that this compactness result implies Martin's Axiom (the Equivalence Theorem). Our compactness theorem applies to a new class of theories—ccΣ-theories—which generalize the countable Σ-theories of Barwise's theorem. The Omitting Types Theorem and the Equivalence Theorem serve as examples illustrating the use of ccΣ-theories.

Assume 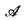= (A, ε) or 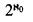= (A, ε R1,…,Rm) where 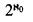is admissible. L(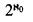) is the first-order language with constants for elements of A and relation symbols for relations in 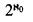. LA is A ⋂ L∞ω where the L of L∞ω is any language in A. A theory T in LA is consistent if there is no derivation in A of a contradiction from T. 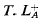is LA with new constants ca for each a and A. The basic terms of 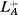consist of the constants of 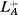and the terms f(ca1,…,cam) built directly from constants using functions f of 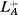. The symbol t is used for basic terms. A theory T in LA is Σ if it is defined by a 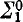formula of L(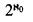). The formula φ⌝ is a logical equivalent of ¬φ defined by: (1) φ⌝ = ¬φ if φ is atomic; (2) (¬φ)⌝ = φ (3) (⋁φ∈Φ φ)⌝ = ⋀φ∈Φ φ⌝; (4) (⋀φ∈Φ φ) ⋁φ∈Φ φ⌝; (5) (∃χφ(x))⌝ ∀χφ⌝(x); ∀χφ(x))⌝ = ∃χφ⌝(x).