Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-31T15:05:59.343Z Has data issue: false hasContentIssue false
  • English
  • Français

A MARRIAGE OF BROUWER’S INTUITIONISM AND HILBERT’S FINITISM I: ARITHMETIC

Part of: Proof theory and constructive mathematics

Published online by Cambridge University Press:  07 January 2021

TAKAKO NEMOTO  and
SATO KENTARO
TAKAKO NEMOTO
Affiliation:
DEPARTMENT OF ARCHITECTURAL DESIGN FACULTY OF ENVIRONMENTAL STUDY HIROSHIMA INSTITUTE OF TECHNOLOGY SAEKI-KU MIYAKE 2-1-1 HIROSHIMA 731-5193, JAPAN E-mail: [email protected]
SATO KENTARO
Affiliation:
INSTITUTE OF COMPUTER SCIENCE UNIVERSITÄT BERN NEUBRÜCKSTRASSE 10 BERN 3012, SWITZERLAND E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

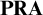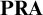We investigate which part of Brouwer’s Intuitionistic Mathematics is finitistically justifiable or guaranteed in Hilbert’s Finitism, in the same way as similar investigations on Classical Mathematics (i.e., which part is equiconsistent with $\textbf {PRA}$ or consistent provably in $\textbf {PRA}$ ) already done quite extensively in proof theory and reverse mathematics. While we already knew a contrast from the classical situation concerning the continuity principle, more contrasts turn out: we show that several principles are finitistically justifiable or guaranteed which are classically not. Among them are: (i) fan theorem for decidable fans but arbitrary bars; (ii) continuity principle and the axiom of choice both for arbitrary formulae; and (iii)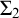 $\Sigma _2$ induction and dependent choice. We also show that Markov’s principle MP does not change this situation; that neither does lesser limited principle of omniscience LLPO (except the choice along functions); but that limited principle of omniscience LPO makes the situation completely classical.

Keywords

Hilbert’s programmeintuitionistic mathematicsRussian recursive mathematicsinterpretabilityconsistency strengthsemi-classical principlefunction-based second order arithmeticLifschitz’s realizabilityKleene’s second modelCoquand–Hofmann forcing

MSC classification

Primary: 03F25: Relative consistency and interpretations
Secondary: 03F35: Second- and higher-order arithmetic and fragments 03F50: Metamathematics of constructive systems 03F55: Intuitionistic mathematics 03F60: Constructive and recursive analysis
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 2 , June 2022 , pp. 437 - 497
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akama, Y., Berardi, S., Hayashi, S., and Kohlenbach, U., An arithmetical hierarchy of the law of excluded middle and related principles, Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science , 2004, IEEE, pp. 192–201.10.1109/LICS.2004.1319613CrossRefGoogle Scholar
Avigad, J., Formalizing forcing arguments in subsystems of second-order arithmetic . Annals of Pure and Applied Logic, vol. 82 (1996), no. 2, pp. 165–191.10.1016/0168-0072(96)00003-6CrossRefGoogle Scholar
Avigad, J., Interpreting classical theories in constructive ones , this Journal, vol. 65 (2000), no. 4, pp. 1785–1812.Google Scholar
Avigad, J. and Feferman, S., Gödel’s functional (“Dialectica”) interpretation, The Handbook of Proof Theory (S. Buss, editor), North-Holland, 1999, pp. 337–405.Google Scholar
Beeson, M. J., Foundations of Constructive Mathematics, Springer, 1985.10.1007/978-3-642-68952-9CrossRefGoogle Scholar
Berger, J., The logical strength of the uniform continuity theorem, Logical Approaches to Computational Barriers, CiE 2006 (A. Beckmann, U. Berger, B. Löwe, and J. V. Tucker, editors), Lecture Notes in Computer Science, Springer, 2006, pp. 35–39.Google Scholar
Berger, J., A separation result for varieties of Brouwer’s fan theorem, Proceedings of the 10th Asian Logic Conference (T. Arai, J. Brendle, C. T. Chong, R. Downey, Q. Feng, H. Kikyo, and H. Ono, editors), World Scientific, 2010, pp. 85–92.Google Scholar
Berger, J. and Bridges, D., A fan-theoretic equivalent of the antithesis of Specker’s theorem . Indagationes Mathematicae, vol. 18 (2007), no. 2, pp. 195–202.10.1016/S0019-3577(07)00012-2CrossRefGoogle Scholar
Bridges, D. and Richman, F., Varieties of Constructive Mathematics, Cambridge University Press, 1987.10.1017/CBO9780511565663CrossRefGoogle Scholar
Burr, W., Fragments of Heyting arithmetic , this Journal, vol. 65 (2000), no. 3, pp. 1223–1240.Google Scholar
Coquand, T. and Hofmann, M., A new method for establishing conservativity of classical systems over their intuitionistic versions . Mathematical Structures in Computer Science, vol. 9 (1999), no. 4, pp. 323–333.10.1017/S0960129599002844CrossRefGoogle Scholar
Diener, H. and Loeb, I., Sequences of real functions on $\left[0,1\right]$ in constructive reverse mathematics. Annals of Pure and Applied Logic, vol. 157 (2009), no. 1, pp. 50–61.10.1016/j.apal.2008.09.018CrossRefGoogle Scholar
Dorais, F. G., Classical consequences of continuous choice principles from intuitionistic analysis . Notre Dame Journal of Fromal Logic, vol. 55 (2014), no. 1, pp. 25–39.Google Scholar
Dummett, M., Elements of Intuitionism, Clarendon Press, 2000.Google Scholar
Feferman, S., Systems of predicative analysis , this Journal, vol. 29 (1964), no. 1, pp. 1–30.Google Scholar
Feferman, S., Recursion theory and set theory: A marriage of convenience, Generalized Recursion Theory II (J. Fenstad, R. Gandy, and G. Sacks, editors), Elsevier, 1978, pp. 55–90.Google Scholar
Fujimoto, K., Truths, inductive definitions, and Kripke-Platek systems over set theory , this Journal, vol. 83 (2018), no. 3, pp. 868–898.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Springer, 1998.Google Scholar
Ishihara, H., Constructive reverse mathematics: Compactness properties, From Sets and Types to Topology and Analysis: Towards Practicable Foundations for Constructive Mathematics (L. Crosilla and P. Schuster, editors), Clarendon Press, 2005, pp. 245–266.Google Scholar
Ishihara, H., Reverse mathematics in Bishop’s constructive mathematics . Philosophia Scientiæ , vol. CS6 (2006), pp. 43–59.Google Scholar
Ishihara, H., Weak König’s lemma implies Brouwer’s fan theorem: A direct proof . Notre Dame Journal of Formal Logic, vol. 47 (2006), no. 2, pp. 249–252.10.1305/ndjfl/1153858649CrossRefGoogle Scholar
Ishihara, H. and Nemoto, T., A note on the independence of premiss rule . Mathematical Logic Quarterly, vol. 62 (2016), no. 1–2, pp. 72–76.10.1002/malq.201500032CrossRefGoogle Scholar
Jäger, G., Rosebrock, T., and Sato, K., Truncation and semi-decidability notions in applicative theories , this Journal, vol. 83 (2018), no. 3, pp. 967–990.Google Scholar
Kohlenbach, U., Effective bounds from ineffective proofs in analysis: An application of functional interpretation and majorization , this Journal, vol. 57 (1992), no. 4, pp. 1239–1273.Google Scholar
Kohlenbach, U., Applied Proof Theory: Proof Interpretations and Their Use in Mathematics, Springer, 2008.Google Scholar
Nemoto, T., Determinacy of Wadge classes and subsystems of second order arithmetic . Mathematical Logic Quarterly, vol. 55 (2009), no. 2, pp. 154–176.10.1002/malq.200710081CrossRefGoogle Scholar
Nemoto, T., Weak weak König’s lemma in constructive reverse mathematics, Proceedings of the 10th Asian Logic Conference (T. Arai, J. Brendle, C. T. Chong, R. Downey, Q. Feng, H. Kikyo, and H. Ono, editors), World Scientific, 2010, pp. 263–270.Google Scholar
Nemoto, T., Finite sets and infinite sets in weak intuitionistic arithmetic . Archive for Mathematical Logic , vol. 59 (2020), no. 5–6, pp. 607–657.Google Scholar
Nemoto, T., A constructive proof of the dense existence of nowhere-differentiable functions in C[0,1] . Computability , vol. 9 (2020), no. 3–4, pp. 315–326.Google Scholar
Nemoto, T. and Sato, K., A Marriage of Brouwer’s Intuitionism and Hilbert’s Finitism II: Set Theory , in preparation.Google Scholar
van Oosten, J., Lifschitz’ realizability , this Journal, vol. 55 (1990), no. 2, pp. 805–821.Google Scholar
Rathjen, M., The realm of ordinal analysis, Sets and Proofs (S. Cooper and J. Truss, editors), Cambridge University Press, 1999, pp. 219–279.Google Scholar
Rathjen, M., Realizability for constructive Zermelo-Fraenkel set theory , Logic Colloquium 2003 (J. Väänänen and V. Stoltenberg-Hansen, editors), Lecture Notes in Logic, vol. 24, Association for Symbolic Logic, 2006, pp. 442–471.10.1201/9781439865835-14CrossRefGoogle Scholar
Rathjen, M., Constructive Zermelo–Fraenkel set theory and the limited principle of omniscience . Annals of Pure and Applied Logic, vol. 165 (2014), no. 2, pp. 563–572.10.1016/j.apal.2013.08.001CrossRefGoogle Scholar
Rüede, C., Transfinite dependent choice and $\omega$ -model reflection, this Journal, vol. 67 (2002), no. 3, pp. 1153–1168.Google Scholar
Rüede, C., The proof-theoretic analysis of ${\varSigma}_1^1$ transfinite dependent choice. Annals of Pure and Applied Logic , vol. 122 (2003), no. 1–3, pp. 195–234.Google Scholar
Sato, K., The strength of extensionality I: Weak weak set theories with infinity . Annals of Pure and Applied Logic, vol. 157 (2009), no. 2–3, pp. 234–268.10.1016/j.apal.2008.09.010CrossRefGoogle Scholar
Sato, K., A new model construction by making a detour via intuitionistic theories II: Interpretability lower bound of Feferman’s explicit mathematics ${T}_0$ . Annals of Pure and Applied Logic , vol. 166 (2015), no. 7–8, pp. 800–835.Google Scholar
Sato, K., A note on predicative ordinal analysis I: Iterated comprehension and transfinite induction , this Journal, vol. 84 (2019), no. 1, pp. 226–265.Google Scholar
Sato, K., Bounded inductive dichotomy: Separation of open and clopen determinacies with finite alternatives in constructive contexts. Archive of Mathematical Logic (2021). https://doi.org/10.1007/s00153-021-00795-2.CrossRefGoogle Scholar
Sato, K., A new model construction by making a detour via intuitionistic theories III: Ultrafinitistic proofs of conservations of ${\varSigma}_1^1$ collection. Annals of Pure and Applied Logic , to appear.Google Scholar
Sato, K., A new model construction by making a detour via intuitionistic theories IV: A closer connection between KP and BI, submitted.Google Scholar
Sato, K. and Zumbrunnen, R., A new model construction by making a detour via intuitionistic theories I: Operational set theory without choice is ${\varPi}_1$ -equivalent to KP. Annals of Pure and Applied Logic , vol. 166 (2015), no. 2, pp. 121–186.Google Scholar
Simpson, S. G., Partial realizations of Hilbert’s Program , this Journal, vol. 53 (1988), no. 2, pp. 349–363.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Cambridge University Press, 2009.10.1017/CBO9780511581007CrossRefGoogle Scholar
Simpson, S. G. and Smith, R. L., Factorization of polynomials and ${\varSigma}_1^0$ induction. Annals of Pure and Applied Logic, vol. 31 (1986), pp. 289–306.10.1016/0168-0072(86)90074-6CrossRefGoogle Scholar
Tait, W. W., Finitism . The Journal of Philosophy, vol. 78 (1981), no. 9, pp. 524–546.10.2307/2026089CrossRefGoogle Scholar
Tait, W. W., Remarks on finitism, Reflections in the Foundations of Mathematic: Essays in Honor of Solomon Feferman (W. Sieg, R. Sommer, and C. Talcott, editors), Lecture Notes in Logic, vol. 15, Association for Symbolic Logic, 2002, pp. 410–419.10.1017/9781316755983.020CrossRefGoogle Scholar
Tapp, C., Eine direkte Einbettung von $\textsf{KP}\omega$ in ${\textsf{ID}}_1$ , Master’s thesis, Diplomarbeit, University of Münster, 1999.Google Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics: An Introduction, vol. I, Elsevier, 1988.Google Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics: An Introduction, vol. II, Elsevier, 1988.Google Scholar
Veldman, W., Two simple sets that are not positively Borel . Annals of Pure and Applied Logic, vol. 135 (2005), no. 1–3, pp. 151–209.10.1016/j.apal.2004.12.004CrossRefGoogle Scholar
Veldman, W., Brouwer’s Fan Theorem as an axiom and as a contrast to Kleene’s Alternative . Archive for Mathematical Logic, vol. 53 (2014), no. 5, pp. 621–693.10.1007/s00153-014-0384-9CrossRefGoogle Scholar
Veldman, W. and Benzem, M., Ramsey’s theorem and the pigeonhole principle in intuitionistic mathematics . Journal of the London Mathematical Society, Second Series, vol. 47 (1993), no. 2, pp. 193–211.10.1112/jlms/s2-47.2.193CrossRefGoogle Scholar
Vesley, R. E., A palatable substitute for Kripke schema, Intuitionism and Proof Theory: Proceedings of the Summer Conference at Buffalo N.Y. 1968 (A. Kino, J. Myhill, and R. Vesley, editors), Elsevier, 1970, pp. 197–207.Google Scholar
Wehmeier, K. F., Fragments of HA based on ${\varSigma}_1$ -induction. Archive for Mathematical Logic, vol. 37 (1997), no. 1, pp. 37–49.10.1007/s001530050081CrossRefGoogle Scholar