Hostname: page-component-5cf477f64f-zrtmk Total loading time: 0 Render date: 2025-04-06T13:09:39.813Z Has data issue: false hasContentIssue false
  • English
  • Français

MARGINALIA ON A THEOREM OF WOODIN

Published online by Cambridge University Press:  21 March 2017

RASMUS BLANCK  and
ALI ENAYAT
RASMUS BLANCK
Affiliation:
DEPARTMENT OF PHILOSOPHY, LINGUISTICS, AND THEORY OF SCIENCE UNIVERSITY OF GOTHENBURG BOX 200, SE 405 30, GOTHENBURG, SWEDENE-mail: [email protected]
ALI ENAYAT
Affiliation:
DEPARTMENT OF PHILOSOPHY, LINGUISTICS, AND THEORY OF SCIENCE UNIVERSITY OF GOTHENBURG BOX 200, SE 405 30, GOTHENBURG, SWEDENE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\left\langle {{W_n}:n \in \omega } \right\rangle$ be a canonical enumeration of recursively enumerable sets, and suppose T is a recursively enumerable extension of PA (Peano Arithmetic) in the same language. Woodin (2011) showed that there exists an index 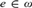$e \in \omega$ (that depends on T) with the property that if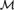${\cal M}$ is a countable model of T and for some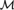${\cal M}$-finite set s, 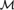${\cal M}$ satisfies 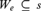${W_e} \subseteq s$, then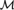${\cal M}$ has an end extension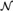${\cal N}$ that satisfies T + We = s.

Here we generalize Woodin’s theorem to all recursively enumerable extensions T of the fragment 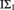${{\rm{I}\rm{\Sigma }}_1}$ of PA, and remove the countability restriction on 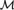${\cal M}$ when T extends PA. We also derive model-theoretic consequences of a classic fixed-point construction of Kripke (1962) and compare them with Woodin’s theorem.

Keywords

03F2503F4003H15Turing machinesPeano arithmeticnonstandard modelsflexible predicatesKolmogorov complexity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 359 - 374
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Avigad, J., Formalizing forcing arguments in subsystems of second-order arithmetic . Annals of Pure and Applied Logic, vol. 82 (1996), pp. 165–191.Google Scholar
Beklemishev, L. and Visser, A., On the limit existence principles in elementary arithmetic and ${\rm{\Sigma }}_n^0$ -consequences of theories . Annals of Pure and Applied Logic, vol. 136 (2005), pp. 56–74.CrossRefGoogle Scholar
Blanck, R., Two consequences of Kripke’s lemma , Idées Fixes (Kaså, Martin, editor), University of Gothenburg Publications, 2014, pp. 45–53.Google Scholar
Boolos, G., The Logic of Provability, Cambridge University Press, Cambridge, 1979.Google Scholar
Cornaros, C., Versions of Friedman’s theorem for fragments of PA, http://www.softlab.ntua.gr/∼nickie/tmp/pls5/cornaros.pdf.Google Scholar
D’Aquino, P., A sharpened version of McAloon’s theorem on initial segments of IΔ0 . Annals of Pure and Applied Logic, vol. 61 (1993), pp. 49–62.Google Scholar
Dimitracopoulos, C. and Paris, J., A note on a theorem of H. Friedman . Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 34 (1988), pp. 13–17.Google Scholar
Dimitracopoulos, C. and Paschalis, V., End extensions of models of weak arithmetic theories . Notre Dame Journal of Formal Logic, to appear.Google Scholar
Enayat, A. and Wong, T., Model theory of ${\rm{WKL}}_0^{^{\rm{*}}}$ . Annals of Pure and Applied Logic, to appear.Google Scholar
Guaspari, D., Partially conservative extensions of arithmetic . Transaction of the American Mathematical Society, vol. 254 (1979), pp. 47–68.Google Scholar
Hájek, P., Interpretability and fragments of arithmetic . Arithmetic, Proof Theory, and Computational Complexity, Oxford University Press, Oxford, 1993, pp. 185–196.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Springer-Verlag, Berlin, 1993.Google Scholar
Japaridze, G. and de Jongh, D., The logic of provability , Handbook of Proof Theory, North-Holland, Amsterdam, 1998, pp. 475–546.Google Scholar
Kaye, R., Models of Peano Arithmetic, Oxford University Press, Oxford, 1991.Google Scholar
Kossak, R. and Schmerl, J., The Structure of Models of Peano Arithmetic, Oxford University Press, Oxford, 2006.Google Scholar
Kripke, S., “Flexible” predicates of formal number theory . Proceedings of the American Mathematical Society, vol. 13 (1962), pp. 647–650.Google Scholar
Lindström, P., Aspects of Incompleteness, Lecture Notes in Logic, vol. 10, ASL Publications, 1997.Google Scholar
McAloon, K., On the complexity of models of arithmetic, this Journal, vol. 47 (1982), pp. 403–415.Google Scholar
Ressayre, J.-P., Nonstandard universes with strong embeddings, and their finite approximations , Logic and Combinatorics, Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 333–358.Google Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability, McGraw-Hill, Cambridge, MA, 1967.Google Scholar
Shen, A., Are random axioms useful? Math. ArXiv, http://arxiv.org/pdf/1109.5526.pdf.Google Scholar
Simpson, S., Subsystems of Second Order Arithmetic, Springer-Verlag, Berlin, 1999.Google Scholar
Smoryński, C., Modal Logic and Self-reference, Springer-Verlag, Berlin, 1985.Google Scholar
Verbrugge, R. and Visser, A., A small reflection principle for bounded arithmetic, this Journal, vol. 59 (1994), pp. 785–812.Google Scholar
Woodin, W. H., A potential subtlety concerning the distinction between determinism and nondeterminism , Infinity, New Research Frontiers (Heller, M. and Woodin, W. H., editors), Cambridge University Press, Cambridge, 2011, pp. 119–129.Google Scholar