No CrossRef data available.
Published online by Cambridge University Press: 30 October 2020
We show that a computable function 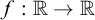 $f:\mathbb R\rightarrow \mathbb R$
has Luzin’s property (N) if and only if it reflects
$f:\mathbb R\rightarrow \mathbb R$
has Luzin’s property (N) if and only if it reflects 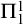 $\Pi ^1_1$
-randomness, if and only if it reflects
$\Pi ^1_1$
-randomness, if and only if it reflects 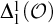 $\Delta ^1_1({\mathcal {O}})$
-randomness, and if and only if it reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness, and if and only if it reflects  ${\mathcal {O}}$
-Kurtz randomness, but reflecting Martin–Löf randomness or weak-2-randomness does not suffice. Here a function f is said to reflect a randomness notion R if whenever
${\mathcal {O}}$
-Kurtz randomness, but reflecting Martin–Löf randomness or weak-2-randomness does not suffice. Here a function f is said to reflect a randomness notion R if whenever 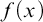 $f(x)$
is R-random, then x is R-random as well. If additionally f is known to have bounded variation, then we show f has Luzin’s (N) if and only if it reflects weak-2-randomness, and if and only if it reflects
$f(x)$
is R-random, then x is R-random as well. If additionally f is known to have bounded variation, then we show f has Luzin’s (N) if and only if it reflects weak-2-randomness, and if and only if it reflects 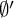 $\emptyset '$
-Kurtz randomness. This links classical real analysis with algorithmic randomness.
$\emptyset '$
-Kurtz randomness. This links classical real analysis with algorithmic randomness.