Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Steiner, Rebecca M.
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
696.


 . For such subalgebras
. For such subalgebras 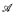 , we show that it is possible for the spectrum of the unary relation
, we show that it is possible for the spectrum of the unary relation 