No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
We study low level nondefinability in the Turing degrees. We prove a variety of results, including, for example, that being array nonrecursive is not definable by a Σ1 or Π1 formula in the language (≤, REA) where REA stands for the “r.e. in and above” predicate. In contrast, this property is definable by a Π2 formula in this language. We also show that the Σ1-theory of (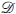 , ≤, REA) is decidable.
, ≤, REA) is decidable.