Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T23:29:22.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit ultraproducts

Published online by Cambridge University Press:  12 March 2014

H. Jerome Keisler
H. Jerome Keisler*
Affiliation:
University of Wisconsin
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a sequel to our earlier paper, “Limit Ultrapowers”, [6]. In that paper we introduced the limit ultrapower construction and proved that 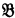is isomorphic to a limit ultrapower of 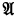if and only if every PCΔ class which contains 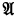also contains 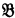. In Section 1 of this paper we introduce the more general limit ultraproduct construction, and in Section 2 we prove that, for any class K of relational systems, a relational system 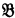is isomorphic to a limit ultraproduct of members of K if and only if every PCΔ class which includes K also contains 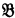. As a consequence, the property of K being an intersection of PCΔ classes is characterized purely set-theoretically by the property of K being closed under isomorphisms and limit ultraproducts.

In Section 3 we apply limit ultraproducts to obtain model-theoretic conditions equivalent to the set-theoretic condition that every α-complete ultrafilter is γ+-complete. The first result, Theorem 3.7, was announced in the abstract [8], and it is also closely related to a result which was stated without proof in [10], namely Theorem 2 of that paper.

In Sections 4 and 5 we apply our results in order to improve a theorem of Craig in [2]. Craig considered the logic L(Q), where Q is a set of cardinals, obtained from ordinary first order logic by adding for each α ϵ Q the quantifier “there exist at least α”.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 30 , Issue 2 , June 1965 , pp. 212 - 234
Copyright
Copyright © Association for Symbolic Logic 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Continuous Model Theory, Princeton, Annals of Mathematics Studies, to appear.CrossRefGoogle Scholar
[2]Craig, W., Relative characterizability and generalized existential quantifiers, Notices American Mathematical Society, vol. 9 (1962), p. 153, Abstract 62T-96.Google Scholar
[3]Craig, W. and Hanf, W., On relative characterizability in a language, Notices American Mathematical Society, vol. 9 (1962), pp. 152–153, Abstract 62T-95.Google Scholar
[4]Frayne, T., Morel, A. C. and Scott, D., Reduced direct products, Fundamenta Mathematicae, vol. 51 (1962), pp. 195–228.CrossRefGoogle Scholar
[5]Fuhrken, G., On generalized quantifiers (abstract), Notices American Mathematical Society, vol. 9 (1962), p. 132.Google Scholar
[6]Keisler, H. J., Limit ultrapowers, Transactions American Mathematical Society, vol. 107 (1963), pp. 382–408.CrossRefGoogle Scholar
[7]Keisler, H. J., Limit reduced products, Notices American Mathematical Society, vol. 6 (1959), p. 520 (Abstract 559-137).Google Scholar
[8]Keisler, H. J., The equivalence of certain problems in set theory with problems in the theory of models, Notices American Mathematical Society, vol. 9 (1962), pp. 339–340, Abstract 62T-257.Google Scholar
[9]Keisler, H. J., Intersections of PCΔ classes, Notices American Mathematical Society, vol. 10 (1963), p. 137, Abstract 63T-48. Errata, Notices American Mathematical Society, vol. 10 (1963), p. 377.Google Scholar
[10]Keisler, H. J., Some applications of the theory of models to set theory. An article in Logic, Methodology, and the Philosophy of Science, pp. 80–86, Stanford, 1962.Google Scholar
[11]Keisler, H. J., On cardinalities of ultrapowers, Bulletin American Mathematical Society, vol. 70 (1964), pp. 644–647.CrossRefGoogle Scholar
[12]Keisler, H. J. and Tarski, A., From accessible to inaccessible cardinals, Fundamentia Mathematicae, vol. 53 (1964), pp. 225–308.CrossRefGoogle Scholar
[13]Kochen, S., Ultraproducts in the theory of models, Annals of Mathematics, vol. 74 (1961), pp. 221–261.CrossRefGoogle Scholar
[14]Morley, M. and Vaught, R., Homogeneous universal models, Mathematica Scandinavica, vol. 11 (1962), pp. 37–57.CrossRefGoogle Scholar
[15]Mostowski, A., On a generalization of quantifiers, Fundamenta Mathematicae, vol. 44 (1957), pp. 12–36.CrossRefGoogle Scholar
[16]Rabin, M. O., Arithmetical extensions with prescribed cardinality, Indagationes Mathematicae, vol. 21 (1959), pp. 439–446.CrossRefGoogle Scholar
[17]Tarski, A., Quelques theorems sur les alephs, Fundamenta Mathematicae, vol. 7 (1925), pp. 1–14.CrossRefGoogle Scholar
[18]Tarski, A., Contributions to the theory of models, I and II, Indagationes Mathematicae, vol. 16 (1954), pp. 572–588.CrossRefGoogle Scholar
[19]Tarski, A., Some model-theoretic results concerning weak second-order logic, Notices American Mathematical Society, vol. 6 (1958), p. 673, Abstract 550-6.Google Scholar