For integers l ≥ 1, d ≥ 0 we study (undirected) graphs with vertices 1, …, n such that the vertices can be partitioned into l parts such that every vertex has at most d neighbours in its own part. The set of all such graphs is denoted Pn (l, d). We prove a labelled first-order limit law, i.e., for every first-order sentence φ, the proportion of graphs in Pn (l, d) that satisfy φ converges as n → ∞. By combining this result with a result of Hundack, Prömel and Steger [12] we also prove that if 1 ≤ s1 ≤ … ≤ sl are integers, then Forb(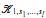) has a labelled first-order limit law, where Forb(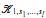) denotes the set of all graphs with vertices 1, …, n, for some n, in which there is no subgraph isomorphic to the complete (l + 1 )-partite graph with parts of sizes 1, s1, …, sl. In the course of doing this we also prove that there exists a first-order formula ξ, depending only on l and d, such that the proportion of ∈ Pn (l, d) with the following property approaches 1 as n → ∞: there is a unique partition of {1, …, n} into l parts such that every vertex has at most d neighbours in its own part, and this partition, viewed as an equivalence relation, is defined by ξ.