Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-01T20:52:05.622Z Has data issue: false hasContentIssue false
  • English
  • Français

LEARNING EQUIVALENCE RELATIONS ON POLISH SPACES

Part of: Computability and recursion theory Theory of computing Set theory

Published online by Cambridge University Press:  03 February 2025

DINO ROSSEGGER Open the ORCID record for DINO ROSSEGGER [Opens in a new window] ,
THEODORE SLAMAN Open the ORCID record for THEODORE SLAMAN [Opens in a new window]  and
TOMASZ STEIFER Open the ORCID record for TOMASZ STEIFER [Opens in a new window]
DINO ROSSEGGER*
Affiliation:
INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY TECHNISCHE UNIVERSITÄT WIEN VIENNA, AUSTRIA
THEODORE SLAMAN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA BERKELEY, CA, USA E-mail: [email protected]
TOMASZ STEIFER
Affiliation:
UNIVERSIDAD CATÓLICA DE CHILE & INSTITUTE OF FUNDAMENTAL TECHNOLOGICAL RESEARCH POLISH ACADEMY OF SCIENCES WARSAW, POLAND E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate natural variations of behaviourally correct learning and explanatory learning—two learning paradigms studied in algorithmic learning theory—that allow us to “learn” equivalence relations on Polish spaces. We give a characterization of the learnable equivalence relations in terms of their Borel complexity and show that the behaviourally correct and explanatory learnable equivalence relations coincide both in uniform and non-uniform versions of learnability and provide a characterization of the learnable equivalence relations in terms of their Borel complexity. We also show that the set of uniformly learnable equivalence relations is 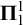$\boldsymbol {\Pi }^1_1$-complete in the codes and study the learnability of several equivalence relations arising naturally in logic as a case study.

Keywords

computational learning theoryBorel equivalence relationequivalence relation

MSC classification

Primary: 03E15: Descriptive set theory 68Q32: Computational learning theory
Secondary: 03D80: Applications of computability and recursion theory
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy. Stud. Logic Found. Math., vol. 144. North-Holland Publishing Co., Amsterdam, 2000.Google Scholar
Bazhenov, N., Cipriani, V., and Mauro, L. S., Learning algebraic structures with the help of Borel equivalence relations. Theoretical Computer Science , vol. 951 (2023), p. 113762.Google Scholar
Bazhenov, N., Fokina, E., and Mauro, L. S., Learning families of algebraic structures from informant. Information and Computation , vol. 275 (2020), p. 104590.Google Scholar
Chong, C. T. and Yu, L., Recursion theory, Logic and its Applications , vol. 8. de Gruyter, Berlin, 2015.Google Scholar
Dougherty, R., Jackson, S., and Kechris, A. S., The structure of hyperfinite Borel equivalence relations. Transactions of the American Mathematical Society , vol. 341 (1994), no. 1, pp. 193–225.Google Scholar
Feldman, J. A., Some decidability results on grammatical inference and complexity. Information and Control , vol. 20 (1972), no. 3, pp. 244–262.Google Scholar
Fokina, E., Kötzing, T., and Mauro, L. S., Limit learning equivalence structures. In Proceedings of the 30th International Conference on Algorithmic Learning Theory, edited by Aurélien Garivier and Satyen Kale, 98:383–403. Proceedings of Machine Learning Research. PMLR. http://proceedings.mlr.press/v98/fokina19a.html.Google Scholar
Gold, E. M., Language identification in the limit. Information and Control , vol. 10 (1967), no. 5, pp. 447–474.Google Scholar
Harrison, J., Recursive pseudo-well-orderings. Transactions of the American Mathematical Society , vol. 131 (1968), no. 2, pp. 526–543.Google Scholar
Hjorth, G. and Kechris, A. S., Borel equivalence relations and classifications of countable models. Annals of Pure and Applied Logic , vol. 82 (1996), no. 3, pp. 221–272.Google Scholar
Kechris, A., Classical Descriptive Set Theory , vol. 156. Graduate Texts in Mathematics. Springer Science & Business Media, New York, 1995.Google Scholar
Kechris, A., The Theory of Countable Borel Equivalence Relations. Cambridge Tracts in Mathematics. Cambridge: Cambridge University Press. https://doi.org/10.1017/9781009562256.Google Scholar
Lecomte, D., On the complexity of Borel equivalence relations with some countability property. Transactions of the American Mathematical Society , vol. 373 (2020), no. 3, pp. 1845–1883.Google Scholar
Louveau, A., A separation theorem for $\varSigma \widehat{1}\_1$ sets. Transactions of the American Mathematical Society , vol. 260 (1980), no. 2, pp. 363–378.Google Scholar
Louveau, A., On the Reducibility Order between Borel Equivalence Relations , In Studies in Logic and the Foundations of Mathematics (Vol. 134, pp. 151–155). North-Holland Publishing Company, Amsterdam, 1994.Google Scholar
Miller, A. W., On the Borel classification of the isomorphism class of a countable model. Notre Dame Journal of Formal Logic , vol. 24 (1983), no. 1, pp. 22–34.Google Scholar
Montalbán, A., Computable Structure Theory: Beyond the Arithmetic. Draft, preprint, 2023. https://math.berkeley.edu/~antonio/CSTpart2_draft.pdf Google Scholar
Rosendal, C., Cofinal families of Borel equivalence relations and quasiorders. The Journal of Symbolic Logic , vol. 70 (2005), no. 4, pp. 1325–1340.Google Scholar
Wadge, W. W., Reducibility and Determinateness on the Baire Space , University of California, Berkeley, 1983.Google Scholar