Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fischer, Arthur
Goldstern, Martin
Kellner, Jakob
and
Shelah, Saharon
2017.
Creature forcing and five cardinal characteristics in Cichoń’s diagram.
Archive for Mathematical Logic,
Vol. 56,
Issue. 7-8,
p.
1045.
Fischer, Vera
and
Alejandro Mejia, Diego
2017.
Splitting, Bounding, and Almost
Disjointness Can Be Quite Different.
Canadian Journal of Mathematics,
Vol. 69,
Issue. 3,
p.
502.
GAVALOVÁ, VIERA
and
MEJÍA, DIEGO A.
2023.
LEBESGUE MEASURE ZERO MODULO IDEALS ON THE NATURAL NUMBERS.
The Journal of Symbolic Logic,
p.
1.


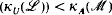 is consistent with ZFC.
is consistent with ZFC.