Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T20:48:10.014Z Has data issue: false hasContentIssue false
  • English
  • Français

A large power set axiom

Published online by Cambridge University Press:  12 March 2014

Paul E. Cohen
Paul E. Cohen*
Affiliation:
Institute for Advanced Study, Princeton, New Jersey 08540
Get access Rights & Permissions [Opens in a new window]

Extract

Takeuti [6] has suggested the need for higher axioms for set theory which are analogous to higher axioms of infinity, but which claim that power sets are in some sense large. In this paper we investigate a reflection axiom of this sort (Axiom T).

In §1, we introduce Axiom T and explore some related axioms. A technical lemma involving an elementary embedding is developed in §2 which allows us, in §3, to prove the relative consistency of Axiom T.

The reader is assumed to be familiar with ramified forcing languages and the usual techniques of forcing. A suitable treatment of these subjects is given by Takeuti and Zaring [7].

ZFC, GBC, ZF and GB are the set theories of Zermelo-Fraenkel and of Gödel-Bernays, with and without the axiom of choice (AC). CH is the continuum hypothesis.

For α an ordinal, define

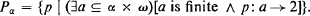
For p1, p2 ∈ pα let p1 ≤ p2 mean that p1 ⊇ p2 (thus p1 is the stronger forcing condition). It is well known that Pα satisfies the countable chain condition [5].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 1 , March 1975 , pp. 48 - 54
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Cohen, P. E., Models of set theory with more real numbers than ordinals, this Journal, vol. 39 (1974), pp. 579–583.Google Scholar
[2]Cohen, P. E., Some applications of forcing in set theory, Doctoral Dissertation, University of Illinois, Champaign-Urbana, 1972.Google Scholar
[3]Cohen, P. J., Set theory and the continuum hypothesis, Benjamin, New York, 1966.Google Scholar
[4]Hanf, W. and Scott, D., Classifying inaccessible cardinals, Notices of the American Mathematical Society, vol. 8 (1961), p. 445.Google Scholar
[5]Shoenfield, J., Unramified forcing, Proceedings of Symposia in Pure Mathematics, vol. 13, part I, American Mathematical Society, Providence, R.I., 1971, pp. 357–381.Google Scholar
[6]Takeuti, G., Hypotheses on power set, Proceedings of Symposia in Pure Mathematics, vol. 13, part I, American Mathematical Society, Providence, R.I., 1971, pp. 439–446.Google Scholar
[7]Takeuti, G. and Zaring, W., Axiomatic set theory, Springer-Verlag, New York, 1973.CrossRefGoogle Scholar