Hostname: page-component-5cf477f64f-zrtmk Total loading time: 0 Render date: 2025-03-28T23:13:06.969Z Has data issue: false hasContentIssue false
  • English
  • Français

ITERATION THEOREMS FOR SUBVERSIONS OF FORCING CLASSES

Part of: Set theory

Published online by Cambridge University Press:  17 March 2025

GUNTER FUCHS Open the ORCID record for GUNTER FUCHS [Opens in a new window]  and
COREY BACAL SWITZER Open the ORCID record for COREY BACAL SWITZER [Opens in a new window]
GUNTER FUCHS*
Affiliation:
DEPARTMENT OF MATHEMATICS THE GRADUATE CENTER OF THE CITY UNIVERSITY OF NEW YORK 365 FIFTH AVENUE, NEW YORK, NY 10016, USA AND DEPARTMENT OF MATHEMATICS, CUNY COLLEGE OF STATEN ISLAND 2800 VICTORY BOULEVARD, STATEN ISLAND NY 10314, USA URL: http://www.math.csi.cuny/edu/~fuchs
COREY BACAL SWITZER
Affiliation:
INSTITUTE OF MATHEMATICS, UNIVERSITY OF VIENNA KOLINGASSE 14-16, 1090 VIENNA AUSTRIA E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove various iteration theorems for forcing classes related to subproper and subcomplete forcing, introduced by Jensen. In the first part, we use revised countable support iterations, and show that 1) the class of subproper, 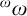${}^\omega \omega $-bounding forcing notions, 2) the class of subproper, T-preserving forcing notions (where T is a fixed Souslin tree) and 3) the class of subproper, 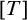$[T]$-preserving forcing notions (where T is an $\omega _1$-tree) are iterable with revised countable support. In the second part, we adopt Miyamoto’s theory of nice iterations, rather than revised countable support. We show that this approach allows us to drop a technical condition in the definitions of subcompleteness and subproperness, still resulting in forcing classes that are iterable in this way, preserve 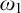$\omega _1$, and, in the case of subcompleteness, don’t add reals. Further, we show that the analogs of the iteration theorems proved in the first part for RCS iterations hold for nice iterations as well.

Keywords

iterated forcingrevised countable supportsubcomplete forcing

MSC classification

Primary: 03E50: Continuum hypothesis and Martin's axiom 03E55: Large cardinals 03E57: Generic absoluteness and forcing axioms 03E35: Consistency and independence results 03E17: Cardinal characteristics of the continuum
Secondary: 03E05: Other combinatorial set theory 03E40: Other aspects of forcing and Boolean-valued models
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 51
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham, U., Proper forcing , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Berlin, Heidelberg, Dordrecht, New York, 2010.Google Scholar
Fuchs, G., Closure properties of parametric subcompleteness . Archive for Mathematical Logic, vol. 57 (2018), nos. 7–8, pp. 829–852.CrossRefGoogle Scholar
Fuchs, G., Hierarchies of forcing axioms, the continuum hypothesis and square principles . Journal of Symbolic Logic, vol. 83 (2018), no. 1, pp. 256–282.CrossRefGoogle Scholar
Fuchs, G., Diagonal reflections on squares . Archive for Mathematical Logic, vol. 58 (2019), no. 1, pp. 1–26.CrossRefGoogle Scholar
Fuchs, G., Canonical fragments of the strong reflection principle . Journal of Mathematical Logic, vol. 21 (2021), no. 03, 2150023.CrossRefGoogle Scholar
Fuchs, G., Errata: On the role of the continuum hypothesis in forcing principles for subcomplete forcing . Archive for Mathematical Logic, vol. 63 (2024), pp. 509–521.CrossRefGoogle Scholar
Fuchs, G. and Minden, K., Subcomplete forcing, trees and generic absoluteness . Journal of Symbolic Logic, vol. 83 (2018), no. 3, pp. 1282–1305.CrossRefGoogle Scholar
Goldstern, M. and Shelah, S., The bounded proper forcing axiom . Journal of Symbolic Logic, vol. 60 (1995), no. 1, pp. 58–73.CrossRefGoogle Scholar
Jensen, R. B., Dee-subproper forcing. Handwritten notes, 2008.Google Scholar
Jensen, R. B., The extended Namba problem. Handwritten notes, 2009.Google Scholar
Jensen, R. B., Forcing axioms compatible with CH. Handwritten notes, 2009.Google Scholar
Jensen, R. B., Subproper and subcomplete forcing. Handwritten notes, 2009.Google Scholar
Jensen, R. B., Subcomplete forcing and -forcing, E-Recursion, Forcing and ${\boldsymbol{C}}^{\ast}$ - Algebras (Chong, C., Feng, Q., Slaman, T. A., Woodin, W. H., and Yang, Y., editors), Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, 27, World Scientific, Singapore, 2014, pp. 83–182.Google Scholar
Jensen, R. B., Iteration theorems for subcomplete and related forcings. Handwritten notes, 2014–15.Google Scholar
Miyamoto, T., Iterated forcing with ${\omega}^{\omega }$ -bounding and semiproper preorders . RIMS Kokyuroku 1202 (Axiomatic Set Theory), Kyoto University Institute for Mathematics, 2001, pp. 83–99. http://hdl.handle.net/2433/40961 Google Scholar
Miyamoto, T., On iterating semiproper preorders . Journal of Symbolic Logic, vol. 67 (2002), no. 4, pp. 1431–1468.CrossRefGoogle Scholar
Miyamoto, T., A class of preorders iterated under a type of RCS . RIMS Kokyuroku, vol. 1754 (2011), pp. 81–90.Google Scholar
Viale, M., Audrito, G., and Steila, S., A Boolean algebraic approach to semiproper iterations, preprint, 2014, arXiv:1402.1714 [math.LO].Google Scholar