Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-09T05:07:58.433Z Has data issue: false hasContentIssue false
  • English
  • Français

The isomorphism property in nonstandard analysis and its use in the theory of Banach spaces

Published online by Cambridge University Press:  12 March 2014

C. Ward Henson
C. Ward Henson*
Affiliation:
Duke University, Durham, North Carolina 27706
Get access Rights & Permissions [Opens in a new window]

Extract

The basic setting of nonstandard analysis consists of a set-theoretical structure 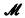together with a map * from 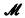into another structure * 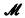of the same sort. The function * is taken to be an elementary embedding (in an appropriate sense) and is generally assumed to make * 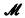into an enlargement of 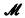[13]. The structures 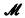and *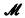 may be type-hierarchies as in [11] and [13] or they may be cumulative structures with ω levels as in [14]. The assumption that * 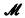is an enlargement of 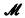has been found to be the weakest hypothesis which allows for the familiar applications of nonstandard analysis in calculus, elementary topology, etc. Indeed, practice has shown that a smooth and useful theory can be achieved only by assuming also that * 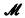has some stronger properties such as the saturation properties first introduced in nonstandard analysis by Luxemburg [11].

This paper concerns an entirely new family of properties, stronger than the saturation properties. For each cardinal number κ, *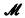 satisfies the κ-isomorphism property (as an enlargement of 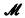) if the following condition holds:

For each first order language L with fewer than κ nonlogical symbols, if 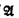and 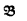are elementarily equivalent structures for L whose domains, relations and functions are all internal (relative to * 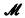and 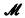), then 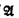and 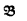are isomorphic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 4 , December 1974 , pp. 717 - 731
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Amir, D. and Lindenstrauss, J., The structure of weakly compact sets in Banach spaces, Annals of Mathematics, vol. 88 (1968), pp. 35–46.Google Scholar
[2] Cozart, D. and Moore, L. C. Jr., The nonstandard hull of a normed Riesz space, Duke Mathematics Journal (to appear).Google Scholar
[3] Henson, C. Ward and Moore, L. C. Jr., The nonstandard theory of topological vector spaces, Transactions of the American Mathematical Society, vol. 172 (1972), pp. 405–435.CrossRefGoogle Scholar
[4] Henson, C. Ward and Moore, L. C. Jr., Subspaces of the nonstandard hull of a normed space, Transactions of the American Mathematical Society (to appear).Google Scholar
[5] John, K. and Zizler, V., Projections in dual weakly compactly generated Banach spaces, Studia Mathematica, vol. 49 (1973), pp. 41–50.CrossRefGoogle Scholar
[6] Lindenstrauss, J., On reflexive spaces having the metric approximation property, Israel Journal of Mathematics, vol. 3 (1965), pp. 199–204.Google Scholar
[7] Lindenstrauss, J., On nonseparable reflexive Banach spaces, Bulletin of the American Mathematical Society, vol. 72 (1966), pp. 967–970.CrossRefGoogle Scholar
[8] Lindenstrauss, J., On a theorem of Mackey and Murray, Anais da Academia Brastieira de Ciencias, vol. 39 (1967), pp. 1–6.Google Scholar
[9] Lindenstrauss, J., Weakly compact sets—Their topological properties and the Banach spaces they generate (Symposium on Infinite dimensional topology, Anderson, R. D., Editor), Annals of Mathematics Studies, No. 69, Princeton University Press, Princeton, N.J., 1972, pp. 235–273.Google Scholar
[10] Lindenstrauss, J. and Rosenthal, H. P., The spaces, Israel Journal of Mathematics, vol. 7 (1969), pp. 325–349.Google Scholar
[11] Luxemburg, W. A. J., A general theory of monads, Applications of model theory to algebra, analysis and probability (Luxemburg, W. A. J., Editor), Holt, Rinehart and Winston, New York, 1969, pp. 18–86.Google Scholar
[12] Luxemburg, W. A. J., On some concurrent binary relations occurring in analysis, Contributions to nonstandard analysis (Luxemburg, W. A. J. and Robinson, A., Editors), North-Holland, Amsterdam, 1972, pp. 85–100.Google Scholar
[13] Robinson, A., Non-standard analysis, North-Holland, Amsterdam, 1966.Google Scholar
[14] Robinson, A. and Zakon, E., A set-theoretical characterization of enlargements, Applications of model theory to algebra, analysis and probability (Luxemburg, W. A. J., Editor), Holt, Rinehart and Winston, New York, 1969, pp. 109–122.Google Scholar
[15] Skolem, T., Untersuchungen über die Axioms des Klassenkalküls und über die “Productations und Summationsprobleme”, welche gewissen Klassen von Aussagen betreffen, Skrifter utgit av Videnskapsselskapet i Kristiania. I, Klasse no. 3, Oslo, 1919.Google Scholar
[16] Shoenfield, J. R., Mathematical logic, Addison-Wesley, Reading, Mass., 1967.Google Scholar
[17] Tarski, A., Arithmetical classes and types of Boolean algebras (Preliminary report), Bulletin of the American Mathematical Society, vol. 55 (1949), p. 64.Google Scholar