Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T04:51:48.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse topological systems and compactness in abstract model theory

Published online by Cambridge University Press:  12 March 2014

Daniele Mundici
Daniele Mundici*
Affiliation:
Loc. Romola N. 76, 50060 Donnini, Florence, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an abstract logic 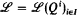, generated by a set of quantifiers Qi, one can construct for each type τ a topological space Sτ, exactly as one constructs the Stone space for τ in first-order logic. Letting T be an arbitrary directed set of types, the set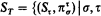 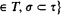is an inverse topological system whose bonding mappings 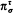are naturally determined by the reduct operation on structures. We relate the compactness of to the topological properties of ST. For example, if I is countable then 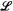is compact iff for every τ each clopen subset of Sτ is of finite type and Sτ, is homeomorphic to limST, where T is the set of finite subtypes of τ. We finally apply our results to concrete logics.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 3 , September 1986 , pp. 785 - 794
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, K. J., Axioms for abstract model theory, Annals of Mathematical Logic, vol. 7 (1974), pp. 221–265.CrossRefGoogle Scholar
[2]Barwise, K. J. and Feferman, S. (editors), Model-theoretic logics, Springer-Verlag, New York, 1985.Google Scholar
[3]Barwise, K. J., Kaufmann, M. and Makkai, M., Stationary logic, Annals of Mathematical Logic, vol. 13 (1978), pp. 171–224.CrossRefGoogle Scholar
[4]Ebbinghaus, H. D., Extended logics: the general framework, Chapter II in [2].Google Scholar
[5]Engelking, R., General topology, PWN, Warsaw, 1977.Google Scholar
[6]Keisler, H. J., Logic with the quantifier “there exist uncountably many”, Annals of Mathematical Logic, vol. 1 (1970), pp. 1–93.CrossRefGoogle Scholar
[7]Lindström, P., On extensions of elementary logic, Theoria, vol. 35 (1969), pp. 1–11.CrossRefGoogle Scholar
[8]Magidor, M. and Malitz, J., Compact extensions of L(Q), Annals of Mathematical Logic, vol. 12 (1977), pp. 217–261.CrossRefGoogle Scholar
[9]Makowsky, J. A. and Mundici, D., Abstract equivalence relations, Chapter XIX in [2].Google Scholar
[10]Mundici, D., Applications of many-sorted Robinson consistency theorem, Zeitschrift für Mathematische Logik and Grundlagen der Mathematik, vol. 27 (1981), pp. 181–188.CrossRefGoogle Scholar
[11]Mundici, D., Duality between logics and equivalence relations, Transactions of the American Mathematical Society, vol. 270 (1982), pp. 111–129.CrossRefGoogle Scholar
[12]Mundici, D., Other quantifiers: an overview, Chapter VI in [2].Google Scholar
[13]Shelah, S., Generalized quantifiers and compact logics, Transactions of the American Mathematical Society, vol. 204 (1975), pp. 342–364.CrossRefGoogle Scholar
[14]Mundici, D., Abstract model-theory and nets of C*-algebras: noncommutative interpolation and preservation properties, Models and sets (Proceedings of Logic Colloquium '83, Part 1), Lecture Notes in Mathematics, vol. 1103, Springer-Verlag, Berlin, 1984, pp. 351–377.Google Scholar
[15]Mundici, D., Mapping Abelian l-groups with strong unit one-one into MV algebras, Journal of Algebra, vol. 98 (1986), pp. 76–81.CrossRefGoogle Scholar
[16]Mundici, D., Interpolation of AF C*-algebras in Lukasiewicz sentential calculus, Journal of Functional Analysis, vol. 65 (1986), pp. 15–63.CrossRefGoogle Scholar