Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-31T19:35:36.439Z Has data issue: false hasContentIssue false
  • English
  • Français

INFINITE STRINGS AND THEIR LARGE SCALE PROPERTIES

Part of: Computability and recursion theory Discrete mathematics in relation to computer science Theory of computing

Published online by Cambridge University Press:  30 October 2020

BAKH KHOUSSAINOV  and
TORU TAKISAKA
BAKH KHOUSSAINOV
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF AUCKLAND PRIVATE BAG 92019, AUCKLAND, NEW ZEALANDE-mail: [email protected]: https://www.cs.auckland.ac.nz/~bmk/
TORU TAKISAKA
Affiliation:
INFORMATION SYSTEMS ARCHITECTURE SCIENCE RESEARCH DIVISION NATIONAL INSTITUTE OF INFORMATICS HITOTSUBASHI 2-1-2 TOKYO, JAPANE-mail: [email protected]: http://group-mmm.org/~toru/
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to shed light on our understanding of large scale properties of infinite strings. We say that one string 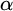$\alpha $ has weaker large scale geometry than that of 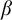$\beta $ if there is color preserving bi-Lipschitz map from 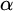$\alpha $ into 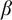$\beta $ with small distortion. This definition allows us to define a partially ordered set of large scale geometries on the classes of all infinite strings. This partial order compares large scale geometries of infinite strings. As such, it presents an algebraic tool for classification of global patterns. We study properties of this partial order. We prove, for instance, that this partial order has a greatest element and also possess infinite chains and antichains. We also investigate the sets of large scale geometries of strings accepted by finite state machines such as Büchi automata. We provide an algorithm that describes large scale geometries of strings accepted by Büchi automata. This connects the work with the complexity theory. We also prove that the quasi-isometry problem is a 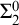$\Sigma _2^0$ -complete set, thus providing a bridge with computability theory. Finally, we build algebraic structures that are invariants of large scale geometries. We invoke asymptotic cones, a key concept in geometric group theory, defined via model-theoretic notion of ultra-product. Partly, we study asymptotic cones of algorithmically random strings, thus connecting the topic with algorithmic randomness.

Keywords

quasi-isometryBüchi automataultrafilterasymptotic conesΣ03-completenessalgorithmic randomness

MSC classification

Primary: 03D05: Automata and formal grammars in connection with logical questions
Secondary: 03D32: Algorithmic randomness and dimension 68Q45: Formal languages and automata 68Q70: Algebraic theory of languages and automata 68R15: Combinatorics on words
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 2 , June 2022 , pp. 585 - 625
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dioubina, A. and Polterovich, I., Structures at infinity of hyperbolic space (Russian) . Uspekhi Mat. Nauk , vol. 53 (1998), no. 5(323), pp. 239–240; translation in Russian Mathematical Surveys , vol. 53 (1998), no. 5, pp. 1093–1094.Google Scholar
Dioubina, A. and Polterovich, I., Explicit constructions of universal R-trees and asymptotic geometry of hyperbolic spaces . Bulletin of the London Mathematical Society , vol. 33 (2001), no. 6, pp. 727–734.10.1112/S002460930100844XCrossRefGoogle Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity , Springer-Verlag, New York, 2010.Google Scholar
Drutu, C. and Kapovich, M., Geometric Group Theory , Colloquium Publications, vol. 63, American Mathematical Society, Providence, RI, 2018.Google Scholar
Gromov, M., Groups of polynomial growth and expanding maps . Publications Mathématiques de l'Institut des Hautes Études Scientifiques , vol. 53 (1981), pp. 53–78.CrossRefGoogle Scholar
Gromov, M., Hyperbolic groups , Essays in Group Theory (Gersten, S. M., editor), M.S.R.I. Publications, vol. 8, Springer-Verlag, Berlin, Germany, 1987, pp. 75–263.10.1007/978-1-4613-9586-7_3CrossRefGoogle Scholar
Gromov, M., Asymptotic invariants of infinite groups, Geometric Group Theory (Niblo, G. A. and Roller, M. A., editors), London Mathematical Society, Lecture Notes Series, vol. 182, Cambridge University Press, Cambridge, 1993, pp. 1–295.Google Scholar
Jockusch, C. G. and Soare, R., ${\varPi}_1^0$ -classes and degrees of theories . Transactions of the American Mathematical Society , vol. 173 (1972), pp. 33–56.Google Scholar
Khoussainov, B. and Takisaka, T., Large scale geometries of infinite strings . Proceedings of the LICS (2017), pp. 1–12.Google Scholar
Lou, R., Quasi-isometric reductions between K-ary sequences , Bachelor thesis, National University of Singapore, 2019.Google Scholar
Nies, A., Computability and Randomness , Oxford University Press, Oxford, 2012.Google Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability , MIT Press, Cambridge, MA, 1987.Google Scholar
Van Den Dries, L. and Wilkie, A., On Gromov’s theorem concerning groups of polynomial growth and elementary logic . Journal of Algebra , vol. 89 (1984), pp. 349–374.10.1016/0021-8693(84)90223-0CrossRefGoogle Scholar
Velickovic, B. and Simon, T., Asymptotic cones of finitely generated groups . Bulletin of the London Mathematical Society , vol. 32 (2000), pp. 203–220.Google Scholar