Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T18:13:58.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitary properties of valued and ordered vector spaces

Published online by Cambridge University Press:  12 March 2014

Salma Kuhlmann
Salma Kuhlmann*
Affiliation:
The Fields Institute, 222, College Street, Toronto, Ontario, CanadaM5T 3J1, E-mail:, [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

§1. Introduction. The motivation of this work comes from two different directions: infinite abelian groups, and ordered algebraic structures. A challenging problem in both cases is that of classification. In the first case, it is known for example (cf. [KA]) that the classification of abelian torsion groups amounts to that of reduced p-groups by numerical invariants called the Ulm invariants (given by Ulm in [U]). Ulm's theorem was later generalized by P. Hill to the class of totally projective groups. As to the second case, let us consider for instance the class of divisible ordered abelian groups. These may be viewed as ordered ℚ-vector spaces. Their theory being unstable, we cannot hope to classify them by numerical invariants. On the other hand, being o-minimal, the theory enjoys several good model theoretic properties (cf. [P-S]), so the search for some reasonable invariants is well motivated. The common denominator of the two cases, as well as of many others, is valuation theory. Indeed given an ordered vector space, one can consider it as a valued vector space, endowed with the natural valuation. Also, the socle G[p] of a reduced abelian p-group G, endowed with the height function hG, is a valued vector space over 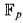(the prime field of characteristic p) with values in the ordinals (cf. [F]).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 1 , March 1999 , pp. 216 - 226
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BA]Barwise, J., Back and forth through infinitary logic, Studies in model theory (Morley, M., editor), Mathematical Association of America, Buffalo, NY, pp. 5–34.Google Scholar
[B-E]Barwise, J. and Eklof, P.C., Infinitary properties of abelian torsion groups, Annals of Mathematical Logic (1970), pp. 25–68.Google Scholar
[BR]Brown, R., Valued vector spaces of countable dimension, Universitatis Debreceniensis. Institutum Mathematicum. Publicationes Mathematicae, vol. 18 (1971), pp. 149–151.CrossRefGoogle Scholar
[E]Erdös, J., On the structure of ordered real vector spaces, Universitatis Debreceniensis. Institutum Mathematicum. Publicationes Mathematicae, vol. 4 (1955–1956), pp. 334–343.CrossRefGoogle Scholar
[F]Fuchs, L., Abelian p-groups and mixed groups, Montréal, 1980.Google Scholar
[H1]Hill, P., On the classification of abelian groups, photocopied manuscript, 1967.Google Scholar
[H2]Hill, P., On the classification of abelian groups, Abelian groups and modules, Proceedings of the conference in Udine 1984, CISM Courses Lectures, Springer, 1984, pp. 1–16.Google Scholar
[KA]Kaplansky, I., Infinite abelian groups, Ann Arbor, 1954.Google Scholar
[K-K]Kuhlmann, F.-V. and Kuhlmann, S., Ax–Kochen–Ershov principles for valued and ordered vector spaces, Ordered algebraic structures (Holland, W.C. and Martinez, J., editors), Kluwer Academic Publishers, 1997, pp. 237–259.CrossRefGoogle Scholar
[K1]Kuhlmann, S., On the structure of nonarchimedean exponential fields I, Archive for Mathematical Logic, vol. 34 (1995), pp. 145–182.CrossRefGoogle Scholar
[K2]Kuhlmann, S., Valuation bases for extensions of valued vector spaces, Forum Mathematicum, vol. 8 (1996), pp. 723–735.CrossRefGoogle Scholar
[P-S]Pillay, A. and Steinhorn, C., Definable sets in ordered structures I, Transactions of the American Mathematical Society, vol. 295 (1986), pp. 565–592.CrossRefGoogle Scholar
[PO]Poizat, B., Cours de théorie des modèles, Villeurbanne, 1985.Google Scholar
[R]Richman, F., Extensions of p-bounded groups, Archiv der Mathematik, vol. 21 (1970), pp. 449–454.CrossRefGoogle Scholar
[U]Ulm, H., Zur Theorie der abzählbar-unendlichen abelschen Gruppen, Mathematische Annalen, vol. 107 (1933), pp. 774–803.CrossRefGoogle Scholar