There are axiomatizations of the sentential calculus which, in effect, assert the inferential equivalence (mutual deducibility) of classes of sentences. A well known axiomatization of this sort consists of

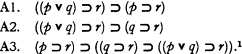
Another one, closely connected with A1–A3, is comprised of

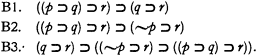
B1–B3 jointly assert the inferential equivalence of a sentence of the form (p ⊃ q) ⊃ r and two sentences of the forms q ⊃ r and ∼p ⊃ r respectively. This axiomatization requires the rule of substitution and the rule of detachment for conditionals.

The existence of such axiomatizations suggests a possibility of formulating natural deduction by means of inferential equivalence instead of the usual one-sided inference, customarily represented by ‘⊦’. ‘H’ will stand here for inferential equivalence. It may be looked upon as a combination of signs ‘⊦’ and ‘⊣’. ‘H’ is thought of as a metasystematic constant functor of two arguments each of which is a class of names of sentences. For purposes of this paper the first argument may be just a single name of a sentence, the second a pair (not necessarily ordered) of names of sentences. The role ‘H’ plays is determined by **1 –*5 below. Besides that ‘H’ remains here uninterpreted. In particular, it is not directly postulated that it is an identity relation.