Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T18:41:24.679Z Has data issue: false hasContentIssue false
  • English
  • Français

The independence of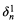

Published online by Cambridge University Press:  12 March 2014

Amir Leshem  and
Menachem Magidor
Amir Leshem
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel E-mail: [email protected]
Menachem Magidor
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove the independence of 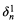for n ≥ 3. We show that 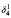can be forced to be above any ordinal of L using set forcing. For 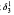we prove that it can be forced, using set forcing, to be above any L cardinal κ such that κ is Π1 definable without parameters in L. We then show that 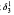cannot be forced by a set forcing to be above every cardinal of L Finally we present a class forcing construction to make 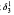greater than any given L cardinal.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 1 , March 1999 , pp. 350 - 362
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beller, A., Jensen, R. B., and Welch, P., Coding the universe, Cambridge University Press, 1982.CrossRefGoogle Scholar
[2]David, R., reals, Annals of Mathematical Logic, vol. 23 (1982), pp. 121–125.CrossRefGoogle Scholar
[3]David, R., A very absolute real singleton, Annals of Mathematical Logic, vol. 23 (1982), pp. 101–120.CrossRefGoogle Scholar
[4]Friedman, H., 102 problems in mathematical logic, this Journal, vol. 40 (1975), pp. 113–129.Google Scholar
[5]Harrington, L., The constructible reals can be (almost) everything, handwritten notes, 1977.Google Scholar
[6]Hinman, P. G., Recursion-theoretic hierarchies, Springer-Verlag, 1978.CrossRefGoogle Scholar
[7]Jech, T., Set theory, Academic Press, 1978.Google Scholar
[8]Jensen, R. B. and Solovay, R. M., Some applications of almost disjoint forcing, Mathematical logic and foundations of set theory (Bar-Hillel, Y., editor), Amsterdam, 1970.Google Scholar
[9]Kunen, K. and Tall, F. D., Between Martin's axiom and Souslin's hypothesis, Fundamenta Mathematicae vol. 102 (1979), pp. 173–181.CrossRefGoogle Scholar
[10]Moschovakis, Y. N., Descriptive set theory, Studies in Logic, vol. 100, North-Holland, 1980.Google Scholar