Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T09:21:01.437Z Has data issue: false hasContentIssue false
  • English
  • Français

INDEPENDENCE IN GENERIC INCIDENCE STRUCTURES

Published online by Cambridge University Press:  15 February 2019

GABRIEL CONANT  and
ALEX KRUCKMAN
GABRIEL CONANT
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN46556, USAE-mail: [email protected]
ALEX KRUCKMAN
Affiliation:
DEPARTMENT OF MATHEMATICS INDIANA UNIVERSITY BLOOMINGTON BLOOMINGTON, IN47405, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the theory Tm,n of existentially closed incidence structures omitting the complete incidence structure Km,n, which can also be viewed as existentially closed Km,n-free bipartite graphs. In the case m = n = 2, this is the theory of existentially closed projective planes. We give an 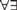$\forall \exists$-axiomatization of Tm,n, show that Tm,n does not have a countable saturated model when m, n ≥ 2, and show that the existence of a prime model for T2,2 is equivalent to a longstanding open question about finite projective planes. Finally, we analyze model theoretic notions of complexity for Tm,n. We show that Tm,n is NSOP1, but not simple when m, n ≥ 2, and we show that Tm,n has weak elimination of imaginaries but not full elimination of imaginaries. These results rely on combinatorial characterizations of various notions of independence, including algebraic independence, Kim independence, and forking independence.

Keywords

Primary 03C1003C4503C5251E1551E30Secondary 03C6551E30projective planesbipartite graphsNSOP1independence relationsforking
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 2 , June 2019 , pp. 750 - 780
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., A geometric introduction to forking and thorn-forking. Journal of Mathematical Logic, vol. 9 (2009), no. 1, pp. 1–20.Google Scholar
Baldwin, J. T., An almost strongly minimal non-Desarguesian projective plane. Transactions of the American Mathematical Society, vol. 342 (1994), no. 2, pp. 695–711.Google Scholar
Barbina, S. and Casanovas, E., Model theory of Steiner triple systems, 2018, arXiv:1805.06767.Google Scholar
Casanovas, E., Simple Theories and Hyperimaginaries, Lecture Notes in Logic, vol. 39, Cambridge University Press, Cambridge, 2011.Google Scholar
Chang, C. C. and Keisler, H. J., Model Theory. Studies in Logic and the Foundations of Mathematics, vol. 73, third ed., North-Holland, Amsterdam, 1990.Google Scholar
Chatzidakis, Z. and Pillay, A., Generic structures and simple theories. Annals of Pure and Applied Logic, vol. 95 (1998), no. 1–3, pp. 71–92.Google Scholar
Cherlin, G., Harrington, L., and Lachlan, A. H., .${\aleph _0}$-categorical, ${\aleph _0}$-stable structures. Annals of Pure and Applied Logic, vol. 28 (1985), no. 2, pp. 103–135.Google Scholar
Chernikov, A. and Ramsey, N., On model-theoretic tree properties. Journal of Mathematical Logic, vol. 16 (2016), no. 2, p. 1650009.Google Scholar
Conant, G., Forking and dividing in Henson graphs. Notre Dame Journal of Formal Logic, vol. 58 (2017), no. 4, pp. 555–566.Google Scholar
Conant, G. and Terry, C., Model theoretic properties of the Urysohn sphere. Annals of Pure and Applied Logic, vol. 167 (2016), no. 1, pp. 49–72.Google Scholar
Erdős, P., Some old and new problems in various branches of combinatorics, Proceedings of the Tenth Southeastern Conference on Combinatorics, Graph Theory and Computing (Florida Atlantic University Boca Raton, Fla., 1979) , Congressus Numerantium, XXIII–XXIV, Utilitas Mathematica, Winnipeg, 1979, pp. 19–37.Google Scholar
Hall, M., Projective planes. Transactions of the American Mathematical Society, vol. 54 (1943), pp. 229–277.Google Scholar
Henson, C. W., A family of countable homogeneous graphs. Pacific Journal of Mathematics, vol. 38 (1971), no. 1, pp. 69–83.Google Scholar
Hirschfeld, J. and Wheeler, W. H., Forcing, Arithmetic, Division Rings, Lecture Notes in Mathematics, vol. 454, Springer-Verlag, Berlin, 1975.Google Scholar
Hrushovski, E., Pseudofinite fields and related structures, Model Theory and Applications (Bélair, L., Chatzidakis, Z., D’Aquino, P., Marker, D., Otero, M., Point, F., and Wilkie, A., editors), Quaderni di Matematica, vol. 11, Aracne, Rome, 2002, pp. 151–212.Google Scholar
Kaplan, I. and Ramsey, N., On Kim-independence, 2017, arXiv:1702.03894.Google Scholar
Kegel, O. H., Existentially closed projective planes, Geometry—von Staudt’s Point of View (Plaumann, P. and Strambach, K., editors), Springer Netherlands, Dordrecht, 1981, pp. 165–174.Google Scholar
Kim, B. and Pillay, A., Simple theories. Annals of Pure and Applied Logic, vol. 88 (1997), no. 2–3, pp. 149–164. Joint AILA-KGS Model Theory Meeting (Florence, 1995).Google Scholar
Kruckman, A., Disjoint n-amalgamation and pseudofinite countably categorical theories, 2015, arXiv:1510.03539.Google Scholar
Kruckman, A. and Ramsey, N., Generic expansion and Skolemization in NSOP1 theories. Annals of Pure and Applied Logic, vol. 169 (2018), no. 8, pp. 755–774.Google Scholar
Montenegro, S. and Rideau, S., Imaginaries in pseudo p-adically closed fields, 2018, arXiv:1802.00256.Google Scholar
Moorhouse, G. E. and Williford, J., Embedding finite partial linear spaces in finite translation nets. Journal of Geometry, vol. 91 (2009), no. 1–2, pp. 73–83.Google Scholar
Saffe, J., A superstable theory with the dimensional order property has many models, Proceedings of the Herbrand Symposium (Marseilles, 1981) (Stern, J., editor), Studies in Logic and the Foundations of Mathematics, vol. 107, North-Holland, Amsterdam, 1982, pp. 281–286.Google Scholar
Shelah, S., Toward classifying unstable theories. Annals of Pure and Applied Logic, vol. 80 (1996), no. 3, pp. 229–255.Google Scholar
Tent, K. and Zilber, B., A non-desarguesian projective plane, 2012, arXiv:1510.06176.Google Scholar
Welsh, D. J. A., Matroid Theory, Academic Press [Harcourt Brace Jovanovich], London-New York, 1976.Google Scholar