Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T02:11:57.352Z Has data issue: false hasContentIssue false
  • English
  • Français

Increasing u2 by a stationary set preserving forcing

Published online by Cambridge University Press:  12 March 2014

Benjamin Claverie  and
Ralf Schindler
Benjamin Claverie
Affiliation:
Institut für Mathematische Logik und Grundlagenforschung, Universität Münster, Einsteinstr. 62, 48149 Münster, Germany, E-mail: [email protected], E-mail: [email protected]
Ralf Schindler
Affiliation:
Institut für Mathematische Logik und Grundlagenforschung, Universität Münster, Einsteinstr. 62, 48149 Münster, Germany, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if I is a precipitous ideal on ω1 and if θ > ω1 is a regular cardinal, then there is a forcing ℙ = ℙ(I, θ) which preserves the stationarity of all I-positive sets such that in Vℙ, ⟨Hθ; ∈, I⟩ is a generic iterate of a countable structure ⟨M; ∈, Ī⟩. This shows that if the nonstationary ideal on ω1 is precipitous and 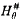exists, then there is a stationary set preserving forcing which increases 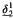. Moreover, if Bounded Martin's Maximum holds and the nonstationary ideal on ω1 is precipitous, then .

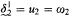Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 1 , March 2009 , pp. 187 - 200
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[FS88]Foreman, Matthew, Magidor, Menachem, and Shelah, Saharon, Martin's Maximum, Saturated Ideals, and Nonregular Ultrafilters. Part I, Annals of Mathematics, vol. 127 (1988), no. 1, pp. 1–47.CrossRefGoogle Scholar
[Jec03]Jech, Thomas, Set theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003, The third millennium edition, revised and expanded.Google Scholar
[Jen90a]Jensen, Ronald, Making cardinals ω-cofinal, 1990, Handwritten notes, available at http://www-irm.mathematik.hu-berlin.de/~raesch/org/jensen/pdf/Making-Cards.pdf.Google Scholar
[Jen90b[Jensen, Ronald, On some problems of Mitchell, Welch and Vickers, 1990, Handwritten notes, available at http://www-irm.mathematik.hu-berlin.de/~raesch/org/jensen/pdf/Some-Problems. pdf.Google Scholar
[KLZ07[Ketchersid, Richard, Larson, Paul, and Zapletal, Jindřich, Increasing and Namba style forcing, this Journal, vol. 72 (2007), no. 4, pp. 1372–1387.Google Scholar
[Mos80[Moschovakis, Yiannis, Descriptive set theory, North Holland Publishing Company, Amsterdam, New York, Oxford, 1980.Google Scholar
[Sch04[Schindler, Ralf, Semi-proper forcing, remarkable cardinals, and Bounded Martin's Maximum, Mathematical Logic Quarterly, vol. 50 (2004), no. 6, pp. 527–32.CrossRefGoogle Scholar
[SVW82[Steel, John R. and Van Wesep, Robert, Two consequences of determinacy consistent with choice, Transactions of the American Mathematical Society, vol. 272 (1982), no. 1, pp. 67–85.CrossRefGoogle Scholar
[Woo99[Woodin, W. Hugh, The axiom of determinacy, forcing axioms, and the nonstationary ideal, de Gruyter Series in Logic and its Applications, vol. 1, Walter de Gruyter & Co., Berlin, 1999.CrossRefGoogle Scholar