Article contents
The inconsistency of 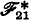
Published online by Cambridge University Press: 12 March 2014
Extract
In [4] Curry raised the possibility that his system 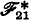 proposed in ξ15C of [3] might be inconsistent. In this paper this inconsistency is proved using a method also employed in [1].
proposed in ξ15C of [3] might be inconsistent. In this paper this inconsistency is proved using a method also employed in [1].
From Curry's axiom ⊦LH, it follows that

holds for arbitrary X.
The other results from 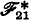 that are required are
that are required are
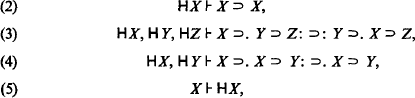
Modus Ponens, and the Deduction Theorem for implication:
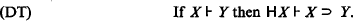
Assuming ⊦HA, we define as in [1]:
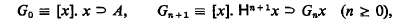
and let
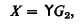
where Y is the paradoxical (or fixed point) combinator.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
References
REFERENCES
- 2
- Cited by


