Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T04:24:18.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypermachines

Published online by Cambridge University Press:  12 March 2014

Sy-David Friedman  and
P. D. Welch
Sy-David Friedman
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, Währingerstraβe 25, 1090 Vienna, Austria, E-mail: [email protected]
P. D. Welch
Affiliation:
School of Mathematics, University of Bristol, Bristol, BS8 1TW, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Infinite Time Turing Machine model [8] of Hamkins and Kidder is, in an essential sense, a “Σ2-machine” in that it uses a Σ2Liminf Rule to determine cell values at limit stages of time. We give a generalisation of these machines with an appropriate Σn rule. Such machines either halt or enter an infinite loop by stage 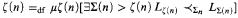, again generalising precisely the ITTM case.

The collection of such machines taken together computes precisely those reals of the least model of analysis.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 620 - 636
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Burgess, J. P., The truth is never simple, this Journal, vol. 51 (1986), no. 3, pp. 663–681.Google Scholar
[2]Devlin, K., Constructibility, Perspectives in Mathematical Logic, Springer Verlag, Berlin and Heidelberg, 1984.CrossRefGoogle Scholar
[3]Feng, Q. and Jensen, R. B., Supercomplete extenders and type-1 mice, Annals of Pure and Applied Logic, vol. 126 (2004), no. 1–3, pp. 1–73.CrossRefGoogle Scholar
[4]Field, H., Saving truth from paradox, Oxford University Press, 2008.CrossRefGoogle Scholar
[5]Friedman, S. D., Fine structure and class forcing, Series in Logic and its Applications, vol. 3, de Gruyter, Berlin and New York, 2000.CrossRefGoogle Scholar
[6]Friedman, S. D., Parameter free uniformisation, Proceedings of the American Mathematical Society, vol. 136 (2008), pp. 3327–3330.CrossRefGoogle Scholar
[7]Friedman, S. D. and Welch, P. D., Two observations concerning infinite time Turing machines, Bonn International Workshop on Ordinal Computability (BIWOC 2007 Bonn) (Dimitriou, I., editor), Hausdorff Centre for Mathematics, 01 2007, also at http://www.logic.univie.ac.at/sdf/papers/joint.philip.ps, pp. 44–47.Google Scholar
[8]Hamkins, J. D. and Lewis, A., Infinite time Turing machines, this Journal, vol. 65 (2000), no. 2, pp. 567–604.Google Scholar
[9]Jensen, R. B., The fine structure of the constructible hierarchy, Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308.CrossRefGoogle Scholar
[10]Kanamori, A., The higher infinite, Omega Series in Logic, Springer Verlag, New York, 1994.Google Scholar
[11]Kechris, A., Homogenous trees and projective scales. Cabal seminar 77–79: Proceedings of the Caltech-UCLA logic seminar 1977–1979 (Martin, D. A., Kechris, A., and Moschovakis, Y., editors), Lecture Notes in Mathematics, vol. 839, Springer, Berlin, 1981, pp. 33–73.CrossRefGoogle Scholar
[12]Moschovakis, Y. N., Descriptive set theory, Studies in Logic, North-Holland, Amsterdam, 1980.Google Scholar
[13]Sacks, G. E., The 1-section of a type-k object, Proceedings of the 1972 Oslo symposium (Fenstad, J. E. and Hinman, P. G., editors), Studies in Logic, North-Holland, Amsterdam, 1974, pp. 81–93.Google Scholar
[14]Welch, P. D., Eventually Infinite Time Turing degrees: infinite time decidable reals, this Journal, vol. 65 (2000), no. 3, pp. 1193–1203.Google Scholar
[15]Welch, P. D., Characteristics of discrete transfinite Turing machine models: halting times, stabilization times, and normal form theorems, Theoretical Computer Science, vol. 410 (2009), pp. 426–442.CrossRefGoogle Scholar
[16]Welch, P. D., Determinacy in strong cardinal models, this Journal, (submitted).Google Scholar
[17]Welch, P. D., Weak systems of determinacy and arithmetical quasi-inductive definitions, this Journal, (to appear), arXiv:0905.4412.Google Scholar