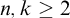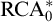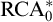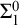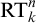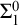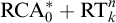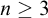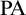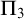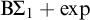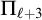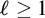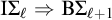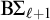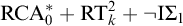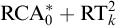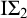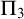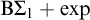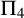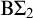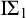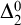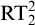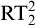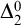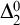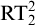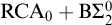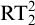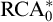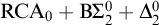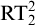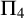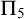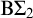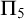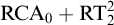Over the last two decades, much of the research in reverse mathematics has concerned the logical strength of various principles from Ramsey theory. One of the challenging problems in this area has been to characterize the first-order consequences of Ramsey’s Theorem for pairs. Despite significant progress (e.g., [Reference Cholak, Jockusch and Slaman4, Reference Chong, Slaman and Yang7, Reference Patey and Yokoyama27]), this remains open. In particular, it is not known whether Ramsey’s Theorem for pairs and a fixed number of colours is
![]() $\Pi ^1_1$
conservative over the
$\Pi ^1_1$
conservative over the
![]() $\Sigma ^0_2$
collection scheme.
$\Sigma ^0_2$
collection scheme.
In this paper, we study the first-order strength of Ramsey’s Theorem—both for pairs and for longer tuples of fixed length—over a weaker base theory than the one normally used in reverse mathematics. Our base theory,
![]() $\mathrm {RCA}^*_0$
, differs from the usual system
$\mathrm {RCA}^*_0$
, differs from the usual system
![]() $\mathrm {RCA}_0$
in that the
$\mathrm {RCA}_0$
in that the
![]() $\Sigma ^0_1$
induction axiom of the latter is replaced by induction for bounded formulas only.
$\Sigma ^0_1$
induction axiom of the latter is replaced by induction for bounded formulas only.
The study of
![]() $\mathrm {RCA}^*_0$
was initiated in [Reference Simpson and Smith31] and continued in a number of later papers, e.g., [Reference Enayat and Wong10, Reference Hatzikiriakou14, Reference Kołodziejczyk and Yokoyama21, Reference Simpson and Yokoyama32]. In the context of Ramsey theory, it is important that
$\mathrm {RCA}^*_0$
was initiated in [Reference Simpson and Smith31] and continued in a number of later papers, e.g., [Reference Enayat and Wong10, Reference Hatzikiriakou14, Reference Kołodziejczyk and Yokoyama21, Reference Simpson and Yokoyama32]. In the context of Ramsey theory, it is important that
![]() $\Sigma ^0_1$
induction is needed to show that each infinite set has arbitrarily large finite subsets. Hence, over
$\Sigma ^0_1$
induction is needed to show that each infinite set has arbitrarily large finite subsets. Hence, over
![]() $\mathrm {RCA}^*_0$
the infinite homogeneous sets witnessing various principles might be so sparse that they have “strictly smaller cardinality” than
$\mathrm {RCA}^*_0$
the infinite homogeneous sets witnessing various principles might be so sparse that they have “strictly smaller cardinality” than
![]() $\mathbb {N}$
, so the principles can become weaker. Indeed, the third author [Reference Yokoyama34] showed that for each fixed
$\mathbb {N}$
, so the principles can become weaker. Indeed, the third author [Reference Yokoyama34] showed that for each fixed
![]() $n,k$
,
$n,k$
,
![]() $\mathrm {RCA}^*_0$
extended by Ramsey’s Theorem for n-tuples and k colours,
$\mathrm {RCA}^*_0$
extended by Ramsey’s Theorem for n-tuples and k colours,
![]() $\mathrm {RT}^n_k$
, is
$\mathrm {RT}^n_k$
, is
![]() $\Pi _2$
-conservative over
$\Pi _2$
-conservative over
![]() $\mathrm {I}\Delta _0 + \exp $
. We are able to go quite a bit beyond that result.
$\mathrm {I}\Delta _0 + \exp $
. We are able to go quite a bit beyond that result.
Recent work of Belanger [Reference Belanger3] has demonstrated that the study of reverse mathematics over
![]() $\mathrm {RCA}^*_0$
is relevant to the traditional
$\mathrm {RCA}^*_0$
is relevant to the traditional
![]() $\mathrm {RCA}_0$
framework as well. In fact, a large part of our original motivation for studying Ramsey’s Theorem over
$\mathrm {RCA}_0$
framework as well. In fact, a large part of our original motivation for studying Ramsey’s Theorem over
![]() $\mathrm {RCA}^*_0$
was the desire to understand whether it can help in understanding
$\mathrm {RCA}^*_0$
was the desire to understand whether it can help in understanding
![]() $\mathrm {RT}^2_2$
over
$\mathrm {RT}^2_2$
over
![]() $\mathrm {RCA}_0$
. The jury is still out on that. However, it has turned out that Ramsey theory in
$\mathrm {RCA}_0$
. The jury is still out on that. However, it has turned out that Ramsey theory in
![]() $\mathrm {RCA}^*_0$
is a highly interesting topic in its own right. It gives rise to new examples of principles that are partially conservative but not
$\mathrm {RCA}^*_0$
is a highly interesting topic in its own right. It gives rise to new examples of principles that are partially conservative but not
![]() $\Pi ^1_1$
-conservative over the base theory, and it has intriguing connections to the model theory of first-order arithmetic.
$\Pi ^1_1$
-conservative over the base theory, and it has intriguing connections to the model theory of first-order arithmetic.
After discussing the necessary background in a preliminary Section 1, we begin the paper proper in Section 2 by proving that in models of
![]() $\mathrm {RCA}^*_0$
that are not models of
$\mathrm {RCA}^*_0$
that are not models of
![]() $\mathrm {RCA}_0$
,
$\mathrm {RCA}_0$
,
![]() $\mathrm {RT}^n_k$
is equivalent to its relativizations to
$\mathrm {RT}^n_k$
is equivalent to its relativizations to
![]() $\Sigma ^0_1$
-definable cuts. One consequence of that result is that in some models of
$\Sigma ^0_1$
-definable cuts. One consequence of that result is that in some models of
![]() $\mathrm {RCA}^*_0$
, Ramsey’s Theorem is computably true. This is not the case in the standard model of arithmetic or in any other model of
$\mathrm {RCA}^*_0$
, Ramsey’s Theorem is computably true. This is not the case in the standard model of arithmetic or in any other model of
![]() $\mathrm {RCA}_0$
.
$\mathrm {RCA}_0$
.
In Section 3, we use the equivalence from Section 2 to give an axiomatization of the first-order consequences of
![]() $\mathrm {RCA}^*_0 +\mathrm {RT}^n_k$
where
$\mathrm {RCA}^*_0 +\mathrm {RT}^n_k$
where
![]() $n \ge 3$
. In each case, this turns out to be an unusual fragment of Peano Arithmetic that is
$n \ge 3$
. In each case, this turns out to be an unusual fragment of Peano Arithmetic that is
![]() $\Pi _3$
- but not
$\Pi _3$
- but not
![]() $\Pi _4$
-conservative over
$\Pi _4$
-conservative over
![]() $\mathrm {B}\Sigma _1+\exp $
. Moreover, it is not contained in
$\mathrm {B}\Sigma _1+\exp $
. Moreover, it is not contained in
![]() $\mathrm {I} \Sigma _\ell $
for any
$\mathrm {I} \Sigma _\ell $
for any
![]() $\ell $
.
$\ell $
.
We then consider Ramsey’s Theorem for pairs. We are not able to give a complete axiomatization of its first-order consequences over
![]() $\mathrm {RCA}^*_0$
, but in Section 4 we obtain some partial results. In particular, we do axiomatize these consequences over
$\mathrm {RCA}^*_0$
, but in Section 4 we obtain some partial results. In particular, we do axiomatize these consequences over
![]() $\neg \mathrm {I}\Sigma _1$
. We also show that
$\neg \mathrm {I}\Sigma _1$
. We also show that
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
is not conservative over (the lightface theory)
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
is not conservative over (the lightface theory)
![]() $\mathrm {I}\Sigma _1$
.
$\mathrm {I}\Sigma _1$
.
Then, in Section 5, we take a look at the question whether our results say anything about Ramsey’s Theorem for pairs over
![]() $\mathrm {RCA}_0$
. We consider a principle that can be viewed as a “jumped version” of
$\mathrm {RCA}_0$
. We consider a principle that can be viewed as a “jumped version” of
![]() $\mathrm {RT}^2_2$
, and we show that it is not
$\mathrm {RT}^2_2$
, and we show that it is not
![]() $\Pi _5$
-conservative over
$\Pi _5$
-conservative over
![]() $\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$
. We also show that the most obvious sentence witnessing the lack of conservativity is unprovable in
$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$
. We also show that the most obvious sentence witnessing the lack of conservativity is unprovable in
![]() $\mathrm {RCA}_0 +\mathrm {RT}^2_2$
. However, the proof of unprovability, which is based on a possibly unexpected technique (proof speedup), no longer works for slightly weaker sentences.
$\mathrm {RCA}_0 +\mathrm {RT}^2_2$
. However, the proof of unprovability, which is based on a possibly unexpected technique (proof speedup), no longer works for slightly weaker sentences.
1 Preliminaries
We assume that the reader has some familiarity with fragments of second-order arithmetic, as described in [Reference Simpson30] or [Reference Hirschfeldt15]. We also assume familiarity with some basic facts about first-order arithmetic and its models—most or all of the necessary information can be found in [Reference Hirschfeldt15], and [Reference Kaye18] covers more than enough.
The symbol
![]() $\omega $
stands for the set of standard natural numbers. In contrast,
$\omega $
stands for the set of standard natural numbers. In contrast,
![]() $\mathbb {N}$
stands for the set of natural numbers as formalized in the given theory we are studying—in a nonstandard model, this is the first-order universe of the model.
$\mathbb {N}$
stands for the set of natural numbers as formalized in the given theory we are studying—in a nonstandard model, this is the first-order universe of the model.
Notation like
![]() $\Sigma ^0_\ell $
,
$\Sigma ^0_\ell $
,
![]() $\Pi ^0_\ell $
represents the usual formula classes defined in terms of first-order quantifier alternations, but allowing second-order free variables. On the other hand, notation without the superscript
$\Pi ^0_\ell $
represents the usual formula classes defined in terms of first-order quantifier alternations, but allowing second-order free variables. On the other hand, notation without the superscript
![]() $0$
, like
$0$
, like
![]() $\Sigma _\ell $
,
$\Sigma _\ell $
,
![]() $\Pi _\ell $
, represents analogously defined classes of first-order, or “lightface,” formulas—that is, without any second-order variables at all. If we want to specify the second-order parameters appearing in a
$\Pi _\ell $
, represents analogously defined classes of first-order, or “lightface,” formulas—that is, without any second-order variables at all. If we want to specify the second-order parameters appearing in a
![]() $\Sigma ^0_\ell $
formula, we use notation like
$\Sigma ^0_\ell $
formula, we use notation like
![]() $\Sigma _\ell (\bar X)$
. We extend these conventions to naming theories: thus, for example,
$\Sigma _\ell (\bar X)$
. We extend these conventions to naming theories: thus, for example,
![]() $\mathrm {B}\Sigma ^0_2$
is the fragment of second-order arithmetic axiomatized by
$\mathrm {B}\Sigma ^0_2$
is the fragment of second-order arithmetic axiomatized by
![]() $\Delta ^0_0$
induction and
$\Delta ^0_0$
induction and
![]() $\Sigma ^0_2$
collection, whereas
$\Sigma ^0_2$
collection, whereas
![]() $\mathrm {B}\Sigma _2$
is the fragment of first-order arithmetic axiomatized by
$\mathrm {B}\Sigma _2$
is the fragment of first-order arithmetic axiomatized by
![]() $\Delta _0$
induction and
$\Delta _0$
induction and
![]() $\Sigma _2$
collection. (We follow the custom of some other authors in assuming also that all theories
$\Sigma _2$
collection. (We follow the custom of some other authors in assuming also that all theories
![]() $\mathrm {I} \Sigma _\ell $
,
$\mathrm {I} \Sigma _\ell $
,
![]() $\mathrm {B} \Sigma _\ell $
, etc. contain
$\mathrm {B} \Sigma _\ell $
, etc. contain
![]() $\mathrm {PA}^-$
, the theory of nonnegative parts of discretely ordered rings.)
$\mathrm {PA}^-$
, the theory of nonnegative parts of discretely ordered rings.)
Remark. In formulating the results presented in the paper, we had to make the decision whether to state them in purely arithmetical, lightface, form, or in
![]() $\Pi ^1_1$
form, allowing the appearance of (typically universally quantified) second-order parameters. We opted to use the lightface version most of the time, with the tacit understanding that our results of the form “first-order scheme T implies first-order sentence
$\Pi ^1_1$
form, allowing the appearance of (typically universally quantified) second-order parameters. We opted to use the lightface version most of the time, with the tacit understanding that our results of the form “first-order scheme T implies first-order sentence
![]() $\psi $
” (as for instance Lemma 3.3) typically have a natural relativization of the form “for all X,
$\psi $
” (as for instance Lemma 3.3) typically have a natural relativization of the form “for all X,
![]() $T(X)$
implies
$T(X)$
implies
![]() $\psi (X)$
” that can be proved by essentially the same argument. On the other hand, we did allow second-order parameters whenever we found it advisable, for instance because it was necessary to state the result properly (as in Theorem 4.3) or needed for later applications (as in the case of Theorem 2.3).
$\psi (X)$
” that can be proved by essentially the same argument. On the other hand, we did allow second-order parameters whenever we found it advisable, for instance because it was necessary to state the result properly (as in Theorem 4.3) or needed for later applications (as in the case of Theorem 2.3).
Recall that for
![]() $\ell \ge 1$
the theory
$\ell \ge 1$
the theory
![]() $\mathrm {I}\Sigma _\ell $
proves (in fact, is equivalent to over
$\mathrm {I}\Sigma _\ell $
proves (in fact, is equivalent to over
![]() $\mathrm {I} \Delta _0$
) the scheme of strong
$\mathrm {I} \Delta _0$
) the scheme of strong
![]() $\Sigma _\ell $
collection, that is,
$\Sigma _\ell $
collection, that is,
where
![]() $\sigma (x,y)$
is a
$\sigma (x,y)$
is a
![]() $\Sigma _\ell $
formula, possibly with parameters.
$\Sigma _\ell $
formula, possibly with parameters.
The theory
![]() $\mathrm {RCA}^*_0$
is obtained from
$\mathrm {RCA}^*_0$
is obtained from
![]() $\mathrm {RCA}_0$
by weakening the
$\mathrm {RCA}_0$
by weakening the
![]() $\mathrm {I}\Sigma ^0_1$
axiom to
$\mathrm {I}\Sigma ^0_1$
axiom to
![]() $\mathrm {B}\Sigma ^0_1$
and adding the axiom
$\mathrm {B}\Sigma ^0_1$
and adding the axiom
![]() $\exp $
that explicitly guarantees the totality of exponentiation. The first-order consequences of
$\exp $
that explicitly guarantees the totality of exponentiation. The first-order consequences of
![]() $\mathrm {RCA}^*_0$
are axiomatized by
$\mathrm {RCA}^*_0$
are axiomatized by
![]() $\mathrm {B}\Sigma _1 + \exp $
.
$\mathrm {B}\Sigma _1 + \exp $
.
When we consider a model
![]() $(M,\mathcal {X})$
of some fragment of second-order arithmetic (or simply work inside this fragment without reference to a specific model), a set is an element of the second-order universe, i.e., an element of
$(M,\mathcal {X})$
of some fragment of second-order arithmetic (or simply work inside this fragment without reference to a specific model), a set is an element of the second-order universe, i.e., an element of
![]() $\mathcal {X}$
. In contrast, a definable set is any subset of M that is definable in
$\mathcal {X}$
. In contrast, a definable set is any subset of M that is definable in
![]() $(M,\mathcal {X})$
, but does not have to belong to
$(M,\mathcal {X})$
, but does not have to belong to
![]() $\mathcal {X}$
. A definable set is a
$\mathcal {X}$
. A definable set is a
![]() $\Delta ^0_\ell $
-definable set, or simply a
$\Delta ^0_\ell $
-definable set, or simply a
![]() $\Delta ^0_\ell $
-set (resp. a
$\Delta ^0_\ell $
-set (resp. a
![]() $\Sigma ^0_\ell $
-definable set or
$\Sigma ^0_\ell $
-definable set or
![]() $\Sigma ^0_\ell $
-set) if it happens to be definable by a
$\Sigma ^0_\ell $
-set) if it happens to be definable by a
![]() $\Delta ^0_\ell $
(resp.
$\Delta ^0_\ell $
(resp.
![]() $\Sigma ^0_{\ell}$
) formula. The notions of a
$\Sigma ^0_{\ell}$
) formula. The notions of a
![]() $\Delta _\ell $
-set and
$\Delta _\ell $
-set and
![]() $\Sigma _\ell $
-set are defined analogously.
$\Sigma _\ell $
-set are defined analogously.
Since most of the models we study only satisfy
![]() $\Delta ^0_1$
-comprehension,
$\Delta ^0_1$
-comprehension,
![]() $\Delta ^0_\ell $
-sets for
$\Delta ^0_\ell $
-sets for
![]() $\ell \ge 2$
and
$\ell \ge 2$
and
![]() $\Sigma ^0_\ell $
-sets for
$\Sigma ^0_\ell $
-sets for
![]() $\ell \ge 1$
will not always be sets. However, using appropriate universal formulas, we can quantify over
$\ell \ge 1$
will not always be sets. However, using appropriate universal formulas, we can quantify over
![]() $\Delta ^0_\ell $
- or over
$\Delta ^0_\ell $
- or over
![]() $\Sigma ^0_\ell $
-sets using second-order quantifiers (e.g., “for every X, and every equivalent pair of a
$\Sigma ^0_\ell $
-sets using second-order quantifiers (e.g., “for every X, and every equivalent pair of a
![]() $\Sigma ^0_\ell (X)$
and a
$\Sigma ^0_\ell (X)$
and a
![]() $\Pi ^0_\ell (X)$
formula,
$\Pi ^0_\ell (X)$
formula,
![]() $\ldots $
”). On the other hand, quantification over
$\ldots $
”). On the other hand, quantification over
![]() $\Delta _\ell $
- or over
$\Delta _\ell $
- or over
![]() $\Sigma _\ell $
-sets is first-order. We write
$\Sigma _\ell $
-sets is first-order. We write
![]() $\Delta _{\ell }$
-
$\Delta _{\ell }$
-
![]() $\mathrm {Def}(M)$
(resp.
$\mathrm {Def}(M)$
(resp.
![]() $\Delta ^0_{\ell }$
-
$\Delta ^0_{\ell }$
-
![]() $\mathrm {Def}(M,\mathcal {X})$
) for the collection of
$\mathrm {Def}(M,\mathcal {X})$
) for the collection of
![]() $\Delta _\ell $
-definable subsets of M (resp. the subsets of M that are
$\Delta _\ell $
-definable subsets of M (resp. the subsets of M that are
![]() $\Delta ^0_\ell $
-definable in
$\Delta ^0_\ell $
-definable in
![]() $(M,\mathcal {X})$
).
$(M,\mathcal {X})$
).
For
![]() $\ell \ge 1$
, let
$\ell \ge 1$
, let
![]() $\mathrm {Sat}_\ell (x,y)$
be the usual universal
$\mathrm {Sat}_\ell (x,y)$
be the usual universal
![]() $\Sigma _\ell $
formula and let
$\Sigma _\ell $
formula and let
![]() $\mathrm {Sat}_\ell (x,y,X)$
be the usual universal
$\mathrm {Sat}_\ell (x,y,X)$
be the usual universal
![]() $\Sigma ^0_\ell $
formula with the unique second-order variable X. Then
$\Sigma ^0_\ell $
formula with the unique second-order variable X. Then
![]() $0^{(\ell )}$
is the
$0^{(\ell )}$
is the
![]() $\Sigma _\ell $
definable set
$\Sigma _\ell $
definable set
![]() $\{e: \mathrm {Sat}_\ell (e,e)\}$
; we write
$\{e: \mathrm {Sat}_\ell (e,e)\}$
; we write
![]() $0'$
for
$0'$
for
![]() $0^{(1)}$
. Similarly, if A is a set, then
$0^{(1)}$
. Similarly, if A is a set, then
![]() $A^{(\ell )}$
is
$A^{(\ell )}$
is
![]() $\{e: \mathrm {Sat}_\ell (e,e,A)\}$
; this notion is generalized in a natural way to the case where A is merely a definable set. Note that
$\{e: \mathrm {Sat}_\ell (e,e,A)\}$
; this notion is generalized in a natural way to the case where A is merely a definable set. Note that
![]() $\mathrm {B} \Sigma _\ell $
is enough to prove that
$\mathrm {B} \Sigma _\ell $
is enough to prove that
![]() $0^{(\ell +1)}$
and
$0^{(\ell +1)}$
and
![]() $(0^{(\ell )})'$
are mutually
$(0^{(\ell )})'$
are mutually
![]() $\Delta _1$
-definable.
$\Delta _1$
-definable.
For
![]() $n,k \in \omega $
,
$n,k \in \omega $
,
![]() $\mathrm {RT}^n_k$
stands for the usual formulation of Ramsey’s Theorem for n-tuples in second-order arithmetic: “for every function
$\mathrm {RT}^n_k$
stands for the usual formulation of Ramsey’s Theorem for n-tuples in second-order arithmetic: “for every function
![]() $f \colon [\mathbb {N}]^n \to k$
, there is an infinite homogeneous set H for f.” Importantly, “H is infinite” is understood here as “H is unbounded,” i.e., for every
$f \colon [\mathbb {N}]^n \to k$
, there is an infinite homogeneous set H for f.” Importantly, “H is infinite” is understood here as “H is unbounded,” i.e., for every
![]() $x \in \mathbb {N}$
there is
$x \in \mathbb {N}$
there is
![]() $H \ni y \ge x$
. If
$H \ni y \ge x$
. If
![]() $\Sigma ^0_1$
induction fails, this does not imply that H contains an x-element finite subset for every x. Ramsey’s Theorem formulated in terms of the latter notion is easily seen to imply
$\Sigma ^0_1$
induction fails, this does not imply that H contains an x-element finite subset for every x. Ramsey’s Theorem formulated in terms of the latter notion is easily seen to imply
![]() $\mathrm {I} \Sigma ^0_1$
[Reference Yokoyama34].
$\mathrm {I} \Sigma ^0_1$
[Reference Yokoyama34].
A cut in a model of arithmetic M is any subset
![]() $I \subseteq M$
which contains
$I \subseteq M$
which contains
![]() $0$
and is closed downwards and under successor; note that if
$0$
and is closed downwards and under successor; note that if
![]() $I \neq M$
, it will never be a “set” in the sense of belonging to whatever second-order arithmetic structure there might be on M. A definable cut is a cut that happens to be a definable set. If
$I \neq M$
, it will never be a “set” in the sense of belonging to whatever second-order arithmetic structure there might be on M. A definable cut is a cut that happens to be a definable set. If
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0$
, and I is a
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0$
, and I is a
![]() $\Sigma ^0_1$
-definable cut in M, then there is an infinite set
$\Sigma ^0_1$
-definable cut in M, then there is an infinite set
![]() $A \in \mathcal {X}$
of cardinality I, i.e.,
$A \in \mathcal {X}$
of cardinality I, i.e.,
![]() $A = \{a_i: i \in I\}$
enumerated in increasing order.
$A = \{a_i: i \in I\}$
enumerated in increasing order.
For an element s of a model M,
![]() $(s)_{\mathrm {Ack}}$
stands for
$(s)_{\mathrm {Ack}}$
stands for
![]() $\{a \in M: M \models a \in _{\mathrm {Ack}} s\}$
, where
$\{a \in M: M \models a \in _{\mathrm {Ack}} s\}$
, where
![]() $\in _{\mathrm {Ack}}$
is the usual Ackermann interpretation of set theory in arithmetic (“the a-th bit in the binary notation for s is 1”). Given a proper cut
$\in _{\mathrm {Ack}}$
is the usual Ackermann interpretation of set theory in arithmetic (“the a-th bit in the binary notation for s is 1”). Given a proper cut
![]() $I \subseteq M$
, the collection
$I \subseteq M$
, the collection
![]() $\mathrm {Cod}(M/I)$
of subsets of I coded in M is
$\mathrm {Cod}(M/I)$
of subsets of I coded in M is
![]() $\{(s)_{\mathrm {Ack}} \cap I: s \in M\}$
. If M satisfies induction for any of the classes of formulas
$\{(s)_{\mathrm {Ack}} \cap I: s \in M\}$
. If M satisfies induction for any of the classes of formulas
![]() $\Gamma $
that we consider in this paper, this will coincide with
$\Gamma $
that we consider in this paper, this will coincide with
![]() $\{A \cap I: A \textrm { a } \Gamma \textrm {-definable subset of } M\}$
.
$\{A \cap I: A \textrm { a } \Gamma \textrm {-definable subset of } M\}$
.
The collection
![]() $\mathrm {Cod}(M/\omega )$
is commonly referred to as the standard system of M and denoted by
$\mathrm {Cod}(M/\omega )$
is commonly referred to as the standard system of M and denoted by
![]() $\mathrm {SSy}(M)$
. The following combination of standard model-theoretic facts discussed in [Reference Kaye18] and well-known results on
$\mathrm {SSy}(M)$
. The following combination of standard model-theoretic facts discussed in [Reference Kaye18] and well-known results on
![]() $\mathrm {RT}^n_k$
presented, e.g., in [Reference Hirschfeldt15] will often be used without notice, for instance in the proof of Theorem 3.7.
$\mathrm {RT}^n_k$
presented, e.g., in [Reference Hirschfeldt15] will often be used without notice, for instance in the proof of Theorem 3.7.
Fact. Let
![]() $\mathcal {S} \subseteq \mathcal {P}(\omega )$
be such that
$\mathcal {S} \subseteq \mathcal {P}(\omega )$
be such that
![]() $(\omega , \mathcal {S}) \models \mathrm {WKL}_0$
(such a family
$(\omega , \mathcal {S}) \models \mathrm {WKL}_0$
(such a family
![]() $\mathcal {S}$
is known as a Scott set). If
$\mathcal {S}$
is known as a Scott set). If
![]() $\mathcal {S}$
is countable, then for every consistent computably axiomatized theory
$\mathcal {S}$
is countable, then for every consistent computably axiomatized theory
![]() $T \supseteq \mathrm {I} \Delta _0 + \exp $
there exists a model
$T \supseteq \mathrm {I} \Delta _0 + \exp $
there exists a model
![]() $M\models T$
such that
$M\models T$
such that
![]() $\mathrm {SSy}(M)=\mathcal {S}$
, and for every
$\mathrm {SSy}(M)=\mathcal {S}$
, and for every
![]() $\ell \ge 1$
there exists
$\ell \ge 1$
there exists
![]() $M\models \mathrm {B}\Sigma _{\ell }$
such that
$M\models \mathrm {B}\Sigma _{\ell }$
such that
![]() $\omega $
is
$\omega $
is
![]() $\Sigma _{\ell }$
-definable in M and
$\Sigma _{\ell }$
-definable in M and
![]() $\mathrm {SSy}(M)=\mathcal {S}$
.
$\mathrm {SSy}(M)=\mathcal {S}$
.
For each fixed
![]() $n \ge 2$
, there exist countable Scott sets
$n \ge 2$
, there exist countable Scott sets
![]() $\mathcal {S}_1$
and
$\mathcal {S}_1$
and
![]() $\mathcal {S}_2$
such that
$\mathcal {S}_2$
such that
![]() $(\omega , \mathcal {S}_1)\models \mathrm {RT}^{n}_{2}$
and
$(\omega , \mathcal {S}_1)\models \mathrm {RT}^{n}_{2}$
and
![]() $(\omega , {\mathcal {S}_2})\not \models \mathrm {RT}^{n}_{2}$
.
$(\omega , {\mathcal {S}_2})\not \models \mathrm {RT}^{n}_{2}$
.
We will sometimes want to abuse notation and use
![]() $\mathrm {Cod}(M/I)$
for the collection of n-ary relations on I coded in M, that is for
$\mathrm {Cod}(M/I)$
for the collection of n-ary relations on I coded in M, that is for
for some fixed
![]() $n> 1$
. Here
$n> 1$
. Here
![]() $\langle {i_1,\ldots ,i_n\rangle }$
is defined in terms of the usual Cantor pairing function. If I is not closed under multiplication, then such coded n-ary relations might not be elements of
$\langle {i_1,\ldots ,i_n\rangle }$
is defined in terms of the usual Cantor pairing function. If I is not closed under multiplication, then such coded n-ary relations might not be elements of
![]() $\mathrm {Cod}(M/I)$
in the strict sense, but that should not lead to any confusion.
$\mathrm {Cod}(M/I)$
in the strict sense, but that should not lead to any confusion.
We define the iterated exponential function
![]() $\exp _n(x)$
by:
$\exp _n(x)$
by:
![]() $\exp _0(x) = x$
, and
$\exp _0(x) = x$
, and
![]() $\exp _{n+1}(x) = 2^{\exp _n(x)}$
.
$\exp _{n+1}(x) = 2^{\exp _n(x)}$
.
2 Characterization in terms of cuts
In this section, we prove a basic result which underlies our subsequent analysis of Ramsey’s Theorem over
![]() $\mathrm {RCA}^*_0$
: if
$\mathrm {RCA}^*_0$
: if
![]() $\Sigma ^0_1$
induction fails but
$\Sigma ^0_1$
induction fails but
![]() $\Sigma ^0_1$
collection holds, then Ramsey’s Theorem is equivalent to its own relativization to a proper
$\Sigma ^0_1$
collection holds, then Ramsey’s Theorem is equivalent to its own relativization to a proper
![]() $\Sigma ^0_1$
-definable cut. To prove this, we make use of an important fact about coding sets in models of collection.
$\Sigma ^0_1$
-definable cut. To prove this, we make use of an important fact about coding sets in models of collection.
Lemma 2.1 [Reference Chong and Mourad5]
Let
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {B}\Sigma ^0_n$
. Then for every pair of bounded disjoint
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {B}\Sigma ^0_n$
. Then for every pair of bounded disjoint
![]() $\Sigma ^0_n$
-definable sets
$\Sigma ^0_n$
-definable sets
![]() $X,Y \subseteq M$
there exists
$X,Y \subseteq M$
there exists
![]() $A \in \mathcal {X}$
such that
$A \in \mathcal {X}$
such that
![]() $A \cap (X \cup Y) = X$
.
$A \cap (X \cup Y) = X$
.
Corollary 2.2. Let
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {B}\Sigma ^0_n$
and let
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {B}\Sigma ^0_n$
and let
![]() $I \subseteq M$
be a proper cut in M. If
$I \subseteq M$
be a proper cut in M. If
![]() $X \subseteq I$
is such that both X and
$X \subseteq I$
is such that both X and
![]() $I \setminus X$
are
$I \setminus X$
are
![]() $\Sigma ^0_n$
-definable sets, then
$\Sigma ^0_n$
-definable sets, then
![]() $X \in \mathrm {Cod}(M/I)$
.
$X \in \mathrm {Cod}(M/I)$
.
Theorem 2.3. Let
![]() $(M, \mathcal {X}) \models \mathrm {RCA}^*_0$
and let
$(M, \mathcal {X}) \models \mathrm {RCA}^*_0$
and let
![]() $I \subseteq M$
be a
$I \subseteq M$
be a
![]() $\Sigma ^0_1$
-definable proper cut in M. Then for every
$\Sigma ^0_1$
-definable proper cut in M. Then for every
![]() $n,k \in \omega $
,
$n,k \in \omega $
,
Remark. Theorem 2.3 has now been generalized from
![]() $\mathrm {RT}^n_k$
to a larger class of statements in [Reference Fiori-Carones, Kołodziejczyk and Kowalik11].
$\mathrm {RT}^n_k$
to a larger class of statements in [Reference Fiori-Carones, Kołodziejczyk and Kowalik11].
Proof Let
![]() $(M, \mathcal {X})$
be a model of
$(M, \mathcal {X})$
be a model of
![]() $\mathrm {RCA}^*_0$
and let
$\mathrm {RCA}^*_0$
and let
![]() $I \subseteq M$
be a
$I \subseteq M$
be a
![]() $\Sigma ^0_1$
-definable proper cut. Let
$\Sigma ^0_1$
-definable proper cut. Let
![]() $A \in \mathcal {X}$
be an infinite subset of M which can be enumerated in increasing order as
$A \in \mathcal {X}$
be an infinite subset of M which can be enumerated in increasing order as
![]() $\{a_i:i \in I\}$
. We may assume that
$\{a_i:i \in I\}$
. We may assume that
![]() $0 \in A$
. Fix standard
$0 \in A$
. Fix standard
![]() $n, k$
.
$n, k$
.
Suppose
![]() $(M, \mathcal {X}) \models \mathrm {RT}^n_k$
. Let
$(M, \mathcal {X}) \models \mathrm {RT}^n_k$
. Let
![]() $f \colon [I]^n \to k$
be coded by
$f \colon [I]^n \to k$
be coded by
![]() $c \in M$
. We can use f to define a colouring
$c \in M$
. We can use f to define a colouring
![]() $\check {f} \colon [A]^n \to k$
in the following way:
$\check {f} \colon [A]^n \to k$
in the following way:
In fact, it is easy to generalize the definition of
![]() $\check {f}$
to obtain a colouring of
$\check {f}$
to obtain a colouring of
![]() $[M]^n$
, which we will continue to call
$[M]^n$
, which we will continue to call
![]() $\check {f}$
:
$\check {f}$
:
 $$ \begin{align*} \check{f}(x_1,\ldots,x_n) = \begin{cases} f(i_1,\ldots,i_n), & \textrm{if } i_1 < \cdots < i_n \in I \textrm{ are such that } \\ & x_1 \in [a_{i_1},a_{i_1+1}), \ldots, x_n \in [a_{i_n},a_{i_n+1}), \\ 0, & \textrm{if there are no such } i_1,\ldots,i_n. \end{cases} \end{align*} $$
$$ \begin{align*} \check{f}(x_1,\ldots,x_n) = \begin{cases} f(i_1,\ldots,i_n), & \textrm{if } i_1 < \cdots < i_n \in I \textrm{ are such that } \\ & x_1 \in [a_{i_1},a_{i_1+1}), \ldots, x_n \in [a_{i_n},a_{i_n+1}), \\ 0, & \textrm{if there are no such } i_1,\ldots,i_n. \end{cases} \end{align*} $$
Note that
![]() $\check {f}$
is
$\check {f}$
is
![]() $\Delta _1(A,c)$
-definable, so
$\Delta _1(A,c)$
-definable, so
![]() $\check {f} \in \mathcal {X}$
. By
$\check {f} \in \mathcal {X}$
. By
![]() $\mathrm {RT}^n_k$
, there exists an infinite
$\mathrm {RT}^n_k$
, there exists an infinite
![]() $H \in \mathcal {X}$
homogeneous for
$H \in \mathcal {X}$
homogeneous for
![]() $\check {f}$
. By Corollary 2.2, the
$\check {f}$
. By Corollary 2.2, the
![]() $\Sigma _1(H)$
-definable set
$\Sigma _1(H)$
-definable set
is in
![]() $\mathrm {Cod}(M/I)$
. Clearly,
$\mathrm {Cod}(M/I)$
. Clearly,
![]() $\hat H$
is cofinal in I and homogeneous for f.
$\hat H$
is cofinal in I and homogeneous for f.
In the other direction, suppose
![]() $(I, \mathrm {Cod}(M/I)) \models \mathrm {RT}^n_k$
. Consider a colouring
$(I, \mathrm {Cod}(M/I)) \models \mathrm {RT}^n_k$
. Consider a colouring
![]() $f \colon [M]^n \to k$
. By Corollary 2.2, the colouring
$f \colon [M]^n \to k$
. By Corollary 2.2, the colouring
![]() $\hat f \colon [I]^n \to k$
given by
$\hat f \colon [I]^n \to k$
given by
is in
![]() $\mathrm {Cod}(M/I)$
. Since
$\mathrm {Cod}(M/I)$
. Since
![]() $(I, \mathrm {Cod}(M/I)) \models \mathrm {RT}^n_k$
, there is
$(I, \mathrm {Cod}(M/I)) \models \mathrm {RT}^n_k$
, there is
![]() $\mathrm {Cod}(M/I) \ni H \subseteq I$
cofinal in I and homogeneous for
$\mathrm {Cod}(M/I) \ni H \subseteq I$
cofinal in I and homogeneous for
![]() $\hat f$
. Then the set
$\hat f$
. Then the set
![]() $\check H = \{a_i: i \in H\}$
is in
$\check H = \{a_i: i \in H\}$
is in
![]() $\mathcal {X}$
and it is an infinite subset of M homogeneous for f.
$\mathcal {X}$
and it is an infinite subset of M homogeneous for f.
Remark. Note that the left-hand side of the equivalence (1) in Theorem 2.3 does not depend on the choice of the cut I, while the right-hand side does not depend on
![]() $\mathcal {X}$
, as long as I is
$\mathcal {X}$
, as long as I is
![]() $\Sigma ^0_1$
-definable in
$\Sigma ^0_1$
-definable in
![]() $(M,\mathcal {X})$
. Thus, Theorem 2.3 means that over
$(M,\mathcal {X})$
. Thus, Theorem 2.3 means that over
![]() $\mathrm {RCA}^*_0$
, once
$\mathrm {RCA}^*_0$
, once
![]() $\mathrm {I}\Sigma ^0_1$
fails, Ramsey’s Theorem becomes in some sense a first-order property. In particular, it can be satisfied in some structures of the form
$\mathrm {I}\Sigma ^0_1$
fails, Ramsey’s Theorem becomes in some sense a first-order property. In particular, it can be satisfied in some structures of the form
![]() $(M, \Delta _1$
-
$(M, \Delta _1$
-
![]() $\mathrm {Def}(M))$
(“computably true in M”). We investigate this phenomenon further in the next two sections of the paper.
$\mathrm {Def}(M))$
(“computably true in M”). We investigate this phenomenon further in the next two sections of the paper.
3 Ramsey for triples and beyond
We now use the characterization provided by Theorem 2.3 to study the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$
for
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$
for
![]() $n \ge 3$
. We begin with the easy but useful observation that, just like over
$n \ge 3$
. We begin with the easy but useful observation that, just like over
![]() $\mathrm {RCA}_0$
, the strength of Ramsey’s Theorem for n-tuples does not increase if we consider a larger but fixed number of colours.
$\mathrm {RCA}_0$
, the strength of Ramsey’s Theorem for n-tuples does not increase if we consider a larger but fixed number of colours.
Lemma 3.1. For each
![]() $n, k \ge 2$
,
$n, k \ge 2$
,
![]() $\mathrm {RCA}^*_0 \vdash (\mathrm {RT}^n_k \Leftrightarrow \mathrm {RT}^n_{k+1})$
.
$\mathrm {RCA}^*_0 \vdash (\mathrm {RT}^n_k \Leftrightarrow \mathrm {RT}^n_{k+1})$
.
Proof Assume
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$
and let
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$
and let
![]() $f \colon [\mathbb {N}]^n \to k+1$
. Consider the colouring
$f \colon [\mathbb {N}]^n \to k+1$
. Consider the colouring
![]() $g \colon [\mathbb {N}]^n \to k$
given by
$g \colon [\mathbb {N}]^n \to k$
given by
![]() $g(\bar x) = \min (f(\bar x),k-1)$
. Let A be an infinite homogeneous set for g and let
$g(\bar x) = \min (f(\bar x),k-1)$
. Let A be an infinite homogeneous set for g and let
![]() $\{a_i: i \in I\}$
be an increasing enumeration of A. (Here I may be either a proper
$\{a_i: i \in I\}$
be an increasing enumeration of A. (Here I may be either a proper
![]() $\Sigma ^0_1$
-definable cut or
$\Sigma ^0_1$
-definable cut or
![]() $\mathbb {N}$
, depending on A.)
$\mathbb {N}$
, depending on A.)
If A is j-homogeneous for g with
![]() $j < k-1$
, then A is also j-homogeneous for f, so we are done. Otherwise, A is
$j < k-1$
, then A is also j-homogeneous for f, so we are done. Otherwise, A is
![]() $(k-1)$
-homogeneous for g, which means that
$(k-1)$
-homogeneous for g, which means that
![]() $f{\upharpoonright }_{[A]^n}$
takes at most the two values
$f{\upharpoonright }_{[A]^n}$
takes at most the two values
![]() $k-1$
and k. Define a
$k-1$
and k. Define a
![]() $2$
-colouring of
$2$
-colouring of
![]() $[\mathbb {N}]^n$
by
$[\mathbb {N}]^n$
by
 $$ \begin{align*} \check{f}(x_1,\ldots,x_n) = \begin{cases} f(a_{i_1},\ldots,a_{i_n}) - k + 1, & \textrm{if } i_1 < \cdots < i_n \in I \textrm{ are such that } \\ & x_1 \in [a_{i_1},a_{i_1+1}), \ldots, x_n \in [a_{i_n},a_{i_n+1}), \\ 0, & \textrm{if there are no such } i_1,\ldots,i_n. \end{cases} \end{align*} $$
$$ \begin{align*} \check{f}(x_1,\ldots,x_n) = \begin{cases} f(a_{i_1},\ldots,a_{i_n}) - k + 1, & \textrm{if } i_1 < \cdots < i_n \in I \textrm{ are such that } \\ & x_1 \in [a_{i_1},a_{i_1+1}), \ldots, x_n \in [a_{i_n},a_{i_n+1}), \\ 0, & \textrm{if there are no such } i_1,\ldots,i_n. \end{cases} \end{align*} $$
Let H be an infinite homogeneous set for
![]() $\check {f}$
. Then the set
$\check {f}$
. Then the set
exists by
![]() $\Delta ^0_1$
-comprehension: it is clearly
$\Delta ^0_1$
-comprehension: it is clearly
![]() $\Sigma ^0_1$
-definable, and its complement is the union of
$\Sigma ^0_1$
-definable, and its complement is the union of
![]() $\mathbb {N} \setminus A$
and the
$\mathbb {N} \setminus A$
and the
![]() $\Sigma ^0_1$
-definable set
$\Sigma ^0_1$
-definable set
![]() $\{a_i: \exists a \! \in \! A\,( a> a_i \textrm { and } H \cap [a_i,a) = \emptyset )\}$
. Moreover,
$\{a_i: \exists a \! \in \! A\,( a> a_i \textrm { and } H \cap [a_i,a) = \emptyset )\}$
. Moreover,
![]() $H'$
is infinite and homogeneous for f.
$H'$
is infinite and homogeneous for f.
Definition 3.2. For
![]() $\ell \ge 1, n,k \ge 2$
, let
$\ell \ge 1, n,k \ge 2$
, let
![]() $\Delta _{\ell }$
-
$\Delta _{\ell }$
-
![]() $\mathrm {RT}^n_k$
be the first-order statement: “for every
$\mathrm {RT}^n_k$
be the first-order statement: “for every
![]() $\Delta _\ell $
-definable k-colouring of
$\Delta _\ell $
-definable k-colouring of
![]() $[\mathbb {N}]^n$
, there is a
$[\mathbb {N}]^n$
, there is a
![]() $\Delta _\ell $
-definable infinite homogeneous set.”
$\Delta _\ell $
-definable infinite homogeneous set.”
Thus, a model M satisfies
![]() $\Delta _{\ell }$
-
$\Delta _{\ell }$
-
![]() $\mathrm {RT}^n_k$
exactly if
$\mathrm {RT}^n_k$
exactly if
![]() $(M,\Delta _{\ell }$
-
$(M,\Delta _{\ell }$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^n_k$
.
$\mathrm {Def}(M)) \models \mathrm {RT}^n_k$
.
It is well known that each
![]() $\Delta _{\ell }$
-
$\Delta _{\ell }$
-
![]() $\mathrm {RT}^n_k$
is false in the standard model. However, the usual argument makes use of a nontrivial amount of induction.
$\mathrm {RT}^n_k$
is false in the standard model. However, the usual argument makes use of a nontrivial amount of induction.
Lemma 3.3. For each
![]() $n \ge 2$
:
$n \ge 2$
:
-
(a)
 $\mathrm {I} \Sigma _1$
proves that there is a
$\mathrm {I} \Sigma _1$
proves that there is a
 $\Delta _1$
-definable
$\Delta _1$
-definable
 $2$
-colouring of
$2$
-colouring of
 $[\mathbb {N}]^n$
with no
$[\mathbb {N}]^n$
with no
 $\Sigma _1$
-definable infinite homogeneous set,
$\Sigma _1$
-definable infinite homogeneous set, -
(b) for each
 $\ell \ge 1$
,
$\ell \ge 1$
,
 $\mathrm {I} \Sigma _{\ell +1}$
proves that there is a
$\mathrm {I} \Sigma _{\ell +1}$
proves that there is a
 $\Delta _{\ell }$
-definable
$\Delta _{\ell }$
-definable
 $2$
-colouring of
$2$
-colouring of
 $[\mathbb {N}]^n$
with no
$[\mathbb {N}]^n$
with no
 $\Sigma _{\ell +1}$
-definable infinite homogeneous set.
$\Sigma _{\ell +1}$
-definable infinite homogeneous set.
Proof Clearly, it is enough to prove the statement for
![]() $n = 2$
.
$n = 2$
.
The proof of (b) is just a formalization of the usual proof due to [Reference Jockusch16] in
![]() $\mathrm {I}\Sigma _{\ell +1}$
. The place where
$\mathrm {I}\Sigma _{\ell +1}$
. The place where
![]() $\Sigma _{\ell +1}$
induction is used is when we are given a hypothetical
$\Sigma _{\ell +1}$
induction is used is when we are given a hypothetical
![]() $\Delta _{\ell +1}$
-definable infinite homogeneous set with code e, and we want to reach a contradiction by looking at the first
$\Delta _{\ell +1}$
-definable infinite homogeneous set with code e, and we want to reach a contradiction by looking at the first
![]() $2e+2$
elements of this set. To do this, we need to know that the set actually has at least
$2e+2$
elements of this set. To do this, we need to know that the set actually has at least
![]() $2e+2$
elements, and this is justified by proving “for every x, the
$2e+2$
elements, and this is justified by proving “for every x, the
![]() $\Delta _{\ell +1}$
-set with code e has a finite subset with at least x elements” by induction on x.
$\Delta _{\ell +1}$
-set with code e has a finite subset with at least x elements” by induction on x.
To prove (a), one could formalize Specker’s construction [Reference Specker33] of a computable
![]() $2$
-colouring of pairs with no r.e. homogeneous set within
$2$
-colouring of pairs with no r.e. homogeneous set within
![]() $\mathrm {I} \Sigma _1$
. Instead of that, we choose to formalize a weaker variant of the argument of [Reference Jockusch16] proving (b) for
$\mathrm {I} \Sigma _1$
. Instead of that, we choose to formalize a weaker variant of the argument of [Reference Jockusch16] proving (b) for
![]() $\ell = 1$
. We define a computable function
$\ell = 1$
. We define a computable function
![]() $f \colon [\mathbb {N}]^2 \to 2$
in the following way. At stage s, we determine the values
$f \colon [\mathbb {N}]^2 \to 2$
in the following way. At stage s, we determine the values
![]() $f(n,s)$
for
$f(n,s)$
for
![]() $n < s$
. To do this, we consider all
$n < s$
. To do this, we consider all
![]() $\Sigma _{1}$
formulas with codes
$\Sigma _{1}$
formulas with codes
![]() $0,\ldots ,\lfloor (s-1)/2\rfloor $
, in that order. Given
$0,\ldots ,\lfloor (s-1)/2\rfloor $
, in that order. Given
![]() $e \le \lfloor (s-1)/2\rfloor $
, if e is the code of a
$e \le \lfloor (s-1)/2\rfloor $
, if e is the code of a
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\exists v\, \delta (x,v)$
and there are at least
$\exists v\, \delta (x,v)$
and there are at least
![]() $2e+2$
elements
$2e+2$
elements
![]() $x < s$
such that
$x < s$
such that
![]() $\exists v \! \le \! s \,\mathrm {Sat}_0(\ulcorner \delta \urcorner ,(x,v))$
holds, then choose the smallest two such elements
$\exists v \! \le \! s \,\mathrm {Sat}_0(\ulcorner \delta \urcorner ,(x,v))$
holds, then choose the smallest two such elements
![]() $x_0,x_1$
for which
$x_0,x_1$
for which
![]() $f(x_0,s), f(x_1,s)$
have not yet been defined, and let
$f(x_0,s), f(x_1,s)$
have not yet been defined, and let
![]() $f(x_i,s)=i$
. Otherwise, do nothing. Once all the formulas with codes
$f(x_i,s)=i$
. Otherwise, do nothing. Once all the formulas with codes
![]() $0,\ldots , \lfloor (s-1)/2\rfloor $
have been dealt with, complete stage s by letting
$0,\ldots , \lfloor (s-1)/2\rfloor $
have been dealt with, complete stage s by letting
![]() $f(x,s) = 0$
for all those
$f(x,s) = 0$
for all those
![]() $x<s$
for which
$x<s$
for which
![]() $f(x,s)$
was not defined earlier.
$f(x,s)$
was not defined earlier.
Now if the formula
![]() $\exists v\, \delta (x,v)$
with code e defines an infinite homogeneous set for f, we can use
$\exists v\, \delta (x,v)$
with code e defines an infinite homogeneous set for f, we can use
![]() to conclude that there are at least
to conclude that there are at least
![]() $2e + 2$
elements x such that
$2e + 2$
elements x such that
![]() $\exists v\, \delta (x,v)$
holds. Consider the
$\exists v\, \delta (x,v)$
holds. Consider the
![]() $2e + 2$
smallest such elements, say
$2e + 2$
smallest such elements, say
![]() $x_0 <\cdots < x_{2e+1}$
. By another application of
$x_0 <\cdots < x_{2e+1}$
. By another application of
![]() $\Sigma _1$
induction, there is some
$\Sigma _1$
induction, there is some
![]() $s> \max (2e, x_{2e+1})$
such that for
$s> \max (2e, x_{2e+1})$
such that for
![]() $x \le x_{2e+1}$
, if
$x \le x_{2e+1}$
, if
![]() $\exists v\, \delta (x,v)$
, then
$\exists v\, \delta (x,v)$
, then
![]() $\exists v \! \le \! s \, \delta (x,v)$
. Since there are infinitely many elements x such that
$\exists v \! \le \! s \, \delta (x,v)$
. Since there are infinitely many elements x such that
![]() $\exists v\, \delta (x,v)$
, we can also assume that
$\exists v\, \delta (x,v)$
, we can also assume that
![]() $\exists v\, \delta (s,v)$
. But the lower bounds on s imply that at stage s there will be some
$\exists v\, \delta (s,v)$
. But the lower bounds on s imply that at stage s there will be some
![]() $i < j \le 2e+1$
such that
$i < j \le 2e+1$
such that
![]() $\exists v\, \delta (x_i,v), \exists v\, \delta (x_j,v)$
, and
$\exists v\, \delta (x_i,v), \exists v\, \delta (x_j,v)$
, and
![]() $f(x_i,s) \neq f(x_j,s)$
. This is a contradiction, because all three elements
$f(x_i,s) \neq f(x_j,s)$
. This is a contradiction, because all three elements
![]() $x,x',s$
satisfy a formula that defines a homogeneous set for f.
$x,x',s$
satisfy a formula that defines a homogeneous set for f.
Lemma 3.4. Let
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
where
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
where
![]() $n \ge 3$
and assume that
$n \ge 3$
and assume that
![]() $M \models \mathrm {I}\Sigma _\ell $
. Then
$M \models \mathrm {I}\Sigma _\ell $
. Then
![]() $0^{(\ell )} \in \mathcal {X}$
. As a consequence,
$0^{(\ell )} \in \mathcal {X}$
. As a consequence,
![]() $\Delta _{\ell +1}$
-
$\Delta _{\ell +1}$
-
![]() $\mathrm {Def}(M) \subseteq \mathcal {X}$
and
$\mathrm {Def}(M) \subseteq \mathcal {X}$
and
![]() $M \models \mathrm {B} \Sigma _{\ell +1}$
.
$M \models \mathrm {B} \Sigma _{\ell +1}$
.
Proof Let
![]() $M \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2 + \mathrm {I} \Sigma _\ell $
. We will prove by induction on
$M \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2 + \mathrm {I} \Sigma _\ell $
. We will prove by induction on
![]() $j \le \ell $
that
$j \le \ell $
that
![]() $0^{(j)} \in \mathcal {X}$
. For
$0^{(j)} \in \mathcal {X}$
. For
![]() $j = \ell $
, this will immediately imply
$j = \ell $
, this will immediately imply
![]() $\Delta _{\ell +1}$
-
$\Delta _{\ell +1}$
-
![]() $\mathrm {Def}(M) \subseteq \mathcal {X}$
and
$\mathrm {Def}(M) \subseteq \mathcal {X}$
and
![]() $M \models \mathrm {B} \Sigma _{\ell +1}$
because
$M \models \mathrm {B} \Sigma _{\ell +1}$
because
![]() $(M,\mathcal {X})$
satisfies
$(M,\mathcal {X})$
satisfies
![]() $\Delta ^0_1$
comprehension and
$\Delta ^0_1$
comprehension and
![]() $\mathrm {B}\Sigma ^0_1$
.
$\mathrm {B}\Sigma ^0_1$
.
The base step of the induction holds by
![]() $\Delta ^0_1$
-comprehension in
$\Delta ^0_1$
-comprehension in
![]() $(M,\mathcal {X})$
. So, let
$(M,\mathcal {X})$
. So, let
![]() $j < \ell $
and assume that
$j < \ell $
and assume that
![]() $0^{(j)} \in \mathcal {X}$
. We have to prove that
$0^{(j)} \in \mathcal {X}$
. We have to prove that
![]() $0^{(j+1)} \in \mathcal {X}$
.
$0^{(j+1)} \in \mathcal {X}$
.
Consider the usual computable instance of
![]() $\mathrm {RT}^3_2$
whose solutions compute
$\mathrm {RT}^3_2$
whose solutions compute
![]() $0'$
and relativize it to
$0'$
and relativize it to
![]() $0^{(j)}$
:
$0^{(j)}$
:
 $$ \begin{align*} f(x,y,z) = \begin{cases} 0, & \textrm{if there is a } \Sigma_{j+1} \textrm{ sentence } \exists v\, \pi(v) \textrm{ with code at most } x \\ & \textrm{such that } \forall v \! \le \! y \,\mathrm{Sat}_j(\ulcorner\neg \pi\urcorner,v) \land \exists v \! \le \! z \,\neg\mathrm{Sat}_j(\ulcorner\neg \pi\urcorner,v), \\ 1, & \textrm{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f(x,y,z) = \begin{cases} 0, & \textrm{if there is a } \Sigma_{j+1} \textrm{ sentence } \exists v\, \pi(v) \textrm{ with code at most } x \\ & \textrm{such that } \forall v \! \le \! y \,\mathrm{Sat}_j(\ulcorner\neg \pi\urcorner,v) \land \exists v \! \le \! z \,\neg\mathrm{Sat}_j(\ulcorner\neg \pi\urcorner,v), \\ 1, & \textrm{otherwise.} \end{cases} \end{align*} $$
The colouring f is
![]() $\Delta _1(0^{(j)})$
-definable, so
$\Delta _1(0^{(j)})$
-definable, so
![]() $f \in \mathcal {X}$
. By
$f \in \mathcal {X}$
. By
![]() $\mathrm {RT}^n_2$
, there exists an infinite
$\mathrm {RT}^n_2$
, there exists an infinite
![]() $H \in \mathcal {X}$
homogeneous for f. We claim that H cannot be
$H \in \mathcal {X}$
homogeneous for f. We claim that H cannot be
![]() $0$
-homogeneous for f. To see this, note that by
$0$
-homogeneous for f. To see this, note that by
![]() $\mathrm {I} \Sigma _\ell $
we have strong
$\mathrm {I} \Sigma _\ell $
we have strong
![]() $\Sigma _{j+1}$
collection, so for any given x there is a bound w such that for any
$\Sigma _{j+1}$
collection, so for any given x there is a bound w such that for any
![]() $\Sigma _{j+1}$
sentence with code below x, if the sentence is true, then there is a witness for it below w. Thus, for any
$\Sigma _{j+1}$
sentence with code below x, if the sentence is true, then there is a witness for it below w. Thus, for any
![]() $z> y \ge w$
, we must have
$z> y \ge w$
, we must have
![]() $f(x,y,z) = 1$
, which implies that no infinite set can be
$f(x,y,z) = 1$
, which implies that no infinite set can be
![]() $0$
-homogeneous for f.
$0$
-homogeneous for f.
So, H is
![]() $1$
-homogeneous for f. We can now compute
$1$
-homogeneous for f. We can now compute
![]() $0^{(j+1)}$
with oracle access to
$0^{(j+1)}$
with oracle access to
![]() ${0^{(j)}} \oplus H$
as follows: given a
${0^{(j)}} \oplus H$
as follows: given a
![]() $\Sigma _{j+1}$
sentence
$\Sigma _{j+1}$
sentence
![]() $\exists v\, \pi (v)$
, find some
$\exists v\, \pi (v)$
, find some
![]() $x \in H$
above the code for the sentence, find
$x \in H$
above the code for the sentence, find
![]() $y \in H$
above x, and use
$y \in H$
above x, and use
![]() $0^{(j)}$
to determine whether
$0^{(j)}$
to determine whether
![]() $\exists v \! \le \! y \,\pi (v)$
holds; if it does not, then neither does
$\exists v \! \le \! y \,\pi (v)$
holds; if it does not, then neither does
![]() $\exists v\, \pi (v)$
. Both
$\exists v\, \pi (v)$
. Both
![]() $0^{(j)}$
and H are in
$0^{(j)}$
and H are in
![]() $\mathcal {X}$
, so
$\mathcal {X}$
, so
![]() $0^{(j+1)} \in \mathcal {X}$
as well.
$0^{(j+1)} \in \mathcal {X}$
as well.
We are now ready to give an axiomatization of the first-order part of
![]() $\mathrm {RCA}^*_0 +\mathrm {RT}^n_2$
for
$\mathrm {RCA}^*_0 +\mathrm {RT}^n_2$
for
![]() $n\ge 3$
. Afterwards, we will study the relationship of this theory to the usual fragments of first-order arithmetic.
$n\ge 3$
. Afterwards, we will study the relationship of this theory to the usual fragments of first-order arithmetic.
Theorem 3.5. Let
![]() $n \ge 3$
and let
$n \ge 3$
and let
![]() $\mathrm {R}^n$
be the theory:
$\mathrm {R}^n$
be the theory:
 $$ \begin{align} \left\{ (\mathrm{B} \Sigma_{\ell+1} \land \exp) \lor \bigvee_{j = 1}^{\ell} \Delta_j\textrm{-}\mathrm{RT}^n_2: \ell \in \omega \right \}. \end{align} $$
$$ \begin{align} \left\{ (\mathrm{B} \Sigma_{\ell+1} \land \exp) \lor \bigvee_{j = 1}^{\ell} \Delta_j\textrm{-}\mathrm{RT}^n_2: \ell \in \omega \right \}. \end{align} $$
Then
![]() $\mathrm {R}^n$
axiomatizes the first-order consequences of
$\mathrm {R}^n$
axiomatizes the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
Remark. By Lemma 3.3, already
![]() $\mathrm {I} \Sigma _\ell $
is inconsistent with
$\mathrm {I} \Sigma _\ell $
is inconsistent with
![]() $\Delta _\ell \textrm {-}\mathrm {RT}^n_2$
, so an equivalent axiomatization of
$\Delta _\ell \textrm {-}\mathrm {RT}^n_2$
, so an equivalent axiomatization of
![]() $\mathrm {R}^n$
would consist of
$\mathrm {R}^n$
would consist of
![]() $\mathrm {B} \Sigma _{1} + \exp $
and the sentences
$\mathrm {B} \Sigma _{1} + \exp $
and the sentences
![]() $\mathrm {B} \Sigma _\ell \Rightarrow (\mathrm {B} \Sigma _{\ell + 1} \vee \Delta _\ell \textrm {-}\mathrm {RT}^n_2)$
for all
$\mathrm {B} \Sigma _\ell \Rightarrow (\mathrm {B} \Sigma _{\ell + 1} \vee \Delta _\ell \textrm {-}\mathrm {RT}^n_2)$
for all
![]() $\ell \ge 1$
.
$\ell \ge 1$
.
Proof Fix
![]() $n \ge 3$
and let
$n \ge 3$
and let
![]() $\mathrm {R}^n$
be as in (2).
$\mathrm {R}^n$
be as in (2).
We first argue that for every
![]() $M \models \mathrm {R}^n$
there is a family of sets
$M \models \mathrm {R}^n$
there is a family of sets
![]() $\mathcal {X} \subseteq \mathcal {P}(M)$
such that
$\mathcal {X} \subseteq \mathcal {P}(M)$
such that
![]() $(M, \mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
, which will mean that
$(M, \mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
, which will mean that
![]() $\mathrm {R}^{n}\not \models \psi $
implies
$\mathrm {R}^{n}\not \models \psi $
implies
![]() $\mathrm {RCA}^{*}_{0}+\mathrm {RT}^{n}_{2}\not \models \psi $
for each arithmetical sentence
$\mathrm {RCA}^{*}_{0}+\mathrm {RT}^{n}_{2}\not \models \psi $
for each arithmetical sentence
![]() $\psi $
. So, let
$\psi $
. So, let
![]() $M \models \mathrm {R}^n$
. If
$M \models \mathrm {R}^n$
. If
![]() $M \models \mathrm {PA}$
, then
$M \models \mathrm {PA}$
, then
![]() $(M, \mathrm {Def}(M))$
is a model of
$(M, \mathrm {Def}(M))$
is a model of
![]() $\mathrm {ACA}_0$
and, a fortiori, of
$\mathrm {ACA}_0$
and, a fortiori, of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
Otherwise, let
![]() $\ell \in \omega $
be the smallest such that
$\ell \in \omega $
be the smallest such that
![]() $M \models \neg \mathrm {I} \Sigma _{\ell +1}$
. For each
$M \models \neg \mathrm {I} \Sigma _{\ell +1}$
. For each
![]() $j = 1,\ldots ,\ell $
, it follows from Lemma 3.3 that there is a
$j = 1,\ldots ,\ell $
, it follows from Lemma 3.3 that there is a
![]() $\Delta _j$
-definable
$\Delta _j$
-definable
![]() $2$
-colouring of
$2$
-colouring of
![]() $[M]^n$
with no
$[M]^n$
with no
![]() $\Delta _j$
-definable homogeneous set, so
$\Delta _j$
-definable homogeneous set, so
![]() $\mathrm {R}^n$
implies that
$\mathrm {R}^n$
implies that
![]() $\mathrm {B} \Sigma _{\ell +1} + \exp $
must hold in M. Moreover, since
$\mathrm {B} \Sigma _{\ell +1} + \exp $
must hold in M. Moreover, since
![]() $\mathrm {B} \Sigma _{\ell +2}$
fails, it must be the case that
$\mathrm {B} \Sigma _{\ell +2}$
fails, it must be the case that
![]() $M \models \Delta _{\ell +1}$
-
$M \models \Delta _{\ell +1}$
-
![]() $\mathrm {RT}^n_2$
. Thus
$\mathrm {RT}^n_2$
. Thus
![]() $(M,\Delta _{\ell +1}$
-
$(M,\Delta _{\ell +1}$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
$\mathrm {Def}(M)) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
In the other direction, we assume that
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
and prove that
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
and prove that
![]() $M \models \mathrm {R}^n$
. This is clear if
$M \models \mathrm {R}^n$
. This is clear if
![]() $M\models \mathrm {PA}$
. Otherwise, let
$M\models \mathrm {PA}$
. Otherwise, let
![]() $\ell $
be such that
$\ell $
be such that
![]() $M \models \neg \mathrm {B} \Sigma _{\ell +1}$
. Let
$M \models \neg \mathrm {B} \Sigma _{\ell +1}$
. Let
![]() $j \le \ell $
be the largest such that
$j \le \ell $
be the largest such that
![]() $M \models \mathrm {I} \Sigma _j$
. By Lemma 3.4,
$M \models \mathrm {I} \Sigma _j$
. By Lemma 3.4,
![]() $M \models \mathrm {B} \Sigma _{j+1}$
, so in particular
$M \models \mathrm {B} \Sigma _{j+1}$
, so in particular
![]() $j < \ell $
. Moreover,
$j < \ell $
. Moreover,
![]() $\Delta _{j+1}$
-
$\Delta _{j+1}$
-
![]() $\mathrm {Def}(M) \subseteq \mathcal {X}$
. We now argue that
$\mathrm {Def}(M) \subseteq \mathcal {X}$
. We now argue that
![]() $(M, \Delta _{j+1}$
-
$(M, \Delta _{j+1}$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^n_2$
, which will complete the argument.
$\mathrm {Def}(M)) \models \mathrm {RT}^n_2$
, which will complete the argument.
Let I be a
![]() $\Sigma _{j+1}$
-definable proper cut in M. The cut I is
$\Sigma _{j+1}$
-definable proper cut in M. The cut I is
![]() $\Sigma ^0_1$
-definable in
$\Sigma ^0_1$
-definable in
![]() $(M, \Delta _{j+1}$
-
$(M, \Delta _{j+1}$
-
![]() $\mathrm {Def}(M))$
and thus also in
$\mathrm {Def}(M))$
and thus also in
![]() $(M,\mathcal {X})$
. Moreover, both of these structures satisfy
$(M,\mathcal {X})$
. Moreover, both of these structures satisfy
![]() $\mathrm {RCA}^*_0$
. Therefore, Theorem 2.3 and the fact that
$\mathrm {RCA}^*_0$
. Therefore, Theorem 2.3 and the fact that
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
let us conclude that
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
let us conclude that
![]() $(M, \Delta _{j+1}$
-
$(M, \Delta _{j+1}$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^n_2$
as well.
$\mathrm {Def}(M)) \models \mathrm {RT}^n_2$
as well.
Definition 3.6. The theory
![]() $\mathrm {IB}$
is axiomatized by
$\mathrm {IB}$
is axiomatized by
![]() $\mathrm {B}\Sigma _1$
and the set of sentences
$\mathrm {B}\Sigma _1$
and the set of sentences
Kaye [Reference Kaye19] showed that
![]() $\mathrm {IB} + \exp $
implies the theory of all
$\mathrm {IB} + \exp $
implies the theory of all
![]() $\kappa $
-like models of arithmetic (for
$\kappa $
-like models of arithmetic (for
![]() $\kappa $
possibly singular). It is now known (see [Reference Haken13, Section 3.3], [Reference Belanger, Chong, Wang, Wong and Yang2, Section 6]) that
$\kappa $
possibly singular). It is now known (see [Reference Haken13, Section 3.3], [Reference Belanger, Chong, Wang, Wong and Yang2, Section 6]) that
![]() $\mathrm {IB} + \exp $
is actually strictly stronger than the theory of all
$\mathrm {IB} + \exp $
is actually strictly stronger than the theory of all
![]() $\kappa $
-like models.
$\kappa $
-like models.
Theorem 3.7. Let
![]() $n \ge 3$
. Then:
$n \ge 3$
. Then:
-
(a) The first-order consequences of
 $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
are strictly in between
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
are strictly in between
 $\mathrm {IB} + \exp $
and
$\mathrm {IB} + \exp $
and
 $\mathrm {PA}$
; as a result, they are not finitely axiomatizable.
$\mathrm {PA}$
; as a result, they are not finitely axiomatizable. -
(b) The
 $\Pi _3$
consequences of
$\Pi _3$
consequences of
 $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
coincide with
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
coincide with
 $\mathrm {B}\Sigma _1 + \exp $
; for
$\mathrm {B}\Sigma _1 + \exp $
; for
 $\ell \ge 1$
, the
$\ell \ge 1$
, the
 $\Pi _{\ell +3}$
consequences are strictly in between and
$\Pi _{\ell +3}$
consequences are strictly in between and $$\begin{align*}\mathrm{B}\Sigma_1 +{\exp} + \bigwedge_{1 \le j \le \ell}(\mathrm{I}\Sigma_j \Rightarrow \mathrm{B}\Sigma_{j+1})\end{align*}$$
$$\begin{align*}\mathrm{B}\Sigma_1 +{\exp} + \bigwedge_{1 \le j \le \ell}(\mathrm{I}\Sigma_j \Rightarrow \mathrm{B}\Sigma_{j+1})\end{align*}$$
 $\mathrm {B}\Sigma _{\ell +1}$
.
$\mathrm {B}\Sigma _{\ell +1}$
.
Proof We first prove (b). As in Theorem 3.5, we let
![]() $\mathrm {R}^n$
stand for the first-order consequences of
$\mathrm {R}^n$
stand for the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
.
It follows immediately from the definition of
![]() $\mathrm {RCA}^*_0$
and Lemma 3.4 that the
$\mathrm {RCA}^*_0$
and Lemma 3.4 that the
![]() $\Pi _{\ell +3}$
consequences of
$\Pi _{\ell +3}$
consequences of
![]() $\mathrm {R}^n$
include
$\mathrm {R}^n$
include
![]() $\mathrm {B}\Sigma _1 + {\exp }$
and
$\mathrm {B}\Sigma _1 + {\exp }$
and
![]() $\mathrm {I}\Sigma _j \Rightarrow \mathrm {B}\Sigma _{j+1}$
for each
$\mathrm {I}\Sigma _j \Rightarrow \mathrm {B}\Sigma _{j+1}$
for each
![]() $j \le \ell $
. For
$j \le \ell $
. For
![]() $\ell \ge 1$
, the inclusion is strict, because the statement
$\ell \ge 1$
, the inclusion is strict, because the statement
 $$\begin{align*}(\mathrm{B} \Sigma_{\ell+1} \land \exp) \lor \bigvee_{j = 1}^{\ell} \Delta_j\textrm{-}\mathrm{RT}^n_2\end{align*}$$
$$\begin{align*}(\mathrm{B} \Sigma_{\ell+1} \land \exp) \lor \bigvee_{j = 1}^{\ell} \Delta_j\textrm{-}\mathrm{RT}^n_2\end{align*}$$
is
![]() $\Pi _{\ell +3}$
but not provable in
$\Pi _{\ell +3}$
but not provable in
![]() $\mathrm {B}\Sigma _1 +{\exp } + \bigwedge _{1 \le j \le \ell }(\mathrm {I}\Sigma _j \Rightarrow \mathrm {B}\Sigma _{j+1})$
. To see the unprovability, consider a model
$\mathrm {B}\Sigma _1 +{\exp } + \bigwedge _{1 \le j \le \ell }(\mathrm {I}\Sigma _j \Rightarrow \mathrm {B}\Sigma _{j+1})$
. To see the unprovability, consider a model
![]() $M \models \mathrm {B}\Sigma _\ell + \exp $
such that
$M \models \mathrm {B}\Sigma _\ell + \exp $
such that
![]() $\omega $
is
$\omega $
is
![]() $\Sigma _{\ell }$
-definable in M and
$\Sigma _{\ell }$
-definable in M and
![]() $(\omega ,\mathrm {SSy}(M)) \not \models \mathrm {RT}^n_2$
. Then, clearly,
$(\omega ,\mathrm {SSy}(M)) \not \models \mathrm {RT}^n_2$
. Then, clearly,
![]() $M \models \mathrm {I}\Sigma _j \Rightarrow \mathrm {B}\Sigma _{j+1}$
for each
$M \models \mathrm {I}\Sigma _j \Rightarrow \mathrm {B}\Sigma _{j+1}$
for each
![]() $j \le \ell $
; in fact, M is a model of
$j \le \ell $
; in fact, M is a model of
![]() $\mathrm {IB}$
. However, Lemma 3.3 implies that
$\mathrm {IB}$
. However, Lemma 3.3 implies that
![]() $(M,\Delta _{j}$
-
$(M,\Delta _{j}$
-
![]() $\mathrm {Def}(M)) \not \models \mathrm {RT}^n_2$
for each
$\mathrm {Def}(M)) \not \models \mathrm {RT}^n_2$
for each
![]() $1 \le j \le \ell -1$
. On the other hand,
$1 \le j \le \ell -1$
. On the other hand,
![]() $(M,\Delta _{\ell }$
-
$(M,\Delta _{\ell }$
-
![]() $\mathrm {Def}(M))$
is a model of
$\mathrm {Def}(M))$
is a model of
![]() $\mathrm {RCA}^*_0$
in which
$\mathrm {RCA}^*_0$
in which
![]() $\omega $
is
$\omega $
is
![]() $\Sigma ^0_1$
-definable, so by Theorem 2.3 and the choice of
$\Sigma ^0_1$
-definable, so by Theorem 2.3 and the choice of
![]() $\mathrm {SSy}(M)$
it does not satisfy
$\mathrm {SSy}(M)$
it does not satisfy
![]() $\mathrm {RT}^n_2$
either.
$\mathrm {RT}^n_2$
either.
Using a model M chosen similarly but with
![]() $(\omega ,\mathrm {SSy}(M)) \models \mathrm {RT}^n_2$
, we get
$(\omega ,\mathrm {SSy}(M)) \models \mathrm {RT}^n_2$
, we get
![]() $(M,{\Delta _{\ell +1}}$
-
$(M,{\Delta _{\ell +1}}$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^n_2 + \neg \mathrm {B} \Sigma _{\ell +1}$
. Thus,
$\mathrm {Def}(M)) \models \mathrm {RT}^n_2 + \neg \mathrm {B} \Sigma _{\ell +1}$
. Thus,
![]() $\mathrm {R}^n$
does not prove
$\mathrm {R}^n$
does not prove
![]() $\mathrm {B} \Sigma _{\ell +1}$
for
$\mathrm {B} \Sigma _{\ell +1}$
for
![]() $\ell \ge 1$
.
$\ell \ge 1$
.
To see that all
![]() $\Pi _{\ell + 3}$
consequences of
$\Pi _{\ell + 3}$
consequences of
![]() $\mathrm {R}^n$
follow from
$\mathrm {R}^n$
follow from
![]() $\mathrm {B}\Sigma _{\ell +1}$
for
$\mathrm {B}\Sigma _{\ell +1}$
for
![]() $\ell \ge 1$
let the
$\ell \ge 1$
let the
![]() $\Sigma _{\ell + 3}$
formula
$\Sigma _{\ell + 3}$
formula
![]() $\psi := \exists x\, \forall y\, \exists z\, \pi (x,y,z)$
be consistent with
$\psi := \exists x\, \forall y\, \exists z\, \pi (x,y,z)$
be consistent with
![]() $\mathrm {B}\Sigma _{\ell +1}$
, let
$\mathrm {B}\Sigma _{\ell +1}$
, let
![]() $K \models \mathrm {B}\Sigma _{\ell +1} \land \psi $
be such that
$K \models \mathrm {B}\Sigma _{\ell +1} \land \psi $
be such that
![]() $(\omega ,\mathrm {SSy}(K)) \models \mathrm {RT}^n_2$
, and let
$(\omega ,\mathrm {SSy}(K)) \models \mathrm {RT}^n_2$
, and let
![]() $a \in K$
be a witness for the initial existential quantifier in
$a \in K$
be a witness for the initial existential quantifier in
![]() $\psi $
. By
$\psi $
. By
![]() $\mathrm {B}\Sigma _{\ell +1}$
, the function
$\mathrm {B}\Sigma _{\ell +1}$
, the function
 $$ \begin{align*} f(y) & =\textrm{least } w> y \textrm{ such that } \forall y' \! \le \! y \,\exists z \! \le \! w \,\pi(a,y',z) \\ & ~~~~\textrm{and "true }\Sigma_\ell \textrm{ sentences with codes } {\le y} \textrm{ are witnessed } {\le w}\textrm{"} \end{align*} $$
$$ \begin{align*} f(y) & =\textrm{least } w> y \textrm{ such that } \forall y' \! \le \! y \,\exists z \! \le \! w \,\pi(a,y',z) \\ & ~~~~\textrm{and "true }\Sigma_\ell \textrm{ sentences with codes } {\le y} \textrm{ are witnessed } {\le w}\textrm{"} \end{align*} $$
is total and
![]() $\Delta _{\ell +1}$
-definable in K. Let M be the cut
$\Delta _{\ell +1}$
-definable in K. Let M be the cut
![]() $\sup _K(\{f^{m}(a): m \in \omega \})$
. Then
$\sup _K(\{f^{m}(a): m \in \omega \})$
. Then
![]() $M \models \mathrm {B}\Sigma _{\ell +1}\land \psi $
and
$M \models \mathrm {B}\Sigma _{\ell +1}\land \psi $
and
![]() $\omega $
is
$\omega $
is
![]() $\Sigma _{\ell +1}$
-definable in M. Since
$\Sigma _{\ell +1}$
-definable in M. Since
![]() $(\omega ,\mathrm {SSy}(M)) \models \mathrm {RT}^n_2$
, we get
$(\omega ,\mathrm {SSy}(M)) \models \mathrm {RT}^n_2$
, we get
![]() $(M,\Delta _{\ell }$
-
$(M,\Delta _{\ell }$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^n_2$
by Theorem 2.3, so
$\mathrm {Def}(M)) \models \mathrm {RT}^n_2$
by Theorem 2.3, so
![]() $M \models \mathrm {R}^n \land \psi $
.
$M \models \mathrm {R}^n \land \psi $
.
The proof that the
![]() $\Pi _3$
consequences of
$\Pi _3$
consequences of
![]() $\mathrm {R}^n$
follow from
$\mathrm {R}^n$
follow from
![]() $\mathrm {B}\Sigma _{1} + \exp $
is very similar, except that the function f is now defined by
$\mathrm {B}\Sigma _{1} + \exp $
is very similar, except that the function f is now defined by
where
![]() $\pi $
is now a
$\pi $
is now a
![]() $\Delta _0$
formula. The difference is due to the fact that for
$\Delta _0$
formula. The difference is due to the fact that for
![]() $\ell = 0$
we no longer have to care about elementarity between the cut M and the model K to ensure that
$\ell = 0$
we no longer have to care about elementarity between the cut M and the model K to ensure that
![]() $M \models \mathrm {B}\Sigma _{\ell +1}\land \psi $
, but we need to guarantee that
$M \models \mathrm {B}\Sigma _{\ell +1}\land \psi $
, but we need to guarantee that
![]() $M \models \exp $
.
$M \models \exp $
.
We have thus proved (b). Regarding (a), note that the containments
follow directly from the statement of (b), and in the proof of (b) we constructed a model of
![]() $\mathrm {IB} + \exp $
not satisfying
$\mathrm {IB} + \exp $
not satisfying
![]() $\mathrm {R}^n$
. Finally, observe that
$\mathrm {R}^n$
. Finally, observe that
![]() $\mathrm {IB}$
is not contained in any
$\mathrm {IB}$
is not contained in any
![]() $\mathrm {I}\Sigma _\ell $
, so any subtheory of
$\mathrm {I}\Sigma _\ell $
, so any subtheory of
![]() $\mathrm {PA}$
extending
$\mathrm {PA}$
extending
![]() $\mathrm {IB}$
cannot be finitely axiomatizable.
$\mathrm {IB}$
cannot be finitely axiomatizable.
Note that the proof of Theorem 3.7 immediately gives the following statement, which says essentially that Lemma 3.3 is optimal with respect to the amount of induction used to prove the existence of colourings without simple homogeneous sets.
Corollary 3.8. For each
![]() $\ell \ge 1, n\ge 2$
, the theory
$\ell \ge 1, n\ge 2$
, the theory
![]() $\mathrm {B}\Sigma _{\ell } + {\exp } + \Delta _{\ell }$
-
$\mathrm {B}\Sigma _{\ell } + {\exp } + \Delta _{\ell }$
-
![]() $\mathrm {RT}^n_2$
is consistent.
$\mathrm {RT}^n_2$
is consistent.
Remark. As mentioned in Section 1, results such as Theorem 3.7 can be converted from purely arithmetical to
![]() $\Pi ^{1}_{1}$
form by relativizing to second-order parameters. In Theorem 3.7
(a), the appropriate relativization of the scheme
$\Pi ^{1}_{1}$
form by relativizing to second-order parameters. In Theorem 3.7
(a), the appropriate relativization of the scheme
![]() $\mathrm {IB}$
takes the form
$\mathrm {IB}$
takes the form
![]() $\forall X\,(\mathrm {I} \Sigma _k(X) \Rightarrow \mathrm {B} \Sigma _{k+1}(X))$
for each k. In Section 4, we will also consider a weaker relativization of
$\forall X\,(\mathrm {I} \Sigma _k(X) \Rightarrow \mathrm {B} \Sigma _{k+1}(X))$
for each k. In Section 4, we will also consider a weaker relativization of
![]() $\mathrm {IB}$
: see the remark after Corollary 4.4.
$\mathrm {IB}$
: see the remark after Corollary 4.4.
Question 1. Does
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^3_2$
imply
$\mathrm {RCA}^*_0 + \mathrm {RT}^3_2$
imply
![]() $\mathrm {RT}^4_2$
? More generally, does
$\mathrm {RT}^4_2$
? More generally, does
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
imply
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
imply
![]() $\mathrm {RT}^{n+1}_2$
for some/all
$\mathrm {RT}^{n+1}_2$
for some/all
![]() $n \ge 3$
?
$n \ge 3$
?
4 Ramsey for pairs
We turn to the case of Ramsey’s Theorem for pairs. Here, we are not able to give a complete axiomatization analogous to that of Theorem 3.5. Loosely speaking, our understanding of the strength of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
strongly depends on the amount of induction satisfied by the underlying first-order model.
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
strongly depends on the amount of induction satisfied by the underlying first-order model.
Theorem 4.1. Let
![]() $\mathrm {R}^2$
stand for the first-order consequences of
$\mathrm {R}^2$
stand for the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
. Then:
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
. Then:
-
(a)
 $\mathrm {R}^2 \land \neg \mathrm {I} \Sigma _1$
is axiomatized by
$\mathrm {R}^2 \land \neg \mathrm {I} \Sigma _1$
is axiomatized by
 $\mathrm {B}\Sigma _1+ {\exp }+ \Delta _1$
-
$\mathrm {B}\Sigma _1+ {\exp }+ \Delta _1$
-
 $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
. -
(b)
 $\mathrm {I} \Sigma _2$
implies
$\mathrm {I} \Sigma _2$
implies
 $\mathrm {R}^2$
.
$\mathrm {R}^2$
. -
(c) Over
 $\mathrm {B}\Sigma _2$
,
$\mathrm {B}\Sigma _2$
,
 $\mathrm {R}^2$
is implied by, and consistent with, both the first-order consequences of
$\mathrm {R}^2$
is implied by, and consistent with, both the first-order consequences of
 $\mathrm {RCA}_0 +\mathrm {RT}^2_2$
and the statement
$\mathrm {RCA}_0 +\mathrm {RT}^2_2$
and the statement
 $\Delta _2$
-
$\Delta _2$
-
 $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
. -
(d)
 $\mathrm {R}^2$
implies every first-order sentence
$\mathrm {R}^2$
implies every first-order sentence
 $\psi $
such that both
$\psi $
such that both
 $\mathrm {B} \Sigma _2 \vdash \psi $
and
$\mathrm {B} \Sigma _2 \vdash \psi $
and
 $\mathrm {RCA}^*_0 + \neg \mathrm {I}\Sigma ^0_1 \vdash \psi $
.
$\mathrm {RCA}^*_0 + \neg \mathrm {I}\Sigma ^0_1 \vdash \psi $
.
Proof We first prove (a). Clearly, if
![]() $M\models \mathrm {B}\Sigma _1 + \exp $
and
$M\models \mathrm {B}\Sigma _1 + \exp $
and
![]() $(M,\Delta _{1}$
-
$(M,\Delta _{1}$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^2_2$
, then M satisfies
$\mathrm {Def}(M)) \models \mathrm {RT}^2_2$
, then M satisfies
![]() $\mathrm {R}^2$
(as well as
$\mathrm {R}^2$
(as well as
![]() $\neg \mathrm {I}\Sigma _1$
, by Lemma 3.3). On the other hand, let
$\neg \mathrm {I}\Sigma _1$
, by Lemma 3.3). On the other hand, let
![]() $(M,\mathcal {X}) \models {\mathrm {RCA}^*_0} + {\mathrm {RT}^2_2} + {\neg \mathrm {I}\Sigma _1}$
. Obviously, M satisfies
$(M,\mathcal {X}) \models {\mathrm {RCA}^*_0} + {\mathrm {RT}^2_2} + {\neg \mathrm {I}\Sigma _1}$
. Obviously, M satisfies
![]() $\mathrm {B} \Sigma _1 + \exp $
. Let I be a proper
$\mathrm {B} \Sigma _1 + \exp $
. Let I be a proper
![]() $\Sigma _1$
-definable cut in M. Applying Theorem 2.3 two times, we get first
$\Sigma _1$
-definable cut in M. Applying Theorem 2.3 two times, we get first
![]() $(I,\mathrm {Cod}(M/I)) \models \mathrm {RT}^2_2$
and then
$(I,\mathrm {Cod}(M/I)) \models \mathrm {RT}^2_2$
and then
![]() $(M,\Delta _{1}$
-
$(M,\Delta _{1}$
-
![]() $\mathrm {Def}(M)) \models \mathrm {RT}^2_2$
.
$\mathrm {Def}(M)) \models \mathrm {RT}^2_2$
.
Statement (b) follows immediately from the result of [Reference Cholak, Jockusch and Slaman4] that
![]() $\mathrm {RCA}_0 + \mathrm {I}\Sigma ^0_2 + \mathrm {RT}^2_2$
is conservative over
$\mathrm {RCA}_0 + \mathrm {I}\Sigma ^0_2 + \mathrm {RT}^2_2$
is conservative over
![]() $\mathrm {I}\Sigma _2$
.
$\mathrm {I}\Sigma _2$
.
We turn to (c). It is clear that
![]() $\mathrm {R}^2$
is implied by the first-order consequences of
$\mathrm {R}^2$
is implied by the first-order consequences of
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
. Meanwhile,
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
. Meanwhile,
![]() $\mathrm {R}^2$
is also satisfied by any model
$\mathrm {R}^2$
is also satisfied by any model
![]() $M \models \mathrm {B}\Sigma _2 + \Delta _{2}$
-
$M \models \mathrm {B}\Sigma _2 + \Delta _{2}$
-
![]() $\mathrm {RT}^2_2$
since
$\mathrm {RT}^2_2$
since
![]() $(M, \Delta _2$
-
$(M, \Delta _2$
-
![]() $\mathrm {Def}(M))\models \mathrm {RCA}^*_0+\mathrm {RT}^{2}_{2}$
. The consistency of
$\mathrm {Def}(M))\models \mathrm {RCA}^*_0+\mathrm {RT}^{2}_{2}$
. The consistency of
![]() $\mathrm {B}\Sigma _2 + \Delta _{2}$
-
$\mathrm {B}\Sigma _2 + \Delta _{2}$
-
![]() $\mathrm {RT}^2_2$
is Corollary 3.8 for
$\mathrm {RT}^2_2$
is Corollary 3.8 for
![]() $\ell = n =2$
.
$\ell = n =2$
.
Finally, to see that (d) holds, let
![]() $\psi $
be provable both in
$\psi $
be provable both in
![]() $\mathrm {B} \Sigma _2$
and in
$\mathrm {B} \Sigma _2$
and in
![]() $\mathrm {RCA}^*_0 + \neg \mathrm {I}\Sigma ^0_1$
. We check that
$\mathrm {RCA}^*_0 + \neg \mathrm {I}\Sigma ^0_1$
. We check that
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2\vdash \psi $
. Let
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2\vdash \psi $
. Let
![]() $(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^2_2 $
. If
$(M,\mathcal {X}) \models \mathrm {RCA}^*_0 + \mathrm {RT}^2_2 $
. If
![]() $(M,\mathcal {X}) \models \mathrm {RCA}_0$
, then
$(M,\mathcal {X}) \models \mathrm {RCA}_0$
, then
![]() $M \models \mathrm {B}\Sigma _2$
, so
$M \models \mathrm {B}\Sigma _2$
, so
![]() $M \models \psi $
. Otherwise,
$M \models \psi $
. Otherwise,
![]() $M \models \mathrm {RCA}^*_0 + \neg \mathrm {I}\Sigma ^0_1$
, so
$M \models \mathrm {RCA}^*_0 + \neg \mathrm {I}\Sigma ^0_1$
, so
![]() $M \models \psi $
as well.
$M \models \psi $
as well.
Parts (a) and (b) of Theorem 4.1 give a complete axiomatization of the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
over, respectively,
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
over, respectively,
![]() $\neg \mathrm {I}\Sigma _1$
and
$\neg \mathrm {I}\Sigma _1$
and
![]() $\mathrm {I} \Sigma _2$
. However, the situation in the region between
$\mathrm {I} \Sigma _2$
. However, the situation in the region between
![]() $\mathrm {I} \Sigma _1$
and
$\mathrm {I} \Sigma _1$
and
![]() $\mathrm {I} \Sigma _2$
is much less clear.
$\mathrm {I} \Sigma _2$
is much less clear.
As mentioned in the introduction, it is open whether
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
is arithmetically conservative over
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
is arithmetically conservative over
![]() $\mathrm {B}\Sigma _2$
. Therefore, it is consistent with what we know that already
$\mathrm {B}\Sigma _2$
. Therefore, it is consistent with what we know that already
![]() $\mathrm {B}\Sigma _2$
implies the first-order consequences of
$\mathrm {B}\Sigma _2$
implies the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
.
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
.
On the other hand, we will now use Theorem 4.1
(d) to show that there are some first-order sentences provable in
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
but not in
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
but not in
![]() $\mathrm {I} \Sigma _1$
. It will be clear from our argument that this is not a feature of
$\mathrm {I} \Sigma _1$
. It will be clear from our argument that this is not a feature of
![]() $\mathrm {RT}^2_2$
specifically, but rather of all principles that imply
$\mathrm {RT}^2_2$
specifically, but rather of all principles that imply
![]() $\mathrm {B}\Sigma ^0_2$
(or even somewhat weaker statements) over
$\mathrm {B}\Sigma ^0_2$
(or even somewhat weaker statements) over
![]() $\mathrm {RCA}_0$
.
$\mathrm {RCA}_0$
.
Definition 4.2. For each
![]() $\ell \ge 1$
, the
$\ell \ge 1$
, the
![]() $\Sigma _\ell $
cardinality scheme,
$\Sigma _\ell $
cardinality scheme,
![]() $\mathrm {C}\Sigma _\ell $
, asserts that no
$\mathrm {C}\Sigma _\ell $
, asserts that no
![]() $\Sigma _\ell $
formula defines a total injection with bounded range.
$\Sigma _\ell $
formula defines a total injection with bounded range.
The
![]() $\Sigma _\ell $
generalized pigeonhole principle,
$\Sigma _\ell $
generalized pigeonhole principle,
![]() $\mathrm {GPHP}(\Sigma _\ell )$
, asserts that for every
$\mathrm {GPHP}(\Sigma _\ell )$
, asserts that for every
![]() $\Sigma _\ell $
formula
$\Sigma _\ell $
formula
![]() $\varphi (x,y,z)$
and every number a, there exists a number b such that there is no c for which
$\varphi (x,y,z)$
and every number a, there exists a number b such that there is no c for which
![]() $\varphi (\cdot ,\cdot ,c)$
defines an injective multifunction from b into a:
$\varphi (\cdot ,\cdot ,c)$
defines an injective multifunction from b into a:
The principle
![]() $\mathrm {C}\Sigma _\ell $
was defined in [Reference Seetapun and Slaman29]. It is known that
$\mathrm {C}\Sigma _\ell $
was defined in [Reference Seetapun and Slaman29]. It is known that
![]() $\mathrm {I}\Sigma _\ell $
does not imply
$\mathrm {I}\Sigma _\ell $
does not imply
![]() $\mathrm {C}\Sigma _{\ell +1}$
[Reference Groszek and Slaman12, Proposition 3.1]. The principle
$\mathrm {C}\Sigma _{\ell +1}$
[Reference Groszek and Slaman12, Proposition 3.1]. The principle
![]() $\mathrm {GPHP}(\Sigma _\ell )$
was defined in [Reference Kaye19], where it was also observed that the theory of all
$\mathrm {GPHP}(\Sigma _\ell )$
was defined in [Reference Kaye19], where it was also observed that the theory of all
![]() $\kappa $
-like models of
$\kappa $
-like models of
![]() $\mathrm {I}\Delta _0$
implies
$\mathrm {I}\Delta _0$
implies
![]() $\mathrm {GPHP}(\Sigma _\ell )$
for all
$\mathrm {GPHP}(\Sigma _\ell )$
for all
![]() $\ell $
.
$\ell $
.
Clearly,
![]() $\mathrm {GPHP}(\Sigma _\ell )$
implies
$\mathrm {GPHP}(\Sigma _\ell )$
implies
![]() $\mathrm {C}\Sigma _\ell $
for each
$\mathrm {C}\Sigma _\ell $
for each
![]() $\ell \ge 1$
. In turn,
$\ell \ge 1$
. In turn,
![]() $\mathrm {GPHP}(\Sigma _\ell )$
is implied by
$\mathrm {GPHP}(\Sigma _\ell )$
is implied by
![]() $\mathrm {B}\Sigma _\ell $
for
$\mathrm {B}\Sigma _\ell $
for
![]() $\ell \ge 2$
, and
$\ell \ge 2$
, and
![]() $\mathrm {GPHP}(\Sigma _1)$
is implied by
$\mathrm {GPHP}(\Sigma _1)$
is implied by
![]() $\mathrm {B}\Sigma _1 + \exp $
, because
$\mathrm {B}\Sigma _1 + \exp $
, because
![]() $\mathrm {B}\Sigma _\ell $
is for each
$\mathrm {B}\Sigma _\ell $
is for each
![]() $\ell \ge 1$
equivalent over
$\ell \ge 1$
equivalent over
![]() $\mathrm {I}\Delta _0 +\exp $
to the usual pigeonhole principle for
$\mathrm {I}\Delta _0 +\exp $
to the usual pigeonhole principle for
![]() $\Sigma _\ell $
maps [Reference Dimitracopoulos and Paris9]. It follows from [Reference Belanger, Chong, Wang, Wong and Yang2] that the implications from
$\Sigma _\ell $
maps [Reference Dimitracopoulos and Paris9]. It follows from [Reference Belanger, Chong, Wang, Wong and Yang2] that the implications from
![]() $\mathrm {B}\Sigma _\ell $
to
$\mathrm {B}\Sigma _\ell $
to
![]() $\mathrm {GPHP}(\Sigma _\ell )$
are strict.
$\mathrm {GPHP}(\Sigma _\ell )$
are strict.
![]() $\mathrm {C}\Sigma _2$
is known to be a consequence of some theories studied in reverse mathematics that do not imply
$\mathrm {C}\Sigma _2$
is known to be a consequence of some theories studied in reverse mathematics that do not imply
![]() $\mathrm {B}\Sigma _2$
, such as
$\mathrm {B}\Sigma _2$
, such as
![]() $\mathrm {RCA}_0$
plus the Rainbow Ramsey Theorem for pairs [Reference Conidis and Slaman8] and
$\mathrm {RCA}_0$
plus the Rainbow Ramsey Theorem for pairs [Reference Conidis and Slaman8] and
![]() $\mathrm {RCA}_0$
plus the existence of 2-random reals [Reference Haken13].
$\mathrm {RCA}_0$
plus the existence of 2-random reals [Reference Haken13].
In the theorem below, we explicitly indicate second-order variables to emphasize the role played by set parameters in the second part of the statement. Recall that
![]() $\mathrm {I}\Sigma ^{0}_{k}$
(resp.
$\mathrm {I}\Sigma ^{0}_{k}$
(resp.
![]() $\mathrm {B}\Sigma ^{0}_{k}$
) means
$\mathrm {B}\Sigma ^{0}_{k}$
) means
![]() $\forall X\,\mathrm {I}\Sigma _{k}(X)$
(resp.
$\forall X\,\mathrm {I}\Sigma _{k}(X)$
(resp.
![]() $\forall X\,\mathrm {B}\Sigma _{k}(X)$
).
$\forall X\,\mathrm {B}\Sigma _{k}(X)$
).
Theorem 4.3. For each
![]() $k,\ell \ge 1$
, the following statements are provable in
$k,\ell \ge 1$
, the following statements are provable in
![]() $\mathrm {RCA}^*_0$
:
$\mathrm {RCA}^*_0$
:
-
(a)
 $\forall X\,(\mathrm {B}\Sigma _\ell (X)\Rightarrow \mathrm {GPHP}(\Sigma _\ell (X)))$
,
$\forall X\,(\mathrm {B}\Sigma _\ell (X)\Rightarrow \mathrm {GPHP}(\Sigma _\ell (X)))$
, -
(b)
 $(\mathrm {B}\Sigma ^{0}_{k} \wedge \neg \mathrm {I}\Sigma ^0_{k})\Rightarrow \forall X\,\mathrm {GPHP}(\Sigma _\ell (X))$
.
$(\mathrm {B}\Sigma ^{0}_{k} \wedge \neg \mathrm {I}\Sigma ^0_{k})\Rightarrow \forall X\,\mathrm {GPHP}(\Sigma _\ell (X))$
.
Theorem 4.3
(b) can be obtained by relativizing Kaye’s proof of the result that any model of
![]() $\mathrm {B}\Sigma _1 + {\exp } + {\neg \mathrm {I}\Sigma _1}$
is elementarily equivalent to an
$\mathrm {B}\Sigma _1 + {\exp } + {\neg \mathrm {I}\Sigma _1}$
is elementarily equivalent to an
![]() $\aleph _\omega $
-like structure [Reference Kaye19, Theorem 2.4]. A model of
$\aleph _\omega $
-like structure [Reference Kaye19, Theorem 2.4]. A model of
![]() $\neg \mathrm {I}\Sigma _1(A) + \neg \mathrm {GPHP}(\Sigma _\ell (B)) + \mathrm {B}\Sigma _1(A\oplus B) + \exp $
would also be elementarily equivalent to an
$\neg \mathrm {I}\Sigma _1(A) + \neg \mathrm {GPHP}(\Sigma _\ell (B)) + \mathrm {B}\Sigma _1(A\oplus B) + \exp $
would also be elementarily equivalent to an
![]() $\aleph _\omega $
-like model, but clearly such a structure can never violate the scheme
$\aleph _\omega $
-like model, but clearly such a structure can never violate the scheme
![]() $\mathrm {GPHP}(\Gamma )$
for any class of formulas
$\mathrm {GPHP}(\Gamma )$
for any class of formulas
![]() $\Gamma $
.
$\Gamma $
.
The proof of Theorem 4.3 we give below is considerably simpler than that of [Reference Kaye19, Theorem 2.4]. On the other hand, both make use of an automorphism argument. It would be interesting to come up with a direct proof of
![]() $\mathrm {GPHP}(\Sigma _\ell )$
, with no model-theoretic detours, in for instance
$\mathrm {GPHP}(\Sigma _\ell )$
, with no model-theoretic detours, in for instance
![]() ${\mathrm {B}\Sigma _1} + {\exp } + {\neg \mathrm {I}\Sigma _1}$
.
${\mathrm {B}\Sigma _1} + {\exp } + {\neg \mathrm {I}\Sigma _1}$
.
Proof It has already been mentioned that
![]() $\mathrm {B}\Sigma _\ell + \exp $
implies
$\mathrm {B}\Sigma _\ell + \exp $
implies
![]() $\mathrm {GPHP}(\Sigma _\ell )$
. The argument for this relativizes with no issues, thus proving part (a).
$\mathrm {GPHP}(\Sigma _\ell )$
. The argument for this relativizes with no issues, thus proving part (a).
It remains to prove that
![]() $\mathrm {RCA}^*_0 +\mathrm {B}\Sigma ^{0}_{k} + \neg \mathrm {I}\Sigma ^0_{k}$
implies
$\mathrm {RCA}^*_0 +\mathrm {B}\Sigma ^{0}_{k} + \neg \mathrm {I}\Sigma ^0_{k}$
implies
![]() $\mathrm {GPHP}(\Sigma ^0_\ell )$
for any
$\mathrm {GPHP}(\Sigma ^0_\ell )$
for any
![]() $\ell $
. To simplify notation, we restrict ourselves to the case where
$\ell $
. To simplify notation, we restrict ourselves to the case where
![]() $k=1$
and to
$k=1$
and to
![]() $\mathrm {GPHP}$
for lightface
$\mathrm {GPHP}$
for lightface
![]() $\Sigma _\ell $
formulas. The general case for
$\Sigma _\ell $
formulas. The general case for
![]() $k \ge 1$
and a
$k \ge 1$
and a
![]() $\Sigma _\ell (B)$
formula reduces to this one by considering the model of
$\Sigma _\ell (B)$
formula reduces to this one by considering the model of
![]() $\mathrm {RCA}^*_0$
given by the
$\mathrm {RCA}^*_0$
given by the
![]() $\Delta _k(A\oplus B)$
-definable sets, where A is a parameter witnessing the failure of
$\Delta _k(A\oplus B)$
-definable sets, where A is a parameter witnessing the failure of
![]() $\mathrm {I}\Sigma ^0_k$
.
$\mathrm {I}\Sigma ^0_k$
.
Let
![]() $(M,A)$
be a countable model of
$(M,A)$
be a countable model of
![]() $\mathrm {B}\Sigma _1(A) + {\exp } + \neg \mathrm {I}\Sigma _1(A)$
. We may assume that A itself has an increasing enumeration
$\mathrm {B}\Sigma _1(A) + {\exp } + \neg \mathrm {I}\Sigma _1(A)$
. We may assume that A itself has an increasing enumeration
![]() $A = \{a_i: i \in I\}$
for a proper cut
$A = \{a_i: i \in I\}$
for a proper cut
![]() ${I \subseteq M}$
. By a routine compactness argument, we may also assume that for every
${I \subseteq M}$
. By a routine compactness argument, we may also assume that for every
![]() $a \in M$
there is some
$a \in M$
there is some
![]() $b \in M$
such that
$b \in M$
such that
![]() $b> \exp _m(a)$
for each
$b> \exp _m(a)$
for each
![]() $m \in \omega $
. To prove that
$m \in \omega $
. To prove that
![]() $M \models \mathrm {GPHP}(\Sigma _\ell )$
, we will use a technique based on the fact that models of
$M \models \mathrm {GPHP}(\Sigma _\ell )$
, we will use a technique based on the fact that models of
![]() $\mathrm {B}\Sigma ^0_1 + {\exp } + {\neg \mathrm {I}\Sigma ^0_1}$
have many automorphisms [Reference Kaye17, Reference Kossak23, Reference Kossak24].
$\mathrm {B}\Sigma ^0_1 + {\exp } + {\neg \mathrm {I}\Sigma ^0_1}$
have many automorphisms [Reference Kaye17, Reference Kossak23, Reference Kossak24].
By a standard argument (see, e.g., [Reference Enayat and Wong10, Theorem 4.6]), the model M can be end-extended to a model
![]() $K \models \mathrm {I} \Delta _0$
such that
$K \models \mathrm {I} \Delta _0$
such that
![]() $A \in \mathrm {Cod}(K/M)$
. Since elements coding A are downwards cofinal in
$A \in \mathrm {Cod}(K/M)$
. Since elements coding A are downwards cofinal in
![]() $K \setminus M$
, there is an element
$K \setminus M$
, there is an element
![]() $d \in K$
coding A and small enough that
$d \in K$
coding A and small enough that
![]() $\exp _2(d)$
exists in K. By [Reference Lessan26], there is a
$\exp _2(d)$
exists in K. By [Reference Lessan26], there is a
![]() $\Delta _0$
formula with parameter
$\Delta _0$
formula with parameter
![]() $\exp _2(d)$
that defines satisfaction for
$\exp _2(d)$
that defines satisfaction for
![]() $\Delta _0$
formulas on arguments below d. As a consequence, the structure
$\Delta _0$
formulas on arguments below d. As a consequence, the structure
![]() $[0,d]$
(with addition and multiplication as ternary relations) is recursively saturated.
$[0,d]$
(with addition and multiplication as ternary relations) is recursively saturated.
Now let
![]() $a \in M\setminus I$
and let
$a \in M\setminus I$
and let
![]() $b\in M$
be such that
$b\in M$
be such that
![]() $b> \exp _m(a)$
for each
$b> \exp _m(a)$
for each
![]() $m \in \omega $
. Let
$m \in \omega $
. Let
![]() $c \in M$
be arbitrary. The recursive saturation of
$c \in M$
be arbitrary. The recursive saturation of
![]() $[0,d]$
lets us use an argument dating back to [Reference Kotlarski25] (see the proof of Lemma 3.4 in [Reference Kaye17] for a detailed argument and [Reference Kossak24] for a brief discussion) to derive the existence of an automorphism
$[0,d]$
lets us use an argument dating back to [Reference Kotlarski25] (see the proof of Lemma 3.4 in [Reference Kaye17] for a detailed argument and [Reference Kossak24] for a brief discussion) to derive the existence of an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $[0,d]$
such that
$[0,d]$
such that
![]() $\alpha $
fixes
$\alpha $
fixes
![]() $c,d$
and fixes
$c,d$
and fixes
![]() $[0,a]$
pointwise, but there is some
$[0,a]$
pointwise, but there is some
![]() $x < b$
with
$x < b$
with
![]() $x \neq \alpha (x)=:y$
. For each
$x \neq \alpha (x)=:y$
. For each
![]() $i \in I$
, since
$i \in I$
, since
![]() $\alpha (i) = i$
,
$\alpha (i) = i$
,
![]() $\alpha (d) = d$
, and d codes A, we know that
$\alpha (d) = d$
, and d codes A, we know that
![]() $\alpha (a_i) = a_i$
. Therefore,
$\alpha (a_i) = a_i$
. Therefore,
![]() $\alpha [M] = M$
, so
$\alpha [M] = M$
, so
![]() $\alpha {\upharpoonright }_M$
is actually an automorphism of M. We now argue that no injective multifunction from b to a is definable in M with c as parameter. Otherwise, if f were such a multifunction, there would be some
$\alpha {\upharpoonright }_M$
is actually an automorphism of M. We now argue that no injective multifunction from b to a is definable in M with c as parameter. Otherwise, if f were such a multifunction, there would be some
![]() $z < a$
such that
$z < a$
such that
![]() $z \in f(x)$
, and therefore (since
$z \in f(x)$
, and therefore (since
![]() $\alpha $
fixes both z and c) also
$\alpha $
fixes both z and c) also
![]() $z = \alpha (z) \in f(\alpha (x)) = f(y)$
. By the injectivity of f, this would imply
$z = \alpha (z) \in f(\alpha (x)) = f(y)$
. By the injectivity of f, this would imply
![]() $x = y$
, a contradiction. Since
$x = y$
, a contradiction. Since
![]() $c \in M$
was arbitrary, this proves that there can be no injective multifunction from b to a definable in M, so
$c \in M$
was arbitrary, this proves that there can be no injective multifunction from b to a definable in M, so
![]() $M \models \mathrm {GPHP}(\Sigma _\ell )$
for each
$M \models \mathrm {GPHP}(\Sigma _\ell )$
for each
![]() $\ell $
.
$\ell $
.
Corollary 4.4.
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
proves both
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
proves both
![]() $\mathrm {C}\Sigma _2$
and
$\mathrm {C}\Sigma _2$
and
![]() $\mathrm {GPHP}(\Sigma _2)$
.
$\mathrm {GPHP}(\Sigma _2)$
.
Proof This is a direct consequence of Theorem 4.1
(d), Theorem 4.3
(b), and the fact that
![]() $\mathrm {GPHP}(\Sigma _\ell )$
implies
$\mathrm {GPHP}(\Sigma _\ell )$
implies
![]() $\mathrm {C}\Sigma _\ell $
.
$\mathrm {C}\Sigma _\ell $
.
Remark. Let the usual relativization of
![]() $\mathrm {IB}$
, namely
$\mathrm {IB}$
, namely
![]() $\forall X\,(\mathrm {I} \Sigma _k(X) \Rightarrow \mathrm {B} \Sigma _{k+1}(X))$
for each k, be called “strong,” and let the “weak” relativization of
$\forall X\,(\mathrm {I} \Sigma _k(X) \Rightarrow \mathrm {B} \Sigma _{k+1}(X))$
for each k, be called “strong,” and let the “weak” relativization of
![]() $\mathrm {IB}$
consist of the statements
$\mathrm {IB}$
consist of the statements
![]() $\mathrm {I}\Sigma ^0_k \Rightarrow \mathrm {B} \Sigma ^0_{k+1}$
for each k. In Theorem 3.7, we showed that
$\mathrm {I}\Sigma ^0_k \Rightarrow \mathrm {B} \Sigma ^0_{k+1}$
for each k. In Theorem 3.7, we showed that
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^3_2$
implies strong relativized
$\mathrm {RCA}^*_0 + \mathrm {RT}^3_2$
implies strong relativized
![]() $\mathrm {IB}$
. On the other hand, Theorem 4.3 implies that already weak relativized
$\mathrm {IB}$
. On the other hand, Theorem 4.3 implies that already weak relativized
![]() $\mathrm {IB}$
, and even its restriction to
$\mathrm {IB}$
, and even its restriction to
![]() $k < \ell $
, suffices to prove
$k < \ell $
, suffices to prove
![]() $\mathrm {GPHP}(\Sigma _\ell )$
.
$\mathrm {GPHP}(\Sigma _\ell )$
.
This lets us prove Corollary 4.4 by exploiting the fact that
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
implies the restriction of weak relativized
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
implies the restriction of weak relativized
![]() $\mathrm {IB}$
to
$\mathrm {IB}$
to
![]() $k = 0,1$
.
$k = 0,1$
.
The known relationships between the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
and fragments of first-order arithmetic are summarized in the following corollary.
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
and fragments of first-order arithmetic are summarized in the following corollary.
Corollary 4.5. The first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
follow from
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
follow from
![]() $\mathrm {I} \Sigma _2$
. The
$\mathrm {I} \Sigma _2$
. The
![]() $\Pi _3$
consequences coincide with
$\Pi _3$
consequences coincide with
![]() $\mathrm {B} \Sigma _1 + \exp $
. The
$\mathrm {B} \Sigma _1 + \exp $
. The
![]() $\Pi _4$
consequences are strictly weaker than
$\Pi _4$
consequences are strictly weaker than
![]() $\mathrm {B} \Sigma _2$
but do not follow from
$\mathrm {B} \Sigma _2$
but do not follow from
![]() $\mathrm {I} \Sigma _1$
.
$\mathrm {I} \Sigma _1$
.
Proof The provability from
![]() $\mathrm {I}\Sigma _2$
is part (b) of Theorem 4.1. The fact that the
$\mathrm {I}\Sigma _2$
is part (b) of Theorem 4.1. The fact that the
![]() $\Pi _3$
consequences of
$\Pi _3$
consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
coincide with
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
coincide with
![]() $\mathrm {B} \Sigma _1 + \exp $
and that the
$\mathrm {B} \Sigma _1 + \exp $
and that the
![]() $\Pi _4$
consequences are strictly weaker than
$\Pi _4$
consequences are strictly weaker than
![]() $\mathrm {B} \Sigma _2$
is proved like in Theorem 3.7. Finally, Corollary 4.4 implies that
$\mathrm {B} \Sigma _2$
is proved like in Theorem 3.7. Finally, Corollary 4.4 implies that
![]() $\mathrm {C}\Sigma _2$
is an example of a
$\mathrm {C}\Sigma _2$
is an example of a
![]() $\Pi _4$
sentence that follows from
$\Pi _4$
sentence that follows from
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
but not
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
but not
![]() $\mathrm {I}\Sigma _1$
.
$\mathrm {I}\Sigma _1$
.
Of course, quite a few questions remain. Over
![]() $\mathrm {B}\Sigma _2$
, one basic issue is whether the first-order consequences of
$\mathrm {B}\Sigma _2$
, one basic issue is whether the first-order consequences of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2 + \mathrm {B}\Sigma _2$
are non-trivial, and another is how closely related they are to those of
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2 + \mathrm {B}\Sigma _2$
are non-trivial, and another is how closely related they are to those of
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
.
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
.
Question 2. Is
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2 + \mathrm {B}\Sigma _2$
conservative over
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2 + \mathrm {B}\Sigma _2$
conservative over
![]() $\mathrm {B}\Sigma _2$
?
$\mathrm {B}\Sigma _2$
?
Question 3. Does
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2 + \mathrm {B}\Sigma _2$
imply
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2 + \mathrm {B}\Sigma _2$
imply
![]() $\psi \lor \Delta _2\textrm {-}\mathrm {RT}^2_2$
for each first-order
$\psi \lor \Delta _2\textrm {-}\mathrm {RT}^2_2$
for each first-order
![]() $\psi $
provable in
$\psi $
provable in
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
?
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
?
Over
![]() $\mathrm {I}\Sigma _1$
, the basic question is:
$\mathrm {I}\Sigma _1$
, the basic question is:
Question 4. Does
![]() $\mathrm {RCA}^*_0 +\mathrm {RT}^2_2 + \mathrm {I}\Sigma _1$
imply
$\mathrm {RCA}^*_0 +\mathrm {RT}^2_2 + \mathrm {I}\Sigma _1$
imply
![]() $\mathrm {B}\Sigma _2$
?
$\mathrm {B}\Sigma _2$
?
We have no strong reasons to believe that the answer is “yes.” However, it should be pointed out that, since
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
proves
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
proves
![]() $\mathrm {B}\Sigma _2$
, answering “no” would involve constructing a model of
$\mathrm {B}\Sigma _2$
, answering “no” would involve constructing a model of
![]() $\mathrm {I}\Sigma _1+\neg \mathrm {B}\Sigma _2$
that expands to a model of
$\mathrm {I}\Sigma _1+\neg \mathrm {B}\Sigma _2$
that expands to a model of
![]() $\mathrm {B}\Sigma ^0_1 + \neg \mathrm {I}\Sigma ^0_1$
– in the terminology of [Reference Kossak23], a model of
$\mathrm {B}\Sigma ^0_1 + \neg \mathrm {I}\Sigma ^0_1$
– in the terminology of [Reference Kossak23], a model of
![]() $\mathrm {I}\Sigma _1+\neg \mathrm {B}\Sigma _2$
that is not always semiregular. The existence of such a model itself seems to be open.
$\mathrm {I}\Sigma _1+\neg \mathrm {B}\Sigma _2$
that is not always semiregular. The existence of such a model itself seems to be open.
Question 5. Does there exist a model
![]() $M \models \mathrm {I}\Sigma _1 + \neg \mathrm {B}\Sigma _2$
that can be expanded to a model
$M \models \mathrm {I}\Sigma _1 + \neg \mathrm {B}\Sigma _2$
that can be expanded to a model
![]() $(M,A) \models \mathrm {B}\Sigma _1(A) + \neg \mathrm {I}\Sigma _1(A)$
?
$(M,A) \models \mathrm {B}\Sigma _1(A) + \neg \mathrm {I}\Sigma _1(A)$
?
Note that if there is M witnessing a positive answer to this question such that
![]() $\mathrm {I}\Sigma _1(A)$
fails in the expansion due to
$\mathrm {I}\Sigma _1(A)$
fails in the expansion due to
![]() $\omega $
being
$\omega $
being
![]() $\Sigma _1(A)$
-definable, then by Theorems 2.3 and 3.7 it has to be the case that
$\Sigma _1(A)$
-definable, then by Theorems 2.3 and 3.7 it has to be the case that
![]() $(\omega ,\mathrm {SSy}(M)) \not \models \mathrm {ACA}_0$
.
$(\omega ,\mathrm {SSy}(M)) \not \models \mathrm {ACA}_0$
.
5 Relativizing Ramsey
In this final section, we take up the question whether our results on
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
shed any light on the problem of characterizing the first-order consequences of
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
shed any light on the problem of characterizing the first-order consequences of
![]() $\mathrm {RCA}_0 +\mathrm {RT}^2_2$
. To this end, we introduce a principle in which both the instances and solutions to Ramsey’s Theorem are allowed to be
$\mathrm {RCA}_0 +\mathrm {RT}^2_2$
. To this end, we introduce a principle in which both the instances and solutions to Ramsey’s Theorem are allowed to be
![]() $\Delta ^0_2$
-sets rather than sets.
$\Delta ^0_2$
-sets rather than sets.
Definition 5.1.
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
is the
$\mathrm {RT}^2_2$
is the
![]() $\Pi ^1_2$
statement: “for every
$\Pi ^1_2$
statement: “for every
![]() $\Delta ^0_2$
-set f which is a
$\Delta ^0_2$
-set f which is a
![]() $2$
-colouring of
$2$
-colouring of
![]() $[\mathbb {N}]^2$
, there exists an infinite homogeneous
$[\mathbb {N}]^2$
, there exists an infinite homogeneous
![]() $\Delta ^0_2$
-set.”
$\Delta ^0_2$
-set.”
Note that
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
is a genuine
$\mathrm {RT}^2_2$
is a genuine
![]() $\Pi ^1_2$
statement, which should not be confused with the
$\Pi ^1_2$
statement, which should not be confused with the
![]() $\Pi ^1_1$
statement relativizing
$\Pi ^1_1$
statement relativizing
![]() $\Delta _2$
-
$\Delta _2$
-
![]() $\mathrm {RT}^2_2$
, namely “for every set X,
$\mathrm {RT}^2_2$
, namely “for every set X,
![]() $\Delta _2(X)$
-
$\Delta _2(X)$
-
![]() $\mathrm {RT}^2_2$
holds.” Of course, in a model of the form
$\mathrm {RT}^2_2$
holds.” Of course, in a model of the form
![]() $(M, \Delta _1\textrm {-}\mathrm {Def}(M))$
, the statement
$(M, \Delta _1\textrm {-}\mathrm {Def}(M))$
, the statement
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
will be equivalent to
$\mathrm {RT}^2_2$
will be equivalent to
![]() $\Delta _2$
-
$\Delta _2$
-
![]() $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
.
We are interested in studying
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
over
$\mathrm {RT}^2_2$
over
![]() $\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$
, especially in the case where
$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$
, especially in the case where
![]() $\mathrm {I} \Sigma ^0_2$
fails. The following proposition shows that in such a context,
$\mathrm {I} \Sigma ^0_2$
fails. The following proposition shows that in such a context,
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
behaves somewhat analogously to
$\mathrm {RT}^2_2$
behaves somewhat analogously to
![]() $\mathrm {RT}^2_2$
over
$\mathrm {RT}^2_2$
over
![]() ${\mathrm {RCA}^*_0}$
, so we can investigate it using the methods developed in Sections 2–4.
${\mathrm {RCA}^*_0}$
, so we can investigate it using the methods developed in Sections 2–4.
Lemma 5.2. For any model
![]() $(M,\mathcal {X}) \models \mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$
,
$(M,\mathcal {X}) \models \mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$
,
![]() $(M,\mathcal {X}) \models \Delta ^0_2$
-
$(M,\mathcal {X}) \models \Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
iff
$\mathrm {RT}^2_2$
iff
![]() $(M, \Delta ^0_2\textrm {-}\mathrm {Def}(M,\mathcal {X})) \models \mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
. As a consequence:
$(M, \Delta ^0_2\textrm {-}\mathrm {Def}(M,\mathcal {X})) \models \mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
. As a consequence:
-
(a) If I is a
 $\Sigma ^0_2$
-definable proper cut in
$\Sigma ^0_2$
-definable proper cut in
 $(M,\mathcal {X})$
, then
$(M,\mathcal {X})$
, then
 $(M,\mathcal {X}) \models \Delta ^0_2$
-
$(M,\mathcal {X}) \models \Delta ^0_2$
-
 $\mathrm {RT}^2_2$
iff
$\mathrm {RT}^2_2$
iff
 ${(I,\mathrm {Cod}(M/I))}\models \mathrm {RT}^2_2$
.
${(I,\mathrm {Cod}(M/I))}\models \mathrm {RT}^2_2$
. -
(b) The first-order consequences of
 ${\mathrm {RCA}_0} + {\mathrm {B}\Sigma _2} + {\neg \mathrm {I}\Sigma _2} + {\Delta ^0_2}$
-
${\mathrm {RCA}_0} + {\mathrm {B}\Sigma _2} + {\neg \mathrm {I}\Sigma _2} + {\Delta ^0_2}$
-
 $\mathrm {RT}^2_2$
are axiomatized by
$\mathrm {RT}^2_2$
are axiomatized by
 $\mathrm {B}\Sigma _2 + \Delta _2$
-
$\mathrm {B}\Sigma _2 + \Delta _2$
-
 $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
. -
(c)
 $\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2 + \Delta ^0_2$
-
$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2 + \Delta ^0_2$
-
 $\mathrm {RT}^2_2$
is
$\mathrm {RT}^2_2$
is
 $\Pi _4$
- but not
$\Pi _4$
- but not
 $\Pi _5$
-conservative over
$\Pi _5$
-conservative over
 $\mathrm {B}\Sigma _2$
.
$\mathrm {B}\Sigma _2$
.
Proof The fact that a model
![]() $(M,\mathcal {X})$
satisfies
$(M,\mathcal {X})$
satisfies
![]() $\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2 + \Delta ^0_2$
-
$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2 + \Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
exactly if
$\mathrm {RT}^2_2$
exactly if
![]() $(M, \Delta ^0_2\textrm {-}\mathrm {Def}(M,\mathcal {X})) \models \mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
is immediate from the definitions. Thus (a) follows from Theorem 2.3, because a cut I is
$(M, \Delta ^0_2\textrm {-}\mathrm {Def}(M,\mathcal {X})) \models \mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
is immediate from the definitions. Thus (a) follows from Theorem 2.3, because a cut I is
![]() $\Sigma ^0_2$
definable in
$\Sigma ^0_2$
definable in
![]() $(M,\mathcal {X}) \models \mathrm {B}\Sigma ^0_2$
exactly if it is
$(M,\mathcal {X}) \models \mathrm {B}\Sigma ^0_2$
exactly if it is
![]() $\Sigma ^0_1$
-definable in
$\Sigma ^0_1$
-definable in
![]() $(M, \Delta ^0_2\textrm {-}\mathrm {Def}(M,\mathcal {X}))$
.
$(M, \Delta ^0_2\textrm {-}\mathrm {Def}(M,\mathcal {X}))$
.
To prove (b), repeat the argument from the proof of Theorem 4.1
(a), relativizing it to
![]() $0'$
. If
$0'$
. If
![]() $M \models \mathrm {B} \Sigma _2 + \Delta _2$
-
$M \models \mathrm {B} \Sigma _2 + \Delta _2$
-
![]() $\mathrm {RT}^2_2$
, then
$\mathrm {RT}^2_2$
, then
![]() $(M, \Delta _1\textrm {-}\mathrm {Def}(M)) \models {\mathrm {RCA}_0} + {\mathrm {B}\Sigma _2} + {\neg \mathrm {I}\Sigma _2} + {\Delta ^0_2}$
-
$(M, \Delta _1\textrm {-}\mathrm {Def}(M)) \models {\mathrm {RCA}_0} + {\mathrm {B}\Sigma _2} + {\neg \mathrm {I}\Sigma _2} + {\Delta ^0_2}$
-
![]() $\mathrm {RT}^2_2$
. In the other direction, if
$\mathrm {RT}^2_2$
. In the other direction, if
![]() $(M, \mathcal {X}) \models {\mathrm {RCA}_0} + {\mathrm {B}\Sigma _2} + {\neg \mathrm {I}\Sigma _2} + {\Delta ^0_2}$
-
$(M, \mathcal {X}) \models {\mathrm {RCA}_0} + {\mathrm {B}\Sigma _2} + {\neg \mathrm {I}\Sigma _2} + {\Delta ^0_2}$
-
![]() $\mathrm {RT}^2_2$
and I is a proper
$\mathrm {RT}^2_2$
and I is a proper
![]() $\Sigma _2$
-definable cut in M, then two applications of (a) give first
$\Sigma _2$
-definable cut in M, then two applications of (a) give first
![]() ${(I,\mathrm {Cod}(M/I))}\models \mathrm {RT}^2_2$
and then
${(I,\mathrm {Cod}(M/I))}\models \mathrm {RT}^2_2$
and then
![]() $(M, \Delta _1\textrm {-}\mathrm {Def}(M)) \models \Delta ^0_2$
-
$(M, \Delta _1\textrm {-}\mathrm {Def}(M)) \models \Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
, but the latter is equivalent to
$\mathrm {RT}^2_2$
, but the latter is equivalent to
![]() $M \models \Delta _2$
-
$M \models \Delta _2$
-
![]() $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
.
To show that
![]() ${\mathrm {RCA}_0} + {\mathrm {B}\Sigma ^0_2} + {\Delta ^0_2}$
-
${\mathrm {RCA}_0} + {\mathrm {B}\Sigma ^0_2} + {\Delta ^0_2}$
-
![]() $\mathrm {RT}^2_2$
is
$\mathrm {RT}^2_2$
is
![]() $\Pi _4$
-conservative over
$\Pi _4$
-conservative over
![]() $\mathrm {B}\Sigma _2$
, relativize to
$\mathrm {B}\Sigma _2$
, relativize to
![]() $0'$
the argument used to prove
$0'$
the argument used to prove
![]() $\Pi _3$
-conservativity of
$\Pi _3$
-conservativity of
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
over
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_2$
over
![]() $\mathrm {B}\Sigma _1+ \exp $
in Theorem 3.7
(b). To show lack of
$\mathrm {B}\Sigma _1+ \exp $
in Theorem 3.7
(b). To show lack of
![]() $\Pi _5$
-conservativity, consider the sentence
$\Pi _5$
-conservativity, consider the sentence
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2$
-
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2$
-
![]() $\mathrm {RT}^2_2$
. This is a
$\mathrm {RT}^2_2$
. This is a
![]() $\Pi _5$
statement, and it is provable in
$\Pi _5$
statement, and it is provable in
![]() ${\mathrm {RCA}_0} + {\mathrm {B}\Sigma ^0_2} + {\Delta ^0_2}$
-
${\mathrm {RCA}_0} + {\mathrm {B}\Sigma ^0_2} + {\Delta ^0_2}$
-
![]() $\mathrm {RT}^2_2$
by (b). On the other hand, it is not provable in
$\mathrm {RT}^2_2$
by (b). On the other hand, it is not provable in
![]() $\mathrm {B}\Sigma _2$
, as can be seen by applying (a) to any model
$\mathrm {B}\Sigma _2$
, as can be seen by applying (a) to any model
![]() $M \models \mathrm {B} \Sigma _2$
with
$M \models \mathrm {B} \Sigma _2$
with
![]() $\Sigma _2$
-definable
$\Sigma _2$
-definable
![]() $\omega $
and
$\omega $
and
![]() $(\omega , \mathrm {SSy}(M)) \not \models \mathrm {RT}^2_2$
. This proves (c).
$(\omega , \mathrm {SSy}(M)) \not \models \mathrm {RT}^2_2$
. This proves (c).
Since Lemma 5.2 shows that
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
is not
$\mathrm {RT}^2_2$
is not
![]() $\Pi _5$
-conservative over
$\Pi _5$
-conservative over
![]() $\mathrm {B}\Sigma _2$
, while the conservativity of
$\mathrm {B}\Sigma _2$
, while the conservativity of
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
over
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
over
![]() $\mathrm {B}\Sigma _2$
is a well-known open problem, it is natural to ask whether
$\mathrm {B}\Sigma _2$
is a well-known open problem, it is natural to ask whether
![]() $\mathrm {RT}^2_2$
might imply
$\mathrm {RT}^2_2$
might imply
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
, at least in the particularly relevant setting of models of
$\mathrm {RT}^2_2$
, at least in the particularly relevant setting of models of
![]() $\mathrm {B}\Sigma ^0_2 + \neg \mathrm {I} \Sigma ^0_2$
.
$\mathrm {B}\Sigma ^0_2 + \neg \mathrm {I} \Sigma ^0_2$
.
In Theorem 5.4, we show a negative result: there is no implication in either direction, and the sentence we used to prove lack of
![]() $\Pi _5$
-conservativity of
$\Pi _5$
-conservativity of
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
is unprovable in
$\mathrm {RT}^2_2$
is unprovable in
![]() $\mathrm {RT}^2_2$
. To prove this, we will have to make use of a connection between properties of infinite
$\mathrm {RT}^2_2$
. To prove this, we will have to make use of a connection between properties of infinite
![]() $\Delta _2$
-sets and the consistency of
$\Delta _2$
-sets and the consistency of
![]() $\mathrm {I} \Sigma _1$
that may probably be considered folklore, but for which we did not find a suitable reference. So, we state the connection as a separate lemma and sketch its proof in Section 6.
$\mathrm {I} \Sigma _1$
that may probably be considered folklore, but for which we did not find a suitable reference. So, we state the connection as a separate lemma and sketch its proof in Section 6.
Lemma 5.3. There exists a polynomial p such that
![]() $\mathrm {I}\Sigma _1$
proves:
$\mathrm {I}\Sigma _1$
proves:
where
![]() $\mathrm {Con}_{x}(T)$
means that there is no inconsistency proof in T containing fewer than x symbols.
$\mathrm {Con}_{x}(T)$
means that there is no inconsistency proof in T containing fewer than x symbols.
It may be worth pointing out that Lemma 5.3 is a quantitative version of a weakening of the well-known fact that
![]() $\mathrm {I}\Sigma _2$
is equivalent to uniform
$\mathrm {I}\Sigma _2$
is equivalent to uniform
![]() $\Pi _4$
-reflection for
$\Pi _4$
-reflection for
![]() $\mathrm {I} \Delta _0 + \exp $
(see, e.g., [Reference Beklemishev1, Theorem 7]). To see this, note that (over
$\mathrm {I} \Delta _0 + \exp $
(see, e.g., [Reference Beklemishev1, Theorem 7]). To see this, note that (over
![]() $\mathrm {I}\Delta _0 + \exp $
as a base theory)
$\mathrm {I}\Delta _0 + \exp $
as a base theory)
![]() $\mathrm {I} \Sigma _2$
is equivalent to the statement that each infinite
$\mathrm {I} \Sigma _2$
is equivalent to the statement that each infinite
![]() $\Delta _2$
-set contains arbitrarily large finite sets, while
$\Delta _2$
-set contains arbitrarily large finite sets, while
![]() $\Pi _4$
-reflection for
$\Pi _4$
-reflection for
![]() $\mathrm {I} \Delta _0 + \exp $
implies
$\mathrm {I} \Delta _0 + \exp $
implies
![]() $\mathrm {Con}(\mathrm {I}\Sigma _1)$
.
$\mathrm {Con}(\mathrm {I}\Sigma _1)$
.
Theorem 5.4.
![]() $\mathrm {RT}^2_2$
and
$\mathrm {RT}^2_2$
and
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
are incomparable over
$\mathrm {RT}^2_2$
are incomparable over
![]() $\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2 + \neg \mathrm {I} \Sigma ^0_2$
. Moreover,
$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2 + \neg \mathrm {I} \Sigma ^0_2$
. Moreover,
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
does not prove
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
does not prove
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2$
-
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2$
-
![]() $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
.
Proof The fact that
![]() ${\mathrm {RCA}_0} + {\mathrm {B}\Sigma ^0_2} + {\neg \mathrm {I} \Sigma ^0_2} + {\Delta ^0_2}$
-
${\mathrm {RCA}_0} + {\mathrm {B}\Sigma ^0_2} + {\neg \mathrm {I} \Sigma ^0_2} + {\Delta ^0_2}$
-
![]() $\mathrm {RT}^2_2$
does not prove
$\mathrm {RT}^2_2$
does not prove
![]() $\mathrm {RT}^2_2$
is witnessed by any structure of the form
$\mathrm {RT}^2_2$
is witnessed by any structure of the form
![]() $(M, \Delta _1\textrm {-}\mathrm {Def}(M))$
, where
$(M, \Delta _1\textrm {-}\mathrm {Def}(M))$
, where
![]() $M \models \mathrm {B} \Sigma _2$
has
$M \models \mathrm {B} \Sigma _2$
has
![]() $\Sigma _2$
-definable
$\Sigma _2$
-definable
![]() $\omega $
and
$\omega $
and
![]() $(\omega ,\mathrm {SSy}(M)) \models \mathrm {RT}^2_2$
. By Lemma 5.2
(a), such a structure satisfies
$(\omega ,\mathrm {SSy}(M)) \models \mathrm {RT}^2_2$
. By Lemma 5.2
(a), such a structure satisfies
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
, but by Lemma 3.3
(a) it cannot satisfy
$\mathrm {RT}^2_2$
, but by Lemma 3.3
(a) it cannot satisfy
![]() $\mathrm {RT}^2_2$
.
$\mathrm {RT}^2_2$
.
In the other direction, such a “quick and dirty” argument does not seem to be currently available: of the known constructions producing models of
![]() ${\mathrm {RCA}_0} + {\mathrm {RT}^2_2} + {\neg \mathrm {I}\Sigma ^0_2}$
, that of [Reference Chong, Slaman and Yang6, Reference Chong, Slaman and Yang7] involves strong constraints on
${\mathrm {RCA}_0} + {\mathrm {RT}^2_2} + {\neg \mathrm {I}\Sigma ^0_2}$
, that of [Reference Chong, Slaman and Yang6, Reference Chong, Slaman and Yang7] involves strong constraints on
![]() $\mathrm {SSy}(M)$
, and that of [Reference Kołodziejczyk and Yokoyama22, Reference Patey and Yokoyama27] does not give a
$\mathrm {SSy}(M)$
, and that of [Reference Kołodziejczyk and Yokoyama22, Reference Patey and Yokoyama27] does not give a
![]() $\Sigma ^0_2$
-definable
$\Sigma ^0_2$
-definable
![]() $\omega $
. To show that
$\omega $
. To show that
![]() ${\mathrm {RCA}_0} + {\mathrm {RT}^2_2} + {\neg \mathrm {I} \Sigma ^0_2}$
does not imply
${\mathrm {RCA}_0} + {\mathrm {RT}^2_2} + {\neg \mathrm {I} \Sigma ^0_2}$
does not imply
![]() $\Delta ^0_2$
-
$\Delta ^0_2$
-
![]() $\mathrm {RT}^2_2$
, it is enough to prove the “Moreover” part of the statement, namely:
$\mathrm {RT}^2_2$
, it is enough to prove the “Moreover” part of the statement, namely:
This we do by means of a proof speedup argument. By [Reference Kołodziejczyk, Wong and Yokoyama20, Lemma 3.2],
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
proves the statement “for every k, if every infinite set contains at least k elements, then every infinite set contains at least
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
proves the statement “for every k, if every infinite set contains at least k elements, then every infinite set contains at least
![]() $2^k$
elements.” It follows immediately that
$2^k$
elements.” It follows immediately that
![]() $\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
proves “for every k, if every infinite
$\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
proves “for every k, if every infinite
![]() $\Delta _2$
-set contains at least k elements, then every infinite
$\Delta _2$
-set contains at least k elements, then every infinite
![]() $\Delta _2$
-set contains at least
$\Delta _2$
-set contains at least
![]() $2^k$
elements.” This implies that the definable set
$2^k$
elements.” This implies that the definable set
is a cut in
![]() $\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
. This in turn implies (cf. [Reference Pudlák and Buss28, Theorem 3.4.1]) that, for each
$\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
. This in turn implies (cf. [Reference Pudlák and Buss28, Theorem 3.4.1]) that, for each
![]() $n \in \omega $
, there is a
$n \in \omega $
, there is a
![]() $\mathrm {poly}(n)$
-size proof of
$\mathrm {poly}(n)$
-size proof of
in
![]() $\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
. But by Lemma 5.3 and the fact that the exponential function dominates every polynomial,
$\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
. But by Lemma 5.3 and the fact that the exponential function dominates every polynomial,
![]() $\mathrm {I} \Sigma _1$
proves:
$\mathrm {I} \Sigma _1$
proves:
 $$ \begin{align*} &\forall x\ \big{[}\textrm{"every infinite } \Delta_2 \textrm{-set contains at least } \exp_{\exp_{x+1}(2)}{(2)} \textrm{ elements"}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Rightarrow \mathrm{Con}_{\exp_x(2)}(\mathrm{I} \Sigma_1) \big{]}. \end{align*} $$
$$ \begin{align*} &\forall x\ \big{[}\textrm{"every infinite } \Delta_2 \textrm{-set contains at least } \exp_{\exp_{x+1}(2)}{(2)} \textrm{ elements"}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Rightarrow \mathrm{Con}_{\exp_x(2)}(\mathrm{I} \Sigma_1) \big{]}. \end{align*} $$
Thus, for each standard n there is a
![]() $\mathrm {poly}(n)$
-size proof of
$\mathrm {poly}(n)$
-size proof of
![]() $\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
$\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
![]() $\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
.
$\mathrm {B} \Sigma _2 + \Delta _2\textrm {-}\mathrm {RT}^2_2$
.
Reasoning by cases, we can show that also
![]() ${\mathrm {B} \Sigma _2} + {(\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2)}$
proves
${\mathrm {B} \Sigma _2} + {(\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2)}$
proves
![]() $\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
$\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
![]() $\mathrm {poly}(n)$
-size. Indeed, either
$\mathrm {poly}(n)$
-size. Indeed, either
![]() $\mathrm {I} \Sigma _2$
holds, in which case we simply have
$\mathrm {I} \Sigma _2$
holds, in which case we simply have
![]() $\mathrm {Con}(\mathrm {I} \Sigma _1)$
, or
$\mathrm {Con}(\mathrm {I} \Sigma _1)$
, or
![]() $\mathrm {I} \Sigma _2$
fails, in which case we have
$\mathrm {I} \Sigma _2$
fails, in which case we have
![]() $\Delta _2\textrm {-}\mathrm {RT}^2_2$
and we can use the proof of
$\Delta _2\textrm {-}\mathrm {RT}^2_2$
and we can use the proof of
![]() $\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
mentioned in the previous paragraph.
$\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
mentioned in the previous paragraph.
However, the size of the smallest proof of
![]() $\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
$\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
![]() $\mathrm {I} \Sigma _1$
grows nonelementarily in n [Reference Pudlák and Buss28, Theorem 7.2.2], and by [Reference Kołodziejczyk, Wong and Yokoyama20],
$\mathrm {I} \Sigma _1$
grows nonelementarily in n [Reference Pudlák and Buss28, Theorem 7.2.2], and by [Reference Kołodziejczyk, Wong and Yokoyama20],
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
has no superpolynomial proof speedup over
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
has no superpolynomial proof speedup over
![]() $\mathrm {I} \Sigma _1$
w.r.t. proofs of
$\mathrm {I} \Sigma _1$
w.r.t. proofs of
![]() $\Pi _3$
sentences. Thus, the size of the smallest proof of
$\Pi _3$
sentences. Thus, the size of the smallest proof of
![]() $\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
$\mathrm {Con}_{\exp _n(2)}(\mathrm {I} \Sigma _1)$
in
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
also grows nonelementarily in n. Since
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
also grows nonelementarily in n. Since
![]() $\mathrm {B} \Sigma _2 + (\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2)$
is axiomatized by a single sentence, and
$\mathrm {B} \Sigma _2 + (\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2)$
is axiomatized by a single sentence, and
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
proves
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
proves
![]() $\mathrm {B} \Sigma _2$
, it follows that it cannot prove
$\mathrm {B} \Sigma _2$
, it follows that it cannot prove
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
.
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
.
Thus, the statement
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
cannot be used to witness the potential nonconservativity of
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
cannot be used to witness the potential nonconservativity of
![]() $\mathrm {RT}^2_2$
over
$\mathrm {RT}^2_2$
over
![]() $\mathrm {B}\Sigma _2$
. However, our argument for this, in addition to being somewhat roundabout, made use of the fact that
$\mathrm {B}\Sigma _2$
. However, our argument for this, in addition to being somewhat roundabout, made use of the fact that
![]() $\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
proves “for every k, if every infinite set contains at least k elements, then every infinite set contains at least
$\mathrm {RCA}^*_0 + \mathrm {RT}^2_2$
proves “for every k, if every infinite set contains at least k elements, then every infinite set contains at least
![]() $2^k$
elements,” which is shown using exponential lower bounds on finite Ramsey numbers. Thus the argument is no longer applicable to various apparently slight weakenings of
$2^k$
elements,” which is shown using exponential lower bounds on finite Ramsey numbers. Thus the argument is no longer applicable to various apparently slight weakenings of
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
, for instance to statements in which
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
, for instance to statements in which
![]() $\mathrm {RT}^2_2$
is replaced by a restriction to colourings for which finite Ramsey numbers are polynomial.
$\mathrm {RT}^2_2$
is replaced by a restriction to colourings for which finite Ramsey numbers are polynomial.
As an illustration, we mention two weakenings of
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
whose status is open and seems intriguing.
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {RT}^2_2$
whose status is open and seems intriguing.
Question 6. Does
![]() $\mathrm {RCA}_0 + \mathrm {RT}^2_2$
prove one of the following
$\mathrm {RCA}_0 + \mathrm {RT}^2_2$
prove one of the following
![]() $\Pi _5$
statements:
$\Pi _5$
statements:
-
(a)
 $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {CAC}$
: if
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {CAC}$
: if
 $\neg \mathrm {I} \Sigma _2$
, then every
$\neg \mathrm {I} \Sigma _2$
, then every
 $\Delta _2$
-definable partial order on
$\Delta _2$
-definable partial order on
 $[\mathbb {N}]$
contains an infinite
$[\mathbb {N}]$
contains an infinite
 $\Delta _2$
-definable chain or an infinite
$\Delta _2$
-definable chain or an infinite
 $\Delta _2$
-definable antichain.”
$\Delta _2$
-definable antichain.” -
(b) “If
 $\neg \mathrm {I} \Sigma _2$
, then for every
$\neg \mathrm {I} \Sigma _2$
, then for every
 $\Delta _1$
-definable
$\Delta _1$
-definable
 $2$
-colouring of
$2$
-colouring of
 $[\mathbb {N}]^2$
there is a
$[\mathbb {N}]^2$
there is a
 $\Delta _2$
-definable infinite homogeneous set?”
$\Delta _2$
-definable infinite homogeneous set?”
Does
![]() $\mathrm {RCA}_0 + \mathrm {B} \Sigma ^0_2$
prove the statement in (b)?
$\mathrm {RCA}_0 + \mathrm {B} \Sigma ^0_2$
prove the statement in (b)?
The fact that
![]() $\mathrm {RCA}_{0} + \mathrm {B} \Sigma ^0_2$
does not prove the statement
$\mathrm {RCA}_{0} + \mathrm {B} \Sigma ^0_2$
does not prove the statement
![]() $\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {CAC}$
appearing in (a) can be shown using the methods of [Reference Fiori-Carones, Kołodziejczyk and Kowalik11].
$\neg \mathrm {I}\Sigma _2 \Rightarrow \Delta _2\textrm {-}\mathrm {CAC}$
appearing in (a) can be shown using the methods of [Reference Fiori-Carones, Kołodziejczyk and Kowalik11].
6 Proof of Lemma 5.3
Lemma 5.3. There exists a polynomial p such that
![]() $\mathrm {I}\Sigma _1$
proves:
$\mathrm {I}\Sigma _1$
proves:
where
![]() $\mathrm {Con}_{x}(T)$
means that there is no inconsistency proof in T containing fewer than x symbols.
$\mathrm {Con}_{x}(T)$
means that there is no inconsistency proof in T containing fewer than x symbols.
Proof We assume that our proof system is a Tait-style calculus (see, e.g., [Reference Beklemishev1, Section 4.1]). Thus,
![]() $\land , \lor , \neg $
are our only connectives, with
$\land , \lor , \neg $
are our only connectives, with
![]() $\neg $
allowed to appear explicitly only in front of atoms and negation otherwise defined recursively using the De Morgan laws. The proof lines are cedents, or finite sets of formulas interpreted as disjunctions. The logical axioms are cedents of the form
$\neg $
allowed to appear explicitly only in front of atoms and negation otherwise defined recursively using the De Morgan laws. The proof lines are cedents, or finite sets of formulas interpreted as disjunctions. The logical axioms are cedents of the form
![]() $\Gamma , \psi , \neg \psi $
for
$\Gamma , \psi , \neg \psi $
for
![]() $\psi $
atomic, as well as analogous cedents corresponding to the equality axioms (the need to allow the arbitrary set of formulas
$\psi $
atomic, as well as analogous cedents corresponding to the equality axioms (the need to allow the arbitrary set of formulas
![]() $\Gamma $
to appear in axioms arises because there is no weakening rule). The most important rules from our perspective are the rules for introducing conjunctions and quantifiers:
$\Gamma $
to appear in axioms arises because there is no weakening rule). The most important rules from our perspective are the rules for introducing conjunctions and quantifiers:

where in the
![]() $(\exists )$
rule t must be a term that is substitutable for
$(\exists )$
rule t must be a term that is substitutable for
![]() $w $
in
$w $
in
![]() $\psi $
, and in the
$\psi $
, and in the
![]() $(\forall )$
rule a must be an eigenvariable, i.e., a free variable that does not appear anywhere in the conclusion of the rule. There are also natural disjunction introduction rules and the cut rule.
$(\forall )$
rule a must be an eigenvariable, i.e., a free variable that does not appear anywhere in the conclusion of the rule. There are also natural disjunction introduction rules and the cut rule.
We may assume that
![]() $\mathrm {I}\Sigma _1$
is axiomatized by finitely many sentences
$\mathrm {I}\Sigma _1$
is axiomatized by finitely many sentences
![]() $\gamma _1,\ldots ,\gamma _n$
, where each
$\gamma _1,\ldots ,\gamma _n$
, where each
![]() $\gamma _i$
has the form
$\gamma _i$
has the form
 $$ \begin{align*} &\forall \bar v\, \exists x\, \exists \bar y\, \forall \bar z\,\forall \bar z'\, \\&\qquad\qquad[x<v_{1}\wedge [\neg\, \delta_i(0, \bar z, \bar v) \lor \delta_i(v_1, \bar y, \bar v) \lor (\delta_{i}(x,\bar y,\bar v) \land \neg\, \delta_i(x\!+\!1,\bar z', \bar v))]], \end{align*} $$
$$ \begin{align*} &\forall \bar v\, \exists x\, \exists \bar y\, \forall \bar z\,\forall \bar z'\, \\&\qquad\qquad[x<v_{1}\wedge [\neg\, \delta_i(0, \bar z, \bar v) \lor \delta_i(v_1, \bar y, \bar v) \lor (\delta_{i}(x,\bar y,\bar v) \land \neg\, \delta_i(x\!+\!1,\bar z', \bar v))]], \end{align*} $$
with
![]() $\delta _i$
bounded. (Using a different finite axiomatization would shorten proofs in
$\delta _i$
bounded. (Using a different finite axiomatization would shorten proofs in
![]() $\mathrm {I}\Sigma _1$
by at most a constant additive factor, and using the typical axiomatization of
$\mathrm {I}\Sigma _1$
by at most a constant additive factor, and using the typical axiomatization of
![]() $\mathrm {I}\Sigma _1$
as a scheme would shorten proofs at most polynomially.)
$\mathrm {I}\Sigma _1$
as a scheme would shorten proofs at most polynomially.)
By the cut elimination theorem, which formalizes in (a fragment of)
![]() $\mathrm {I} \Sigma _1$
, if there is an inconsistency proof from
$\mathrm {I} \Sigma _1$
, if there is an inconsistency proof from
![]() $\mathrm {I} \Sigma _1$
of size at most x, then for some fixed polynomial p there is a cut-free proof of the cedent
$\mathrm {I} \Sigma _1$
of size at most x, then for some fixed polynomial p there is a cut-free proof of the cedent
of size at most
![]() ${\exp _{p(x)}(2)}$
. Working in
${\exp _{p(x)}(2)}$
. Working in
![]() $\mathrm {I} \Sigma _1$
, let k be such that every infinite
$\mathrm {I} \Sigma _1$
, let k be such that every infinite
![]() $\Delta _2$
-set contains at least
$\Delta _2$
-set contains at least
![]() ${\exp _{p(k)}(2)}$
elements. Let m stand for
${\exp _{p(k)}(2)}$
elements. Let m stand for
![]() ${\exp _{p(k)}(2)}$
. We will prove that there is no cut-free proof of
${\exp _{p(k)}(2)}$
. We will prove that there is no cut-free proof of
![]() $\neg \gamma _1,\ldots ,\neg \gamma _n$
of size at most m, which will imply
$\neg \gamma _1,\ldots ,\neg \gamma _n$
of size at most m, which will imply
![]() $\mathrm {Con}_k(\mathrm {I}\Sigma _1)$
.
$\mathrm {Con}_k(\mathrm {I}\Sigma _1)$
.
Assume to the contrary that there is such a cut-free proof, and let the lines of the proof be
![]() $C_1,\ldots ,C_\ell $
; note that
$C_1,\ldots ,C_\ell $
; note that
![]() $\ell \le m$
. For each
$\ell \le m$
. For each
![]() $j = 1, \ldots , \ell $
, let the negations of the formulas in
$j = 1, \ldots , \ell $
, let the negations of the formulas in
![]() $C_j$
be
$C_j$
be
![]() $\xi _{j,1}, \ldots , \xi _{j,r_j}$
. Note that
$\xi _{j,1}, \ldots , \xi _{j,r_j}$
. Note that
![]() $r_\ell = n$
, each
$r_\ell = n$
, each
![]() $\xi _{\ell ,i}$
is
$\xi _{\ell ,i}$
is
![]() $\gamma _i$
, and, by the subformula property of cut-free proofs, each
$\gamma _i$
, and, by the subformula property of cut-free proofs, each
![]() $\xi _{j,r}$
is a subformula of one of the
$\xi _{j,r}$
is a subformula of one of the
![]() $\psi _i$
’s. As usual in such a context, we regard
$\psi _i$
’s. As usual in such a context, we regard
![]() $\varphi (t)$
as a subformula of
$\varphi (t)$
as a subformula of
![]() $\mathrm {Q}x\,\varphi $
for
$\mathrm {Q}x\,\varphi $
for
![]() $\mathrm {Q}$
a quantifier.
$\mathrm {Q}$
a quantifier.
Define an infinite sequence of numbers by:
 $$ \begin{align*} d_0 & = 0, \\ d_{j+1} & = \textrm{least } d> d_j \textrm{ s.t. if } u \textrm{ is the smallest number s.t.~each term} \\ & \ \ \ \ \ \, \textrm{with }{\le}~m \textrm{ symbols evaluated on arguments }{\le}~d_j \textrm{ has value }{\le}~u, \\ & \ \ \ \ \ \, \textrm{then }d \ge u \textrm{ and, for each }i =1,\ldots,n, \textrm{ each } \bar v \textrm{ and } x: \\ & \ \ \ \ \ \, \!\max(x,\max(\bar v)) \le {u} \land \exists \bar y\, \delta_i(x,\bar y, \bar v) \Rightarrow \exists \bar y\,(\max(\bar y) \le d \land \delta_i(x,\bar y, \bar v)). \end{align*} $$
$$ \begin{align*} d_0 & = 0, \\ d_{j+1} & = \textrm{least } d> d_j \textrm{ s.t. if } u \textrm{ is the smallest number s.t.~each term} \\ & \ \ \ \ \ \, \textrm{with }{\le}~m \textrm{ symbols evaluated on arguments }{\le}~d_j \textrm{ has value }{\le}~u, \\ & \ \ \ \ \ \, \textrm{then }d \ge u \textrm{ and, for each }i =1,\ldots,n, \textrm{ each } \bar v \textrm{ and } x: \\ & \ \ \ \ \ \, \!\max(x,\max(\bar v)) \le {u} \land \exists \bar y\, \delta_i(x,\bar y, \bar v) \Rightarrow \exists \bar y\,(\max(\bar y) \le d \land \delta_i(x,\bar y, \bar v)). \end{align*} $$
Let D consist of all numbers that appear as some
![]() $d_j$
. Note that provably in
$d_j$
. Note that provably in
![]() $\mathrm {I} \Sigma _1$
, both D and the complement of D are
$\mathrm {I} \Sigma _1$
, both D and the complement of D are
![]() $\Sigma _2$
-definable, so D is a
$\Sigma _2$
-definable, so D is a
![]() $\Delta _2$
-set, and D is infinite. By our assumption, there exists an
$\Delta _2$
-set, and D is infinite. By our assumption, there exists an
![]() $\ell $
-element finite subset of D. Without loss of generality, we may assume that the elements of this subset are
$\ell $
-element finite subset of D. Without loss of generality, we may assume that the elements of this subset are
![]() $d_0, \ldots , d_{\ell -1}$
.
$d_0, \ldots , d_{\ell -1}$
.
We claim that the following statement
![]() $\eta (s)$
can be proved by
$\eta (s)$
can be proved by
![]() $\Pi _1$
induction on
$\Pi _1$
induction on
![]() $s = 0,\ldots ,\ell \!-\!1$
:
$s = 0,\ldots ,\ell \!-\!1$
:
“There exist
![]() $j \le \ell - s$
and an assignment
$j \le \ell - s$
and an assignment
![]() $\alpha $
of values
$\alpha $
of values
![]() $\le d_{s}$
to the free variables in
$\le d_{s}$
to the free variables in
![]() $C_{j}$
such that, for every
$C_{j}$
such that, for every
![]() $\xi _{j,r}$
that is
$\xi _{j,r}$
that is
![]() $\Sigma _2$
, there is an assignment of values
$\Sigma _2$
, there is an assignment of values
![]() $\le d_{s}$
to the variables (if any) in the unbounded existential quantifier block of
$\le d_{s}$
to the variables (if any) in the unbounded existential quantifier block of
![]() $\xi _{j,r}$
that together with
$\xi _{j,r}$
that together with
![]() $\alpha $
makes the
$\alpha $
makes the
![]() $\Pi _1$
part of
$\Pi _1$
part of
![]() $\xi _{j,r}$
satisfied.”
$\xi _{j,r}$
satisfied.”
Note that
![]() $\eta (s)$
is indeed a
$\eta (s)$
is indeed a
![]() $\Pi _1$
statement (provably in
$\Pi _1$
statement (provably in
![]() $\mathrm {B}\Sigma _1 + \exp $
), because all the quantifiers preceding the definition of satisfaction for
$\mathrm {B}\Sigma _1 + \exp $
), because all the quantifiers preceding the definition of satisfaction for
![]() $\Pi _1$
formulas are bounded. Moreover,
$\Pi _1$
formulas are bounded. Moreover,
![]() $\eta (0)$
is true, because it is witnessed by
$\eta (0)$
is true, because it is witnessed by
![]() $j = \ell $
and the empty assignment, while
$j = \ell $
and the empty assignment, while
![]() $\eta ( \ell -1)$
is false, because
$\eta ( \ell -1)$
is false, because
![]() $C_1$
has to be a logical axiom, so an assignment witnessing the statement at
$C_1$
has to be a logical axiom, so an assignment witnessing the statement at
![]() $j = 1$
would have to satisfy two mutually contradictory quantifier-free formulas or falsify an equality axiom. Therefore, if the induction step goes through for
$j = 1$
would have to satisfy two mutually contradictory quantifier-free formulas or falsify an equality axiom. Therefore, if the induction step goes through for
![]() $\eta (s)$
, we obtain the required contradiction.
$\eta (s)$
, we obtain the required contradiction.
The induction step splits into cases depending on the rule used to derive
![]() $C_j$
, where j witnesses
$C_j$
, where j witnesses
![]() $\eta (s)$
. We consider the nontrivial cases, namely the ones corresponding to
$\eta (s)$
. We consider the nontrivial cases, namely the ones corresponding to
![]() $(\land ), (\exists )$
, and
$(\land ), (\exists )$
, and
![]() $(\forall )$
inferences.
$(\forall )$
inferences.
If
![]() $C_j$
was derived using the
$C_j$
was derived using the
![]() $(\land )$
rule, then
$(\land )$
rule, then
![]() $C_j$
is
$C_j$
is
![]() $\Gamma , \psi _1 \land \psi _2$
, where
$\Gamma , \psi _1 \land \psi _2$
, where
![]() $\psi _1 \land \psi _2$
is the (necessarily
$\psi _1 \land \psi _2$
is the (necessarily
![]() $\Delta _0$
) principal formula of the inference used to derive
$\Delta _0$
) principal formula of the inference used to derive
![]() $C_j$
. Take the assignment
$C_j$
. Take the assignment
![]() $\alpha $
witnessing
$\alpha $
witnessing
![]() $\eta (s)$
at j, and let
$\eta (s)$
at j, and let
![]() $j' < j$
be such that
$j' < j$
be such that
![]() $C_j$
is
$C_j$
is
![]() $\Gamma , \psi _b$
for
$\Gamma , \psi _b$
for
![]() $b \in \{1,2\}$
such that
$b \in \{1,2\}$
such that
![]() $\alpha $
satisfies
$\alpha $
satisfies
![]() $\neg \psi _b$
. This
$\neg \psi _b$
. This
![]() $j'$
and the unchanged assignment
$j'$
and the unchanged assignment
![]() $\alpha $
witness
$\alpha $
witness
![]() $\eta (s+1)$
.
$\eta (s+1)$
.
If
![]() $C_j$
was derived by an
$C_j$
was derived by an
![]() $(\exists )$
inference, then
$(\exists )$
inference, then
![]() $C_j$
is
$C_j$
is
![]() $\Gamma , \exists w\, \psi $
and
$\Gamma , \exists w\, \psi $
and
![]() $C_{j'}$
is
$C_{j'}$
is
![]() $\Gamma , \psi (t)$
for some
$\Gamma , \psi (t)$
for some
![]() $j'<j$
. In this case, we first extend a given assignment
$j'<j$
. In this case, we first extend a given assignment
![]() $\alpha $
witnessing
$\alpha $
witnessing
![]() $\eta (s)$
at j to an assignment
$\eta (s)$
at j to an assignment
![]() $\alpha '$
by letting all variables that are free in
$\alpha '$
by letting all variables that are free in
![]() $C_{j'}$
but not in
$C_{j'}$
but not in
![]() $C_j$
have value
$C_j$
have value
![]() $0$
. If
$0$
. If
![]() $\psi (t)$
is not
$\psi (t)$
is not
![]() $\Pi _2$
(in which case
$\Pi _2$
(in which case
![]() $\neg \psi (t)$
is a
$\neg \psi (t)$
is a
![]() $\Pi _3$
but not
$\Pi _3$
but not
![]() $\Sigma _2$
subformula of one of the induction axioms
$\Sigma _2$
subformula of one of the induction axioms
![]() $\gamma _i$
) or
$\gamma _i$
) or
![]() $\exists w\,\psi $
is
$\exists w\,\psi $
is
![]() $\Sigma _1$
(in which case
$\Sigma _1$
(in which case
![]() $\forall w\, \neg \psi $
is
$\forall w\, \neg \psi $
is
![]() $\Pi _1$
and satisfied under
$\Pi _1$
and satisfied under
![]() $\alpha $
, so
$\alpha $
, so
![]() $\neg \psi (t)$
is satisfied under
$\neg \psi (t)$
is satisfied under
![]() $\alpha '$
), this is all we need to do in order to ensure that
$\alpha '$
), this is all we need to do in order to ensure that
![]() $j', \alpha '$
witness
$j', \alpha '$
witness
![]() $\eta (s+1)$
. The remaining case is when
$\eta (s+1)$
. The remaining case is when
![]() $\psi (t)$
is
$\psi (t)$
is
![]() $\Pi _2$
but
$\Pi _2$
but
![]() $\exists w\, \psi $
is not. In that situation,
$\exists w\, \psi $
is not. In that situation,
![]() $\neg \psi (t)$
arises from one of the
$\neg \psi (t)$
arises from one of the
![]() $\gamma _i$
’s by deleting the initial universal quantifier block and substituting some terms
$\gamma _i$
’s by deleting the initial universal quantifier block and substituting some terms
![]() $\bar t$
for the variables
$\bar t$
for the variables
![]() $\bar v$
appearing in that block. We know that
$\bar v$
appearing in that block. We know that
![]() $\alpha '$
satisfies
$\alpha '$
satisfies
![]() $\neg \psi (t)$
(because
$\neg \psi (t)$
(because
![]() $\gamma _i$
is true), but we also have to argue that we can witness the existential quantifiers
$\gamma _i$
is true), but we also have to argue that we can witness the existential quantifiers
![]() $\exists x \! < \! v_1 \,\exists \bar y$
in
$\exists x \! < \! v_1 \,\exists \bar y$
in
![]() $\neg \psi (t)$
by numbers below
$\neg \psi (t)$
by numbers below
![]() $d_{s+1}$
. However, we know that we can find a value for x below
$d_{s+1}$
. However, we know that we can find a value for x below
![]() $\alpha '(t_1)$
, which is the value of a term with at most m symbols on arguments below
$\alpha '(t_1)$
, which is the value of a term with at most m symbols on arguments below
![]() $d_s$
. Thus, by the definition of
$d_s$
. Thus, by the definition of
![]() $d_{s+1}$
, we can also find values for
$d_{s+1}$
, we can also find values for
![]() $\bar y$
corresponding to x in such a way that the maximum of these values is at most
$\bar y$
corresponding to x in such a way that the maximum of these values is at most
![]() $d_{s+1}$
.
$d_{s+1}$
.
Finally, if
![]() $C_j$
was derived by a
$C_j$
was derived by a
![]() $(\forall )$
inference, then
$(\forall )$
inference, then
![]() $C_j$
is
$C_j$
is
![]() $\Gamma , \forall w\, \psi $
and
$\Gamma , \forall w\, \psi $
and
![]() $C_{j'}$
is
$C_{j'}$
is
![]() $\Gamma , \psi (a)$
for some
$\Gamma , \psi (a)$
for some
![]() $j'<j$
and some variable a not appearing in
$j'<j$
and some variable a not appearing in
![]() $C_j$
. Let
$C_j$
. Let
![]() $\alpha $
be an assignment witnessing
$\alpha $
be an assignment witnessing
![]() $\eta (s)$
at j. There are two subcases to consider, depending on whether
$\eta (s)$
at j. There are two subcases to consider, depending on whether
![]() $\exists w\, \neg \psi $
is an unbounded
$\exists w\, \neg \psi $
is an unbounded
![]() $\Sigma _2$
formula or a
$\Sigma _2$
formula or a
![]() $\Delta _0$
formula. In the former case, we know from the inductive assumption that
$\Delta _0$
formula. In the former case, we know from the inductive assumption that
![]() $\alpha $
satisfies
$\alpha $
satisfies
![]() $\exists w\, \neg \psi $
and that there is a number
$\exists w\, \neg \psi $
and that there is a number
![]() $e \le d_s$
witnessing the quantifier
$e \le d_s$
witnessing the quantifier
![]() $\exists w$
. Then
$\exists w$
. Then
![]() $j'$
and the assignment
$j'$
and the assignment
![]() $\alpha \cup \{a:=e\}$
witness that
$\alpha \cup \{a:=e\}$
witness that
![]() $\eta (s+1)$
holds. In the latter case, we know that
$\eta (s+1)$
holds. In the latter case, we know that
![]() $\alpha $
satisfies
$\alpha $
satisfies
![]() $\exists w\, \neg \psi $
, and we also know that any number e witnessing the quantifier
$\exists w\, \neg \psi $
, and we also know that any number e witnessing the quantifier
![]() $\exists w$
must be bounded by the value of a term appearing in
$\exists w$
must be bounded by the value of a term appearing in
![]() $C_j$
(thus having at most m symbols) evaluated at elements of the range of
$C_j$
(thus having at most m symbols) evaluated at elements of the range of
![]() $\alpha $
, all of which are below
$\alpha $
, all of which are below
![]() $d_s$
. By definition of
$d_s$
. By definition of
![]() $d_{s+1}$
, this means that
$d_{s+1}$
, this means that
![]() $e \le d_{s+1}$
, so again
$e \le d_{s+1}$
, so again
![]() $j'$
and
$j'$
and
![]() $\alpha \cup \{a:=e\}$
witness that
$\alpha \cup \{a:=e\}$
witness that
![]() $\eta (s+1)$
holds.
$\eta (s+1)$
holds.
Acknowledgments
We are very grateful to Tin Lok Wong for many discussions and for making some observations that inspired the work presented in this paper. In fact, we felt that Wong’s contribution to the paper is such that he should be listed as a coauthor, but he does not feel that way himself. We are also grateful to Marta Fiori Carones for a thorough reading of the draft and number of useful comments. The first and second authors were partially supported by Grant No. 2017/27/B/ST1/01951 of the National Science Centre, Poland. The third author was partially supported by JSPS KAKENHI Grant No. 19K03601.