Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T18:04:25.791Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGH DIMENSIONAL ELLENTUCK SPACES AND INITIAL CHAINS IN THE TUKEY STRUCTURE OF NON-P-POINTS

Published online by Cambridge University Press:  09 March 2016

NATASHA DOBRINEN
NATASHA DOBRINEN*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF DENVER 2280 S VINE ST DENVER CO 80208, USAE-mail: [email protected]: http://web.cs.du.edu/∼ndobrine
Get access Rights & Permissions [Opens in a new window]

Abstract

The generic ultrafilter 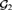${\cal G}_2 $ forced by 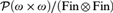${\cal P}\left( {\omega \times \omega } \right)/\left( {{\rm{Fin}} \otimes {\rm{Fin}}} \right)$ was recently proved to be neither maximum nor minimum in the Tukey order of ultrafilters ([1]), but it was left open where exactly in the Tukey order it lies. We prove 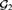${\cal G}_2 $ that is in fact Tukey minimal over its projected Ramsey ultrafilter. Furthermore, we prove that for each 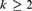${\cal G}_2 $, the collection of all nonprincipal ultrafilters Tukey reducible to the generic ultrafilter 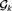${\cal G}_k $ forced by 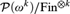${\cal P}\left( {\omega ^k } \right)/{\rm{Fin}}^{ \otimes k} $ forms a chain of length k. Essential to the proof is the extraction of a dense subset εk from (Fin⊗k)+ which we prove to be a topological Ramsey space. The spaces εk, k ≥ 2, form a hierarchy of high dimensional Ellentuck spaces. New Ramsey-classification theorems for equivalence relations on fronts on εk are proved, extending the Pudlák–Rödl Theorem for fronts on the Ellentuck space, which are applied to find the Tukey and Rudin–Keisler structures below 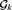${\cal G}_k $.

Keywords

03E0503E0205D10Ellentuck spaceultrafilterTukey typeRamsey theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 1 , March 2016 , pp. 237 - 263
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Blass, Andreas, Dobrinen, Natasha, and Raghavan, Dilip, The next best thing to a p-point, this Journal, vol. 80 (2015), no. 3, pp. 866–900.Google Scholar
Carlson, Timothy J. and Simpson, Stephen G., Topological Ramsey theory, Mathematics of Ramsey Theory, Algorithms and Combinatorics, vol. 5, Springer, 1990, pp. 172–183.Google Scholar
Di Prisco, Carlos, Mijares, José Grigorio, and Nieto, Jesús, Local Ramsey theory. An abstract approach, 2014, 16 p., submitted.Google Scholar
Dobrinen, Natasha, Survey on the Tukey theory of ultrafilters, Selected Topics in Combinatorial Analysis, Zbornik Radova, Mathematical Institutes of the Serbian Academy of Sciences, vol. 17 (2015), no. 5, pp. 53–80.Google Scholar
Dobrinen, Natasha, Grigorio Mijares, José, and Trujillo, Timothy, Topological Ramsey spaces from Fraïssé classes, Ramsey-classification theorems, and initial structures in the Tukey types of p-points, Archive for Mathematical Logic, 35 p., to appear.Google Scholar
Dobrinen, Natasha and Todorcevic, Stevo, Tukey types of ultrafilters. Illinois Journal of Mathematics, vol. 55 (2011), no. 3, pp. 907–951.Google Scholar
Dobrinen, Natasha and Todorcevic, Stevo, A new class of Ramsey-classification Theorems and their applications in the Tukey theory of ultrafilters, Part 1. Transactions of the American Mathematical Society, vol. 366 (2014), no. 3, pp. 1659–1684.Google Scholar
Dobrinen, Natasha and Todorcevic, Stevo, A new class of Ramsey-classification Theorems and their applications in the Tukey theory of ultrafilters, Part 2. Transactions of the American Mathematical Society, vol. 367 (2015), no. 7, 4627–4659.Google Scholar
Ellentuck, Erik, A new proof that analytic sets are Ramsey, this Journal, vol. 39 (1974), no. 1, pp. 163–165.Google Scholar
Erdős, Paul and Rado, Richard, A combinatorial theorem. Journal of the London Mathematical Society, vol. 25 (1950), pp. 249–255.Google Scholar
Isbell, John, The category of cofinal types. II. Transactions of the American Mathematical Society, vol. 116 (1965), pp. 394–416.Google Scholar
Milovich, David, Tukey classes of ultrafilters on ω. Topology Proceedings, vol. 32 (2008), pp. 351–362.Google Scholar
Pudlák, Pavel and Rödl, Vojtech, Partition theorems for systems of finite subsets of integers. Discrete Mathematics, vol. 39 (1982), pp. 67–73.Google Scholar
Raghavan, Dilip and Todorčević, Stevo, Cofinal types of ultrafilters. Annals of Pure and Applied Logic, vol. 163 (2012), no. 3, pp. 185–199.Google Scholar
Todorčević, Stevo, Introduction to Ramsey Spaces, Princeton University Press, Princeton, 2010.Google Scholar