Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T11:32:28.967Z Has data issue: false hasContentIssue false
  • English
  • Français

Gödel sentences of bounded arithmetic

Published online by Cambridge University Press:  12 March 2014

Gaisi Takeuti
Gaisi Takeuti*
Affiliation:
1420 Locust Street 35R, Philadelphia, PA 19102, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In [1], S. Buss introduced the systems of Bounded Arithmetic for (i = 0,1,2,…) which has a close relationship to classes in polynomial hierarchy.

In [4], we defined a very special kind of proof-predicate Prfi for which gives detailed information on bounds of free variables used in the proof. There we also introduced infinitely many Gödel sentences 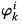for Prfi (k = 0, 1, 2, …) and showed that the properties of Prfi and 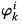are closely related to the P ≠ NP problem. Then we presented many conjectures on Prfi and 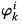which imply P ≠ NP.

Now in [2], Feferman emphasized that the arithmetization of metamathematics must be carried out intensionally. Bounded Arithmetic is a very interesting case in this sense.

In this paper, we also introduce the usual proof-predicate PRFi for and infinitely many Gödel sentences 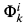for PRFi(k= 0, 1, 2, …). Then we show that (Prfi, 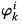)and (PRFi, 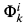) form a good contrast, this contrast is also closely related to the P ≠ NP problem, and present more conjectures which imply P ≠ NP.

As in [4] we define to be the following extension of Buss' original .

(1) We add finitely many function symbols which express polynomial time computable functions to Buss' original language of .

(2) All basic axioms on function symbols and ≤ can be expressed by initial sequents without logical symbols.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 3 , September 2000 , pp. 1338 - 1346
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buss, S., Bounded arithmetic, Bibliopolis, Napoli, 1986.Google Scholar
[2]Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
[3]Takeuti, G., Bounded arithmetic and truth definition, Annals of Pure and Applied Logic, vol. 39 (1988), pp. 75–104.CrossRefGoogle Scholar
[4]Takeuti, G., Incompleteness theorems and versus , Logic Colloquium '96 (Larrazabal, J. M., Lascar, D., and Mints, G., editors), LN in Logic, no. 12, Springer, 1998, pp. 247–261.Google Scholar
[5]Wilkie, A. J. and Paris, J. B., On the scheme of induction for bounded arithmetic formulas, Annals of Pure and Applied Logic, vol. 35 (1987), pp. 261–302.CrossRefGoogle Scholar