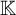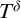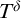Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
FORNASIERO, ANTONGIULIO
and
TERZO, GIUSEPPINA
2024.
GENERIC DERIVATIONS ON ALGEBRAICALLY BOUNDED STRUCTURES.
The Journal of Symbolic Logic,
p.
1.