Published online by Cambridge University Press: 12 March 2014
An effective translation of the fact that any infinite ordered set contains an infinite ascending or descending sequence is that any infinite recursive set A ⊆ Q has a recursive subset with order type ω or ω*. Tennenbaum's theorem states that this translation is false, and there is a counterexample A with order type ω + ω*. Tennenbaum suggested that this counterexample is an infinite recursive linearly ordered set which is effectively finite, and that the collection of all such counterexamples could provide a concrete model of nonstandard arithmetic. The purpose of this paper is to determine the collection of order types for which there is a counterexample.
It is readily seen that any counterexample to the effective translation must have order type ω + Z · α + ω* for some α [2], [3]. Let 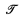 be the collection of order types α for which there is a counterexample. As a test case, we have previously shown that
be the collection of order types α for which there is a counterexample. As a test case, we have previously shown that 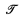 contains the constructive scattered orderings [3], [4]. In this paper we determine exactly which order types are in
contains the constructive scattered orderings [3], [4]. In this paper we determine exactly which order types are in 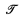 . We easily show that if ω+ Z · α + ω* is recursive, then α is
. We easily show that if ω+ Z · α + ω* is recursive, then α is 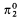 . The main result is that
. The main result is that 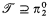 . Consequently,
. Consequently, 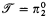 .
.