No CrossRef data available.
Article contents
Generalised weak presentations
Published online by Cambridge University Press: 12 March 2014
Abstract
Let K be a computable field. Let ℱ be a collection of recursive functions over K, possibly including field operations. We investigate the following question. Given an r.e. degree 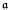 . is there an injective map j : K → ℕ such that j(K) is of degree a and all the functions in ℱ are translated by restrictions of total recursive functions.
. is there an injective map j : K → ℕ such that j(K) is of degree a and all the functions in ℱ are translated by restrictions of total recursive functions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
[1]Artin, E., Algebraic Numbers and Algebraic Functions, Gordon Breach Science Publishers, New York, 1986.Google Scholar
[2]Ash, C. J. and Knight, J. F., Possible degrees in recursive copies, Annals of Pure and Applied Logic, vol. 75 (1995), no. 3, pp. 215–221.CrossRefGoogle Scholar
[3]Ash, C. J., Possible degrees in rucursive copies, II, Annals of Pure and Applied Logic, vol. 87 (1997), no. 2, pp. 151–165.CrossRefGoogle Scholar
[4]Ash, C. J., Knight, J. F., and Remmel, J. B., Quasi-simple relations in copies of a given recursive structure, Annals of Pure and Applied Logic, vol. 86, no. 3, pp. 203–218.CrossRefGoogle Scholar
[5]Baker, A., Transcendental Number Theory, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1990.Google Scholar
[6]Chevalley, C., Introduction to the theory of algebraic functions of one variable, Mathematical Surveys, vol. 6, AMS, Providence, RI, 1951.CrossRefGoogle Scholar
[7]Fried, M. and Jarden, M., Field Arithmetic, Springer Verlag, New York, 1986.CrossRefGoogle Scholar
[8]Harizanov, V., Some effects of Ash-Nerode and other decidability conditions on degree spectra, Annals of Pure and Applied Logic, vol. 55 (1991), pp. 51–65.CrossRefGoogle Scholar
[9]Harizanov, V., Uncountable degree spectra, Annals of Pure and Applied Logic, vol. 54 (1991), pp. 255–263.CrossRefGoogle Scholar
[10]Harizanov, V., The possible Turing degree of the nonzero member in a two element degree spectrum, Annals of Pure and Applied Logic, vol. 60 (1993), pp. 1–30.CrossRefGoogle Scholar
[12]Jockusch, C. and Shlapentokh, A., Weak presentations of computable fields, this Journal, vol. 60 (1995), pp. 199–208.Google Scholar
[13]Rabin, M., Computable algebra, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[14]Shlapentokh, A., Diophantine equivalence and countable rings, this Journal, vol. 59 (1994), pp. 1068–1095.Google Scholar
[15]Shlapentokh, A., Non-standard extensions of weak presentations, Journal of Algebra, vol. 176 (1995), pp. 735–749.CrossRefGoogle Scholar
[16]Shlapentokh, A., Algebraic and Turing separability of rings, Journal of Algebra, vol. 185 (1996), pp. 229–257.CrossRefGoogle Scholar
[17]Shlapentokh, A., Rational separability over global fields, Annals of Pure and Applied Logic, vol. 79 (1996), pp. 93–108.CrossRefGoogle Scholar
[18]Shlapentokh, A., The logic ofpseudo S-integers, Israel Journal of Mathematics, vol. 101 (1997), pp. 229–254.CrossRefGoogle Scholar
[19]Shlapentokh, A., Weak presentations of fields not extendible to recursive presentations, Recursion Theory and Complexity, Proceedings of the International Workshop on Complexity and Computability, 1997, pp. 131–155.Google Scholar
[20]Shlapentokh, A., Weak presentations of non-finitely generated fields, Annals of Pure and Applied Logic, vol. 28 (1998), pp. 223–252.CrossRefGoogle Scholar


