No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
In the past 10 years much progress occurred in the direction of unifying the treatment of finitary Lωω and infinitary  logic. We have especially in mind the study of countable admissible fragments (of which Lωω is a particular case) initiated by Barwise in [1] (cf. also [2]), the introduction of
logic. We have especially in mind the study of countable admissible fragments (of which Lωω is a particular case) initiated by Barwise in [1] (cf. also [2]), the introduction of  -recursively saturated structures by Ressayre in [22] (for
-recursively saturated structures by Ressayre in [22] (for 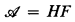 these were independently introduced in [3]) and game sentences as studied by Vaught in [26] (see also Svenonius [25] and Moschovakis [19], [20]). A good reference for these topics is [17].
these were independently introduced in [3]) and game sentences as studied by Vaught in [26] (see also Svenonius [25] and Moschovakis [19], [20]). A good reference for these topics is [17].
In this paper we illustrate the use of these tools for deducing definability theorems. We go beyond the known results as seen from the discussion that follows.
Let L be a language and P a (say, unary) additional predicate. Consider a sentence σ(P) in the language L(P). There are two types of definability theorems: the “Beth type” and the “Svenonius type”. Beth's theorem [4] characterizes the condition:
(i)′ for any 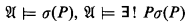 ;
;
while Svenonius' result [24] characterizes:
(i)″ for any 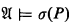 , every L-automorphism of
, every L-automorphism of 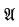 is an L(P)-automorphism.
is an L(P)-automorphism.