Published online by Cambridge University Press: 12 March 2014
This paper is the sequel of “a functorial construction of the Veblen hierarchy” [GV]: it was announced in it.
We define the notion of garden (Definition I.1.6), that is a functorial version of a Bachmann collection: in a garden Jy, at each ordinal x ≤ y, of cofinality Ω, is associated an Ω-flower (Definition I.1.1); we define also the notion of a function compatible with a garden (Definition I.3.3). We construct a hierarchy 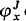 of functors from Ω to Ω (for each x ≤ y and x ∈ Jy) and for each function (f ∈ I(x, y) compatible with Jy a natural transformation T(f) from
of functors from Ω to Ω (for each x ≤ y and x ∈ Jy) and for each function (f ∈ I(x, y) compatible with Jy a natural transformation T(f) from 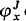 to
to 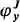 ; we show that, if the garden is Gε Ω + 1 (Definition I.2.1), then, for each ordinal x ≤ εΩ + 1, the hierarchy of functions
; we show that, if the garden is Gε Ω + 1 (Definition I.2.1), then, for each ordinal x ≤ εΩ + 1, the hierarchy of functions 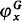 coincides exactly with the usual hierarchy ψx constructed using the usual Bachmann collection of height εΩ + 1, and founded on composition (that is, ψx + 1 = ψx ˚ ψ1; then,
coincides exactly with the usual hierarchy ψx constructed using the usual Bachmann collection of height εΩ + 1, and founded on composition (that is, ψx + 1 = ψx ˚ ψ1; then, 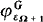 (0) is the usual Howard ordinal. We show also, that for eac x ≤ y, φx is an Ω-flower, and so we can use this hierarchy of functors for ordinal notations: see Chapter II of
(0) is the usual Howard ordinal. We show also, that for eac x ≤ y, φx is an Ω-flower, and so we can use this hierarchy of functors for ordinal notations: see Chapter II of  -logic [G].
-logic [G].
The construction made in this article corresponds, essentially, to Chapter V of  -logic [G]: the exact connections between these two works will be the matter of a subsequent article.
-logic [G]: the exact connections between these two works will be the matter of a subsequent article.