Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T05:41:50.606Z Has data issue: false hasContentIssue false
  • English
  • Français

A form of feasible interpolation for constant depth Frege systems

Published online by Cambridge University Press:  12 March 2014

Jan Krajíček
Jan Krajíček*
Affiliation:
Charles University, Faculty of Mathematics and Physics Department of Algebra Sokolovská 83, Prague 8, Cz-186 75, Czech Republic. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let L be a first-order language and Φ and Ψ two 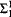L-sentences that cannot be satisfied simultaneously in any finite L-structure. Then obviously the following principle ChainL,Φ,Ψ(n, m) holds: For any chain of finite L-structures C1, …, Cm with the universe [n] one of the following conditions must fail:

For each fixed L and parameters n, m the principle ChainL,Φ,Ψ(n,m) can be encoded into a propositional DNF formula of size polynomial in n, m.

For any language L containing only constants and unary predicates we show that there is a constant CL such that the following holds: If a constant depth Frege system in DeMorgan language proves ChainL,Φ,Ψ(n, cL . n) by a size s proof then the class of finite L-structures with universe [n] satisfying Φ can be separated from the class of those L-structures on [n] satisfying ψ by a depth 3 formula of size 2log(S)O(1) and with bottom fan-in log(S)O(1).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 2 , June 2010 , pp. 774 - 784
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ajtai, M., The complexity of the pigeonhole principle. Proceedings of the IEEE Annual Symposium on Foundations of Computer Science (FOCS), 1988, pp. 346–355.Google Scholar
[2]Bonet, M. L., Domingo, C., Gavalda, R., Maciel, A., and Pitassi, T., Non-automatizability of bounded-depth Frege proofs, Computational Complexity, vol. 13 (2004), pp. 47–68.CrossRefGoogle Scholar
[3]Bonet, M. L., Pitassi, T., and Raz, R., Lower bounds for cutting planes proofs with small coefficients, this Journal, (1997), pp. 708–728.Google Scholar
[4]Bonet, M. L., On interpolation and automatization for Frege systems, SIAM Journal on Computing, vol. 29 (2000), no. 6, pp. 1939–1967.CrossRefGoogle Scholar
[5]Buss, S. R., Bounded Arithmetic, Naples, Bibliopolis, 1986.Google Scholar
[6]Buss, S. R., The prepositional pigeonhole principle has polynomial size Frege proofs, this Journal, vol. 52 (1987), pp. 916–927.Google Scholar
[7]Cook, S. A. and Nguyen, P., Logical foundations of proof complexity, Perspectives in Logic, Cambridge University Press, 2010.CrossRefGoogle Scholar
[8]Cook, S. A. and Reckhow, A. R., The relative efficiency of prepositional proof systems, this Journal, vol. 44 (1979), no. 1, pp. 36–50.Google Scholar
[9]Hastad, J., Almost optimal lower bounds for small depth circuits, Randomness and Computation (Micali, S., editor), Advances in Computing Research, vol. 5, JAI Press, 1989, pp. 143–170.Google Scholar
[10]Krajíček, J., Lower bounds to the size of constant-depth prepositional proofs, this Journal, vol. 59 (1994), no. 1, pp. 73–86.Google Scholar
[11]Krajíček, J., Bounded arithmetic, prepositional logic, and complexity theory, Encyclopedia of Mathematics and Its Applications, vol. 60, Cambridge University Press, 1995.CrossRefGoogle Scholar
[12]Krajíček, J., Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic, this Journal, vol. 62 (1997), no. 2, pp. 457–486.Google Scholar
[13]Krajíček, J., Discretely ordered modules as a first-order extension of the cutting planes proof system, this Journal, vol. 63 (1998), no. 4, pp. 1582–1596.Google Scholar
[14]Krajíček, J., An exponential lower bound for a constraint propagation proof system based on ordered binary decision diagrams, this Journal, vol. 73 (2008), no. 1, pp. 227–237.Google Scholar
[15]Krajíček, J. and Pudlák, P., Some consequences of cryptographical conjectures for and EF, Logic and Computational Complexity (Proceedings of the Meeting held in Indianapolis, October 1994) (Leivant, D., editor), Lecture Notes in Computer Science, vol. 960, Springer-Verlag, 1995, Revised version in: Information and Computation, 140 (1998), no. 1, pp. 82–94, pp. 210–220.Google Scholar
[16]Krajíček, J., P. Pudlák, and Woods, A., An exponential lower bound to the size of bounded depth Frege proofs of the pigeonhole, Random Structures and Algorithms, vol. 7 (1995), no. 1, pp. 15–39.CrossRefGoogle Scholar
[17]Paris, J. B. and Wilkie, A. J., Counting problems in bounded arithmetic, Methods in Mathematical Logic, Lecture Notes in Mathematics, vol. 1130, Springer-Verlag, 1985, pp. 317–340.CrossRefGoogle Scholar
[18]Paris, J. B., Wilkie, A. J., and Woods, A. R., Provability of the pigeonhole principle and the existence of infinitely many primes, this Journal, vol. 53 (1988), pp. 1235–1244.Google Scholar
[19]Pitassi, T., Beame, P., and Impagliazzo, R., Exponential lower bounds for the pigeonhole principle, Computational Complexity, vol. 3 (1993), pp. 97–308.CrossRefGoogle Scholar
[20]Pudlák, P., Lower bounds for resolution and cutting plane proofs and monotone computations, this Journal, (1997), pp. 981–998.Google Scholar
[21]Pudlák, P., The lengths of proofs, Handbook of Proof Theory (Buss, S. R., editor), Elsevier, 1998, pp. 547–637.CrossRefGoogle Scholar
[22]Pudlák, P. and Sgall, J., Algebraic models of computation and interpolation for algebraic proof systems, Proof Complexity and Feasible Arithmetic (Beame, P. and Buss, S. R., editors), DIMACS Series in Discrete Mathematics and Computer Science, vol. 39, American Mathematical Society, 1998, pp. 179–205.Google Scholar
[23]Razborov, A. A., Unprovability of lower bounds on the circuit size in certain fragments of bounded arithmetic, Izvestiya: Mathematics, vol. 59 (1995), no. 1, pp. 205–227.CrossRefGoogle Scholar
[24]Skelley, A. and Thapen, N., The provably total search problems of bounded arithmetic, 2008, Submitted.Google Scholar
[25]Yao, A., Separating the polynomial-time hierarchy by oracles, Proceedings of the IEEE Annual Symposium on Foundations of Computer Science (FOCS), 1985, pp. 1–10.Google Scholar