Article contents
FORKING, IMAGINARIES, AND OTHER FEATURES OF 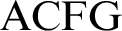 $\text {ACFG}$
$\text {ACFG}$
Published online by Cambridge University Press: 07 June 2021
Abstract
We study the generic theory of algebraically closed fields of fixed positive characteristic with a predicate for an additive subgroup, called 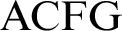 $\mathrm {ACFG}$
. This theory was introduced in [16] as a new example of
$\mathrm {ACFG}$
. This theory was introduced in [16] as a new example of 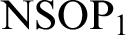 $\mathrm {NSOP}_{1}$
nonsimple theory. In this paper we describe more features of
$\mathrm {NSOP}_{1}$
nonsimple theory. In this paper we describe more features of 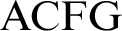 $\mathrm {ACFG}$
, such as imaginaries. We also study various independence relations in
$\mathrm {ACFG}$
, such as imaginaries. We also study various independence relations in  $\mathrm {ACFG}$
, such as Kim-independence or forking independence, and describe interactions between them.
$\mathrm {ACFG}$
, such as Kim-independence or forking independence, and describe interactions between them.
Keywords
- Type
- Article
- Information
- Copyright
- © The Association for Symbolic Logic 2021
References
REFERENCES
- 6
- Cited by



