No CrossRef data available.
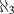 $\aleph _3 $ AND PRESERVING ALL OTHER CARDINALS
$\aleph _3 $ AND PRESERVING ALL OTHER CARDINALSPublished online by Cambridge University Press: 21 December 2018
I construct, in ZFC, a forcing notion that collapses 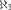 $\aleph _3 $ and preserves all other cardinals. The existence of such a forcing answers a question of Uri Abraham from 1983.
$\aleph _3 $ and preserves all other cardinals. The existence of such a forcing answers a question of Uri Abraham from 1983.