Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T23:04:06.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Forcing isomorphism

Published online by Cambridge University Press:  12 March 2014

J. T. Baldwin ,
M. C. Laskowski  and
S. Shelah
J. T. Baldwin
Affiliation:
Department of Mathematics, University of Illinois, Chicago, Illinois 60680, E-mail: U128O0@UICVM
M. C. Laskowski
Affiliation:
Department of Mathematics, University of Maryland, College Park, Maryland 20742, E-mail: [email protected]
S. Shelah
Affiliation:
Department of Mathematics, Hebrew University of Jerusalem, Jerusalem, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

If two models of a first-order theory are isomorphic, then they remain isomorphic in any forcing extension of the universe of sets. In general however, such a forcing extension may create new isomorphisms. For example, any forcing that collapses cardinals may easily make formerly nonisomorphic models isomorphic. However, if we place restrictions on the partially-ordered set to ensure that the forcing extension preserves certain invariants, then the ability to force nonisomorphic models of some theory T to be isomorphic implies that the invariants are not sufficient to characterize the models of T.

A countable first-order theory is said to be classifiable if it is superstable and does not have either the dimensional order property (DOP) or the omitting types order property (OTOP). If T is not classifiable, Shelah has shown in [5] that sentences in L∞,λ do not characterize models of T of power λ. By contrast, in [8] Shelah showed that if a theory T is classifiable, then each model of cardinality λ is described by a sentence of L∞,λ. In fact, this sentence can be chosen in the 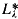. ( 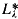is the result of enriching the language 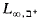by adding for each μ < λ a quantifier saying the dimension of a dependence structure is greater than μ) Further work ([3], [2]) shows that ⊐+ can be replaced by ℵ1.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1291 - 1301
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T., Diverse classes, this Journal, vol. 54 (1989), pp. 875–893.Google Scholar
[2]Buechler, Steve and Shelah, Saharon, On the existence of regular types, Annals of Pure and Applied Logic, vol. 45 (1989), pp. 207–308.Google Scholar
[3]Hart, Bradd, Some results in classification theory, Ph.D. Thesis, McGill University, Montreal, 1986.Google Scholar
[4]Shelah, S., Classification theory and the number of nonisomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[5]Shelah, S., Classification of first-order theories which have a structure theory, Bulletin of the American Mathematical Society, vol. 12 (1985), pp. 227–232.CrossRefGoogle Scholar
[6]Shelah, S., Existence of many L∞,λ-equivalent nonisomorphic models of T of power λ, Annals of Pure and Applied Logic, vol. 34 (1987).CrossRefGoogle Scholar
[7]Shelah, S., Universal classes: Part 1, Classification Theory, Chicago 1985 (Baldwin, J., editor), Lecture Notes in Mathematics, vol. 1292, Springer-Verlag, Berlin and New York, 1987, pp. 264–419.Google Scholar
[8]Shelah, S., Classification theory, North-Holland, Amsterdam, 1991 (second edition of [4]).Google Scholar
[9]Weiss, W., Versions of Martin's axiom, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984.Google Scholar