Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-25T13:44:26.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Finitely generated free Heyting algebras: the well-founded initial segment

Published online by Cambridge University Press:  12 March 2014

R. Elageili  and
J. K. Truss
R. Elageili
Affiliation:
Department of Mathematics, University of Garyounis ‘Benghazi’, Benghazi, Libya, E-mail: [email protected]
J. K. Truss
Affiliation:
Department of Mathematics, University of Garyounis ‘Benghazi’, Benghazi, Libya, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we describe the well-founded initial segment of the free Heyting algebra 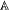α on finitely many, α, generators. We give a complete classification of initial sublattices of 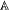2 isomorphic to 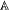1 (called ‘low ladders’), and prove that for 2 ≤ α < ω, the height of the well-founded initial segment of 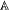α is ω2.

Keywords

free Heyting algebrawell-foundedlow ladder
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 4 , December 2012 , pp. 1291 - 1307
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Bellissima, F., Finitely generated free Heyting algebras, this Journal, vol. 51 (1986), pp. 152–165.Google Scholar
[2]Darnière, L. and Junker, M., On Belissima's construction of the finitely generated free Heyting algebras and beyond. Archive for Mathematical Logic, vol. 49 (2010), pp. 743–771.CrossRefGoogle Scholar
[3]Elageili, R., Free Heyting algebras, Ph.D. thesis, University of Leeds, 2011.Google Scholar
[4]Grigolia, R., Free and projective Heyting and monadic Heyting algebras, Non-classical logics and their applications to fuzzy subsets (Höhle, U. and Klement, E. P., editors), Kluwer, 1995, pp. 33–52.CrossRefGoogle Scholar
[5]Johnstone, P. T., Stone spaces, Cambridge University Press, 1982.Google Scholar
[6]Kleene, S. C, Introduction to metamathematics, North-Holland, 1964.Google Scholar
[7]Nishimura, I., On formulas in one variable in intuitionistic propositional calculus, this Journal, vol. 25 (1960), pp. 327–331.Google Scholar
[8]Riger, L., Zametki o t. naz. svobodnyh algebrah c zamykaniami, Czechoslovak Mathematical Journal, vol. 7 (1957), no. 82, pp. 16–20.Google Scholar
[9]Troelstra, A. S. and van Dalen, D., Constructivism in mathematics, North-Holland, 1988.Google Scholar
[10]Urquhart, A., Free Heyting algebras, Algebra Universalis, vol. 3 (1973), pp. 94–97.CrossRefGoogle Scholar