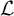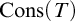1. Introduction
The author was motivated to consider this topic by the following question:
Problem 1.1. Does there exist an infinite, finitely axiomatisable field?
This (still open) problem was posed explicitly by I. Kaplan at the 2016 Oberwolfach workshop on Definability and Decidability Problems in Number Theory [Reference Koenigsmann, Pasten, Shlapentokh and Vidaux33, Q4], though existed as folklore before. This relates closely to another elementary question:
Problem 1.2. Does there exist a finitely axiomatisable theory of fields which is decidable and has an infinite model?
That is, this problem is to ascertain the existence of an infinite field F and a collection of first-order sentences T in the language of rings
![]() $\mathcal {L}_r$
, such that
$\mathcal {L}_r$
, such that
![]() $T \subseteq {\mathtt{Th}}(F; \mathcal {L}_r)$
, T is finitely axiomatised, T models the field axioms, and there exists a decision procedure to determine membership of
$T \subseteq {\mathtt{Th}}(F; \mathcal {L}_r)$
, T is finitely axiomatised, T models the field axioms, and there exists a decision procedure to determine membership of
![]() $\mbox {Cons}(T)$
—the set of
$\mbox {Cons}(T)$
—the set of
![]() $\mathcal {L}_r$
-sentences
$\mathcal {L}_r$
-sentences
![]() $\phi $
such that
$\phi $
such that
![]() $T \models \phi $
.
$T \models \phi $
.
Answering Problem 1.2
in the negative (as the empirical evidence suggests might indeed be the case) would answer Problem 1.1
in the negative too. This is the focus of modern investigations. One approach to this was established by Ziegler [Reference Ziegler49], and generalised further by Shlapentokh and Videla [Reference Shlapentokh and Videla43]. Ziegler’s idea was to take a finitely axiomatised subtheory of a sufficiently saturated field with a powerful model completeness property (he considered
![]() $\operatorname {\mathbb {C}}$
,
$\operatorname {\mathbb {C}}$
,
![]() $\widetilde {\mathbb {F}_p(t)}$
—where “
$\widetilde {\mathbb {F}_p(t)}$
—where “
![]() $\,\widetilde {F}\,$
” denotes the algebraic closure of a field F—
$\,\widetilde {F}\,$
” denotes the algebraic closure of a field F—
![]() $\operatorname {\mathbb {R}}$
, and
$\operatorname {\mathbb {R}}$
, and
![]() $\operatorname {\mathbb {Q}}_p$
) and prove it to be a subtheory of a field interpreting arithmetic. By using a result of Tarski (see below), there is no nonempty finitely axiomatised subtheory (“finite subtheory”) of ACF
$\operatorname {\mathbb {Q}}_p$
) and prove it to be a subtheory of a field interpreting arithmetic. By using a result of Tarski (see below), there is no nonempty finitely axiomatised subtheory (“finite subtheory”) of ACF
![]() ${}_0$
, ACF
${}_0$
, ACF
![]() ${}_p$
, RCF, or p
CF that is decidable. With this in mind we forward the following definitionFootnote
1
:
${}_p$
, RCF, or p
CF that is decidable. With this in mind we forward the following definitionFootnote
1
:
Definition 1.3. A theory T in a language
![]() $\mathcal {L}$
is finitely undecidable if every finitely axiomatised
$\mathcal {L}$
is finitely undecidable if every finitely axiomatised
![]() $\mathcal {L}$
-subtheory of T is undecidable. (An
$\mathcal {L}$
-subtheory of T is undecidable. (An
![]() $\mathcal {L}$
-structure is finitely undecidable if its complete
$\mathcal {L}$
-structure is finitely undecidable if its complete
![]() $\mathcal {L}$
-theory is.)
$\mathcal {L}$
-theory is.)
What infinite fields are finitely undecidable (implicitly: in
![]() $\mathcal {L}_r$
)? That is the motivating question for this paper and its sequel. If there exists a field satisfying Problem 1.1
or
1.2
, this field is not finitely undecidable; we will show, however, there is a considerably broad class of fields whose members have this undecidability property.
$\mathcal {L}_r$
)? That is the motivating question for this paper and its sequel. If there exists a field satisfying Problem 1.1
or
1.2
, this field is not finitely undecidable; we will show, however, there is a considerably broad class of fields whose members have this undecidability property.
In particular, most (if not all) infinite fields whose model theory in the language of rings is well understood will be finitely undecidable, as we will argue. Following this philosophy, we are motivated by a long-standing model theory conjecture:
Conjecture (Shelah’s NIP Fields Conjecture)
Every infinite NIP field is either separably closed, real closed, or admits a nontrivial henselian valuation.
In [Reference Tyrrell47] we consider other classification-theoretic conjectures on field theories. Here, we adapt Ziegler’s argument to SCF
![]() ${}_{p, e}$
(Section 3) and the complete theories of certain henselian valued fields in the language
${}_{p, e}$
(Section 3) and the complete theories of certain henselian valued fields in the language
![]() $\mathcal {L}_{val}$
; the language of rings with an additional unary predicate for the valuation ring (Sections 4 and 5). Our main result is:
$\mathcal {L}_{val}$
; the language of rings with an additional unary predicate for the valuation ring (Sections 4 and 5). Our main result is:
Theorem (Corollary 4.10 + Theorem 5.3 + Theorem 5.8)
Let
![]() $(K, v)$
be an
$(K, v)$
be an
-
• equicharacteristic
 $0$
, or
$0$
, or -
• mixed characteristic, or
-
• equicharacteristic
 $p>0$
separably defectless Kaplansky
$p>0$
separably defectless Kaplansky
henselian nontrivially valued field. Then
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
![]() $\mathcal {O}_v$
is
$\mathcal {O}_v$
is
![]() $\mathcal {L}_r$
-definable, K is finitely undecidable as a field.
$\mathcal {L}_r$
-definable, K is finitely undecidable as a field.
Thanks to some deeper results in classification theory, some immediate consequences of this are:
Corollary 5.9.
-
(1) If
 $(K, v)$
is an NIP henselian nontrivially valued field,
$(K, v)$
is an NIP henselian nontrivially valued field,
 ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable. Furthermore if
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable. Furthermore if
 $\mathcal {O}_v$
is
$\mathcal {O}_v$
is
 $\mathcal {L}_r$
-definable in K, then K is finitely undecidable as a field.
$\mathcal {L}_r$
-definable in K, then K is finitely undecidable as a field. -
(2) Every infinite dp-finite field is finitely undecidable.
-
(3) Assuming the NIP Fields Conjecture, every infinite NIP field is finitely undecidable.
We recall the notion of a dp-finite field L below (for a full, general discussion of dp-rank, see [Reference Kaplan, Onshuus and Usvyatsov31, Reference Simon45]). We work in a sufficiently saturated model of
![]() ${\mathtt{Th}}(L; \mathcal {L}_r)$
.
${\mathtt{Th}}(L; \mathcal {L}_r)$
.
Definition 1.4. For
![]() $n \in \operatorname {\mathbb {N}}_{>0}$
, let
$n \in \operatorname {\mathbb {N}}_{>0}$
, let
![]() $I_1, \dots , I_n$
be a list of sequences, and A a set of parameters. We say that the sequences
$I_1, \dots , I_n$
be a list of sequences, and A a set of parameters. We say that the sequences
![]() $I_1, \dots , I_n$
are mutually indiscernible over A if for each
$I_1, \dots , I_n$
are mutually indiscernible over A if for each
![]() $1 \leq t \leq n$
, the sequence
$1 \leq t \leq n$
, the sequence
![]() $I_t$
is indiscernible over
$I_t$
is indiscernible over
![]() $A \cup I_{\neq t}$
.
$A \cup I_{\neq t}$
.
If p is a partial type over A, we say p is of dp-rank
![]() $\geq n$
if there exist
$\geq n$
if there exist
![]() $a \models p$
and a list of sequences
$a \models p$
and a list of sequences
![]() $I_1, \dots , I_n$
mutually indiscernible over A such that
$I_1, \dots , I_n$
mutually indiscernible over A such that
![]() $I_k$
is not indiscernible over
$I_k$
is not indiscernible over
![]() $A \cup \{a\}$
for
$A \cup \{a\}$
for
![]() $1 \leq k \leq n$
. (The dp-rank of a partial type is always
$1 \leq k \leq n$
. (The dp-rank of a partial type is always
![]() $\geq 0$
.)
$\geq 0$
.)
This definition does not in fact depend on the parameter set A, as evidenced by Simon [Reference Simon45, Lemma 4.14].
Definition 1.5. A field L is of finite dp-rank if for some
![]() $m \in \operatorname {\mathbb {N}}$
, “
$m \in \operatorname {\mathbb {N}}$
, “
![]() $x = x$
” has dp-rank
$x = x$
” has dp-rank
![]() $\geq \ m$
but does not have dp-rank
$\geq \ m$
but does not have dp-rank
![]() $\geq \ m+1$
.
$\geq \ m+1$
.
See Example 5.10
for “interesting” examples of Theorem (Corollary 4.10
![]() $+$
Theorem 5.3
$+$
Theorem 5.3
![]() $+$
Theorem 5.8
) and Corollary 5.9
in action.
$+$
Theorem 5.8
) and Corollary 5.9
in action.
All of our undecidability results rely on a theorem of Tarksi, which we now state: general references for this material are [Reference Ershov, Lavrov, Taimanov and Taitslin15, Reference Shoenfield44, Reference Tarski, Mostowski and Robinson46].
Theorem 1.6 (Tarski)
Let
![]() $\mathcal {L}_1$
,
$\mathcal {L}_1$
,
![]() $\mathcal {L}_2$
be finite languages. The
$\mathcal {L}_2$
be finite languages. The
![]() $\mathcal {L}_2$
-theory
$\mathcal {L}_2$
-theory
![]() $T_2$
is hereditarily undecidable if there exist a finitely axiomatised essentially undecidable
$T_2$
is hereditarily undecidable if there exist a finitely axiomatised essentially undecidable
![]() $\mathcal {L}_1$
-theory
$\mathcal {L}_1$
-theory
![]() $T_1$
and models
$T_1$
and models
![]() $M_1 \models T_1$
,
$M_1 \models T_1$
,
![]() $M_2 \models T_2$
such that
$M_2 \models T_2$
such that
![]() $M_1$
is interpretable in
$M_1$
is interpretable in
![]() $M_2$
.
$M_2$
.
Proof This is [Reference Ershov, Lavrov, Taimanov and Taitslin15, pp. 87–89], using different (but equivalent) terminology. Results such as this originate in [Reference Tarski, Mostowski and Robinson46, Sections I.3 and I.4]; cf.Theorems 6–8 ibid.
We will use this as follows:
Lemma 1.7 [Reference Shoenfield44, Proposition 11.2]
Let
![]() $\mathcal {L}$
be a finite language and
$\mathcal {L}$
be a finite language and
![]() $a_1, \dots , a_n$
constant symbols not in
$a_1, \dots , a_n$
constant symbols not in
![]() $\mathcal {L}$
. Let M be an
$\mathcal {L}$
. Let M be an
![]() $\mathcal {L}(a_1, \dots , a_n)$
-structure and
$\mathcal {L}(a_1, \dots , a_n)$
-structure and
![]() $M|_{\mathcal {L}}$
the reduct of M to
$M|_{\mathcal {L}}$
the reduct of M to
![]() $\mathcal {L}$
. If
$\mathcal {L}$
. If
![]() ${\mathtt{Th}}(M; \mathcal {L}(a_1, \dots , a_n))$
is hereditarily undecidable, so too is
${\mathtt{Th}}(M; \mathcal {L}(a_1, \dots , a_n))$
is hereditarily undecidable, so too is
![]() ${\mathtt{Th}}(M|_{\mathcal {L}}; \mathcal {L})$
.
${\mathtt{Th}}(M|_{\mathcal {L}}; \mathcal {L})$
.
Corollary 1.8. Let K be a field of characteristic
![]() $0$
, and L a field of characteristic
$0$
, and L a field of characteristic
![]() $p> 0$
such that there exists
$p> 0$
such that there exists
![]() $t \in L$
transcendental over
$t \in L$
transcendental over
![]() $\mathbb {F}_p$
. Let
$\mathbb {F}_p$
. Let
![]() $\mathcal {L}$
be a finite expansion of the language of rings. Suppose
$\mathcal {L}$
be a finite expansion of the language of rings. Suppose
![]() $\operatorname {\mathbb {Z}}$
is
$\operatorname {\mathbb {Z}}$
is
![]() $\mathcal {L}$
-definable with parameters in K and
$\mathcal {L}$
-definable with parameters in K and
![]() $\mathbb {F}_p[t]$
is
$\mathbb {F}_p[t]$
is
![]() $\mathcal {L}$
-definable with parameters in L. Then
$\mathcal {L}$
-definable with parameters in L. Then
![]() $ {{\mathtt{Th}}}(K;\mathcal {L})$
and
$ {{\mathtt{Th}}}(K;\mathcal {L})$
and
![]() ${\mathtt{Th}}(L; \mathcal {L})$
are hereditarily undecidable.
${\mathtt{Th}}(L; \mathcal {L})$
are hereditarily undecidable.
Proof This is an application of Theorem 1.6
with
![]() $\mathcal {L}_2$
an expansion of
$\mathcal {L}_2$
an expansion of
![]() $\mathcal {L}$
by constant symbols,
$\mathcal {L}$
by constant symbols,
![]() $\mathcal {L}_1 = \mathcal {L}_r$
,
$\mathcal {L}_1 = \mathcal {L}_r$
,
![]() $T_1 = Q$
(Robinson arithmetic), and
$T_1 = Q$
(Robinson arithmetic), and
![]() $M_1 = \operatorname {\mathbb {N}}$
. Notice
$M_1 = \operatorname {\mathbb {N}}$
. Notice
![]() $\operatorname {\mathbb {N}}$
is
$\operatorname {\mathbb {N}}$
is
![]() $\emptyset $
-
$\emptyset $
-
![]() $\mathcal {L}_r$
-definable in
$\mathcal {L}_r$
-definable in
![]() $\operatorname {\mathbb {Z}}$
(e.g., by Lagrange’s Four Square Theorem) hence interpretable in
$\operatorname {\mathbb {Z}}$
(e.g., by Lagrange’s Four Square Theorem) hence interpretable in
![]() $\operatorname {\mathbb {Z}}$
. By [Reference Robinson41, Sections 4a and 4b],
$\operatorname {\mathbb {Z}}$
. By [Reference Robinson41, Sections 4a and 4b],
![]() $\operatorname {\mathbb {N}}$
is interpretable in the
$\operatorname {\mathbb {N}}$
is interpretable in the
![]() $\mathcal {L}_r(t)$
-structure
$\mathcal {L}_r(t)$
-structure
![]() $\mathbb {F}_p[t]$
. Thus, by assumption
$\mathbb {F}_p[t]$
. Thus, by assumption
![]() $\operatorname {\mathbb {N}}$
is interpretable in K (with, say, parameters
$\operatorname {\mathbb {N}}$
is interpretable in K (with, say, parameters
![]() $\overline {c} = \{c_1, \dots , c_k\}$
) and
$\overline {c} = \{c_1, \dots , c_k\}$
) and
![]() $\operatorname {\mathbb {N}}$
is interpretable in L (with, say, parameters
$\operatorname {\mathbb {N}}$
is interpretable in L (with, say, parameters
![]() $\overline {d} = \{d_1, \dots , d_l\}$
). By Theorem 1.6
,
$\overline {d} = \{d_1, \dots , d_l\}$
). By Theorem 1.6
,
![]() ${\mathtt{Th}}(K; \mathcal {L}(\overline {c}))$
and
${\mathtt{Th}}(K; \mathcal {L}(\overline {c}))$
and
![]() ${\mathtt{Th}}(L; \mathcal {L}(\overline {d}))$
are hereditarily undecidable. The hereditary undecidability of
${\mathtt{Th}}(L; \mathcal {L}(\overline {d}))$
are hereditarily undecidable. The hereditary undecidability of
![]() ${\mathtt{Th}}(K; \mathcal {L})$
and
${\mathtt{Th}}(K; \mathcal {L})$
and
![]() ${\mathtt{Th}}(L; \mathcal {L})$
follows from Lemma 1.7
exactly.
${\mathtt{Th}}(L; \mathcal {L})$
follows from Lemma 1.7
exactly.
Remark 1.9. Notational remark. By “
![]() $K \equiv _{\mathcal {L}} L$
” we denote that two
$K \equiv _{\mathcal {L}} L$
” we denote that two
![]() $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
![]() $K, L$
are elementarily equivalent. If “
$K, L$
are elementarily equivalent. If “
![]() $K \equiv L$
” is written, the language is implicitly
$K \equiv L$
” is written, the language is implicitly
![]() $\mathcal {L}_r$
. In the case of valued fields, we will frequently write “
$\mathcal {L}_r$
. In the case of valued fields, we will frequently write “
![]() $(K, v) \equiv (L, w)$
” to denote an
$(K, v) \equiv (L, w)$
” to denote an
![]() $\mathcal {L}_{val}$
-elementary equivalence, where
$\mathcal {L}_{val}$
-elementary equivalence, where
![]() $v, w$
are valuations on their respective fields.
$v, w$
are valuations on their respective fields.
2. First exploration by Ziegler
Ziegler’s main result of [Reference Ziegler49] is the construction of a field
![]() $K_q$
satisfying the following theorem:
$K_q$
satisfying the following theorem:
Theorem 2.1. Let L be the field
![]() $\operatorname {\mathbb {C}}$
,
$\operatorname {\mathbb {C}}$
,
![]() $\widetilde {\mathbb {F}_p(t)}$
,
$\widetilde {\mathbb {F}_p(t)}$
,
![]() $\operatorname {\mathbb {R}}$
, or
$\operatorname {\mathbb {R}}$
, or
![]() $\operatorname {\mathbb {Q}}_p$
, and
$\operatorname {\mathbb {Q}}_p$
, and
![]() $q \neq p$
prime. There exists a field
$q \neq p$
prime. There exists a field
![]() $K_q \subseteq L$
such that:
$K_q \subseteq L$
such that:
-
(1)
 $\operatorname {\mathbb {Z}}$
or
$\operatorname {\mathbb {Z}}$
or
 $\mathbb {F}_p[t]$
is definable (with parameters) in
$\mathbb {F}_p[t]$
is definable (with parameters) in
 $K_q$
.
$K_q$
. -
(2) If the intermediate field
 $K_q \subseteq H \subseteq L$
is finite over
$K_q \subseteq H \subseteq L$
is finite over
 $K_q$
, either
$K_q$
, either
 $[H : K_q] = 1$
or
$[H : K_q] = 1$
or
 $q | [H : K_q]$
.
$q | [H : K_q]$
.
Proof This is [Reference Ziegler49, Theorem, p. 270] with a specified A. Cf. Theorems 3.3 and 4.4, and Section 5, of [Reference Shlapentokh and Videla43] (this paper, by Shlapentokh and Videla, generalises Ziegler’s construction).
Corollary 2.2 (Ziegler)
Let p be prime. ACF
![]() ${}_0$
, ACF
${}_0$
, ACF
![]() ${}_p$
, RCF, and p
CF are finitely undecidable.
${}_p$
, RCF, and p
CF are finitely undecidable.
Proof [Reference Ziegler49, Corollary, p. 270]. Let T be a finite subtheory of L, which is one of the fields
![]() $\operatorname {\mathbb {C}}$
,
$\operatorname {\mathbb {C}}$
,
![]() $\widetilde {\mathbb {F}_p(t)}$
,
$\widetilde {\mathbb {F}_p(t)}$
,
![]() $\operatorname {\mathbb {R}}$
,
$\operatorname {\mathbb {R}}$
,
![]() $\operatorname {\mathbb {Q}}_p$
. Let P be the set of primes distinct to p. For each
$\operatorname {\mathbb {Q}}_p$
. Let P be the set of primes distinct to p. For each
![]() $q \in P$
, use Theorem 2.1
to obtain a field
$q \in P$
, use Theorem 2.1
to obtain a field
![]() $K_q$
satisfying (1) and (2). Let
$K_q$
satisfying (1) and (2). Let
![]() $\mathcal {U}$
be a nonprincipal ultrafilter on P, and let
$\mathcal {U}$
be a nonprincipal ultrafilter on P, and let
![]() $\mathbb {K}$
be the ultraproduct
$\mathbb {K}$
be the ultraproduct
![]() $\prod _{q \in P} K_q / \mathcal {U}$
.
$\prod _{q \in P} K_q / \mathcal {U}$
.
We claim that
![]() $\mathbb {K}$
is relatively algebraically closed in
$\mathbb {K}$
is relatively algebraically closed in
![]() $L^{\mathcal {U}}$
. Indeed, suppose
$L^{\mathcal {U}}$
. Indeed, suppose
![]() $f = (f_q) \in \mathbb {K}[X]$
has a root
$f = (f_q) \in \mathbb {K}[X]$
has a root
![]() $\alpha = (\alpha _q) \in L^{\mathcal {U}}$
. In which case,
$\alpha = (\alpha _q) \in L^{\mathcal {U}}$
. In which case,
![]() $\{q\mbox { : } f_q(\alpha _q) = 0\} \in \mathcal {U}$
, hence
$\{q\mbox { : } f_q(\alpha _q) = 0\} \in \mathcal {U}$
, hence
![]() $\{q\mbox { : } [K_q(\alpha _q) : K_q] \leq \deg (f)\} \in \mathcal {U}$
. Consequently, as
$\{q\mbox { : } [K_q(\alpha _q) : K_q] \leq \deg (f)\} \in \mathcal {U}$
. Consequently, as
![]() $q | [H : K_q]$
for all proper finite extensions
$q | [H : K_q]$
for all proper finite extensions
![]() $K_q \subset H \subseteq L$
,
$K_q \subset H \subseteq L$
,
![]() $\{q\mbox { : } [K_q(\alpha _q) : K_q] =1 \} \in \mathcal {U}$
. Hence
$\{q\mbox { : } [K_q(\alpha _q) : K_q] =1 \} \in \mathcal {U}$
. Hence
![]() $\alpha \in \mathbb {K}$
as desired.
$\alpha \in \mathbb {K}$
as desired.
By the model theory of algebraically/real closed/p-adically closed fields,Footnote
2
we deduce
![]() $\mathbb {K} \equiv L^{\mathcal {U}}$
(
$\mathbb {K} \equiv L^{\mathcal {U}}$
(
![]() $\equiv L$
by Łoś’ Theorem; specifically [Reference Chang and Keisler6, Theorem 4.1.9]). Therefore
$\equiv L$
by Łoś’ Theorem; specifically [Reference Chang and Keisler6, Theorem 4.1.9]). Therefore
![]() $\mathbb {K} \models T$
. As T is finitely axiomatised, by Łoś’ Theorem there must exist some
$\mathbb {K} \models T$
. As T is finitely axiomatised, by Łoś’ Theorem there must exist some
![]() $q \in P$
such that
$q \in P$
such that
![]() $K_q \models T$
. Thus by Theorem 2.1 and Corollary 1.8
,
$K_q \models T$
. Thus by Theorem 2.1 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_q; \mathcal {L}_r)$
is hereditarily undecidable, making T undecidable as required.
${\mathtt{Th}}(K_q; \mathcal {L}_r)$
is hereditarily undecidable, making T undecidable as required.
One can see the key step in this corollary was using the following property inherent to the considered fields L:
In Section 3 we will outline Ziegler’s construction of the field
![]() $K_q$
, with a minor discrepancy for L a separably closed field. In Section 4 we outline Ziegler’s construction in the case
$K_q$
, with a minor discrepancy for L a separably closed field. In Section 4 we outline Ziegler’s construction in the case
![]() $L=\operatorname {\mathbb {Q}}_p$
but again with minor changes, so his method works for a general class of henselian valued fields. Later in the paper we will discuss extending this construction to more difficult cases that avoid property
$L=\operatorname {\mathbb {Q}}_p$
but again with minor changes, so his method works for a general class of henselian valued fields. Later in the paper we will discuss extending this construction to more difficult cases that avoid property
![]() $(\flat )$
.
$(\flat )$
.
3. Separably closed fields
To save referring the reader to another text, we will outline Ziegler’s construction in this subsection. To make this a more interesting exercise we shall prove the theory of any separably closed field is finitely undecidable, not considered by Ziegler in [Reference Ziegler49].
Let SCF denote the theory of separably closed fields, SCF
![]() ${}_{p}$
the theory of separably closed fields of characteristic p, and SCF
${}_{p}$
the theory of separably closed fields of characteristic p, and SCF
![]() ${}_{p, e}$
the theory of separably closed fields of characteristic p and degree of imperfection e. We shall assume for this section the reader is familiar with [Reference Delon and Bouscaren11]. As SCF
${}_{p, e}$
the theory of separably closed fields of characteristic p and degree of imperfection e. We shall assume for this section the reader is familiar with [Reference Delon and Bouscaren11]. As SCF
![]() ${}_{0}\ =$
ACF
${}_{0}\ =$
ACF
![]() ${}_0$
and SCF
${}_0$
and SCF
![]() ${}_{p, 0}\ =$
ACF
${}_{p, 0}\ =$
ACF
![]() ${}_p$
, we will not consider the cases
${}_p$
, we will not consider the cases
![]() $p = 0$
or
$p = 0$
or
![]() $p> 0$
&
$p> 0$
&
![]() $e = 0$
(the case
$e = 0$
(the case
![]() $e = \infty $
will be considered separately in Corollary 3.8
).
$e = \infty $
will be considered separately in Corollary 3.8
).
Let
![]() $q \neq p$
be a prime number,
$q \neq p$
be a prime number,
![]() $L = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)\right )^s$
where
$L = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)\right )^s$
where
![]() $\{u_1, \dots , u_e\}$
are transcendental and algebraically independent over
$\{u_1, \dots , u_e\}$
are transcendental and algebraically independent over
![]() $\widetilde {\mathbb {F}_p(t)}$
(and “
$\widetilde {\mathbb {F}_p(t)}$
(and “
![]() $\,F^s\,$
‘’ denotes the separable closure of a field F). Note
$\,F^s\,$
‘’ denotes the separable closure of a field F). Note
![]() $L \models {\mathtt{SCF}}_{p,e}$
, as
$L \models {\mathtt{SCF}}_{p,e}$
, as
![]() $\widetilde {\mathbb {F}_p(t)}$
is perfect. First we have:
$\widetilde {\mathbb {F}_p(t)}$
is perfect. First we have:
Proposition 3.1. For each prime
![]() $q \neq p$
, there exists a field
$q \neq p$
, there exists a field
![]() $K_q \subseteq L$
such that:
$K_q \subseteq L$
such that:
-
(1)
 $\mathbb {F}_p[t]$
is definable (with parameters) in
$\mathbb {F}_p[t]$
is definable (with parameters) in
 $K_q$
.
$K_q$
. -
(2) If the intermediate field
 $K_q \subseteq H \subseteq L$
is finite and separable over
$K_q \subseteq H \subseteq L$
is finite and separable over
 $K_q$
, then
$K_q$
, then
 $[H : K_q] = 1$
or is divisible by q.
$[H : K_q] = 1$
or is divisible by q.
To prove this, we require a construction. Let
![]() $F = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_{e-1})\right )^s \subseteq L$
; we construct a field
$F = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_{e-1})\right )^s \subseteq L$
; we construct a field
![]() $K_q \subseteq L$
such that
$K_q \subseteq L$
such that
 $$ \begin{align*} F &= \{ a \in K_q \mbox{ : }\forall b \in K_q^* \mbox{ } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q] \rightarrow b \in (K_q)^q)\},\\ \mathbb{F}_p[t] &= \{r \in F \mbox{ : } \forall r_1 \neq r_2 \in F \mbox{ s.t. } r_1 + r_2 = r\mbox{, } u_e^q - r_1 \mbox{ or } u_e^q - r_2 \in (K_q)^q\}. \end{align*} $$
$$ \begin{align*} F &= \{ a \in K_q \mbox{ : }\forall b \in K_q^* \mbox{ } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q] \rightarrow b \in (K_q)^q)\},\\ \mathbb{F}_p[t] &= \{r \in F \mbox{ : } \forall r_1 \neq r_2 \in F \mbox{ s.t. } r_1 + r_2 = r\mbox{, } u_e^q - r_1 \mbox{ or } u_e^q - r_2 \in (K_q)^q\}. \end{align*} $$
This will suffice to prove Proposition 3.1(1). We will take
![]() $K_q$
to be the union of a sequence
$K_q$
to be the union of a sequence
within L of finite separable extensions
![]() $E_i/F(u_e)$
. Obtaining Proposition 3.1(2) while ensuring F and
$E_i/F(u_e)$
. Obtaining Proposition 3.1(2) while ensuring F and
![]() $\mathbb {F}_p[t]$
are definable in this way requires us to keep a tight rein on the q-th roots in
$\mathbb {F}_p[t]$
are definable in this way requires us to keep a tight rein on the q-th roots in
![]() $K_q$
. To that end, we will also carefully construct a sequence:
$K_q$
. To that end, we will also carefully construct a sequence:
of finite subsets
![]() $S_i \subseteq E_i$
, ultimately desiring
$S_i \subseteq E_i$
, ultimately desiring
![]() $K_q\setminus (K_q)^q = \bigcup _i S_i$
. To ensure we do not introduce an incompatibility between
$K_q\setminus (K_q)^q = \bigcup _i S_i$
. To ensure we do not introduce an incompatibility between
![]() $K_q \setminus (K_q)^q$
and F or
$K_q \setminus (K_q)^q$
and F or
![]() $\mathbb {F}_p[t]$
, we will ask the following rule [Reference Ziegler49, p. 273] to be obeyed at each point of the sequence
$\mathbb {F}_p[t]$
, we will ask the following rule [Reference Ziegler49, p. 273] to be obeyed at each point of the sequence
![]() $(E_i, S_i)$
:
$(E_i, S_i)$
:
 $$ \begin{align} & \mbox{There is a family of valuations}\ \{v_s\}_{s \in S_i}\ \mbox{on}\ E_i\ \mbox{such that}\ v_s(F) = 0\ \mbox{and} \nonumber\\ & q \nmid v_s(s)\ \mbox{for}\ s \in S_i.\ \mbox{In addition, for all}\ r_1 \neq r_2 \in F\ \mbox{with}\ r_1 + r_2 \in \mathbb{F}_p[t], \hspace{7mm} \\ &\mbox{either}\ \forall s\ \in S_i,\ q | v_s(u_e^q - r_1),\ \text{or}\ \forall s \in S_i,\ q | v_s(u_e^q - r_2). \nonumber \end{align} $$
$$ \begin{align} & \mbox{There is a family of valuations}\ \{v_s\}_{s \in S_i}\ \mbox{on}\ E_i\ \mbox{such that}\ v_s(F) = 0\ \mbox{and} \nonumber\\ & q \nmid v_s(s)\ \mbox{for}\ s \in S_i.\ \mbox{In addition, for all}\ r_1 \neq r_2 \in F\ \mbox{with}\ r_1 + r_2 \in \mathbb{F}_p[t], \hspace{7mm} \\ &\mbox{either}\ \forall s\ \in S_i,\ q | v_s(u_e^q - r_1),\ \text{or}\ \forall s \in S_i,\ q | v_s(u_e^q - r_2). \nonumber \end{align} $$
We will reference the following two standard lemmas, taken directly from [Reference Ziegler49, Section 3]:
Lemma 3.2 [Reference Ziegler49, Lemma 1]
Let
![]() $(H_1, v_1)$
be a discretely valued field,
$(H_1, v_1)$
be a discretely valued field,
![]() $H_2/H_1$
a finite extension, and q a prime such that
$H_2/H_1$
a finite extension, and q a prime such that
![]() $q \nmid [H_2 : H_1]$
. Then there is an extension of
$q \nmid [H_2 : H_1]$
. Then there is an extension of
![]() $v_1$
to
$v_1$
to
![]() $H_2$
, which we denote
$H_2$
, which we denote
![]() $v_2$
, such that
$v_2$
, such that
![]() $q \nmid (v_2 H_2 : v_1 H_1)$
.
$q \nmid (v_2 H_2 : v_1 H_1)$
.
Lemma 3.3 [Reference Ziegler49, Lemma 2]
Let
![]() $(H, v)$
be a valued field and q a prime distinct to
$(H, v)$
be a valued field and q a prime distinct to
![]() $\operatorname {\mathrm {char}}(Hv)$
. For
$\operatorname {\mathrm {char}}(Hv)$
. For
![]() $a \in H \setminus (H)^q$
with
$a \in H \setminus (H)^q$
with
![]() $q | v(a)$
, there is an extension of valued fields
$q | v(a)$
, there is an extension of valued fields
![]() $(H(\sqrt [q]{a}), w)/(H, v)$
such that
$(H(\sqrt [q]{a}), w)/(H, v)$
such that
![]() $wH(\sqrt [q]{a}) = vH$
.
$wH(\sqrt [q]{a}) = vH$
.
We will also require the following fact:
Definition 3.4. Valuations
![]() $v_1, v_2$
on a field K are dependent if
$v_1, v_2$
on a field K are dependent if
![]() $\mathcal {O}_{v_1} \mathcal {O}_{v_2} \subsetneq K$
.
$\mathcal {O}_{v_1} \mathcal {O}_{v_2} \subsetneq K$
.
Lemma 3.5. If
![]() $v_1, v_2$
are dependent discrete valuations on a field K, then
$v_1, v_2$
are dependent discrete valuations on a field K, then
![]() $v_1 = v_2$
(by which we mean
$v_1 = v_2$
(by which we mean
![]() $\mathcal {O}_{v_1} = \mathcal {O}_{v_2})$
.
$\mathcal {O}_{v_1} = \mathcal {O}_{v_2})$
.
Proof The valuation ring of a discrete valuation is maximal [Reference Engler and Prestel13, Corollary 2.3.2], hence
![]() $\mathcal {O}_{v_1} = \mathcal {O}_{v_1}\mathcal {O}_{v_2} = \mathcal {O}_{v_2}$
as desired.
$\mathcal {O}_{v_1} = \mathcal {O}_{v_1}\mathcal {O}_{v_2} = \mathcal {O}_{v_2}$
as desired.
The construction begins with an enumeration
![]() $a_0, a_1, a_2, \dots $
of the elements of L separably algebraic over
$a_0, a_1, a_2, \dots $
of the elements of L separably algebraic over
![]() $F(u_e)$
, each repeated countably infinitely many times. Suppose
$F(u_e)$
, each repeated countably infinitely many times. Suppose
![]() $(E_i, S_i)$
is already constructed—Ziegler considers now four cases, based on the equivalence class of i mod
$(E_i, S_i)$
is already constructed—Ziegler considers now four cases, based on the equivalence class of i mod
![]() $4$
. These correspond to guaranteeing Proposition 3.1(1) (Case 1), Proposition 3.1(2) (Case 2), the definition of F by ensuring there is a “reason” b is excluded from
$4$
. These correspond to guaranteeing Proposition 3.1(1) (Case 1), Proposition 3.1(2) (Case 2), the definition of F by ensuring there is a “reason” b is excluded from
![]() $(K_q)^q$
(Case 3 +
$(K_q)^q$
(Case 3 +
![]() $\clubsuit $
), and the definition of
$\clubsuit $
), and the definition of
![]() $\mathbb {F}_p[t]$
(Case 4 +
$\mathbb {F}_p[t]$
(Case 4 +
![]() $\clubsuit $
); again, by ensuring there is a “reason”
$\clubsuit $
); again, by ensuring there is a “reason”
![]() $a_n$
is excluded.
$a_n$
is excluded.
Construction. (cf. [Reference Ziegler49, Section 3])
Case 1:
![]() $i = 4n$
. If
$i = 4n$
. If
![]() $q | [E_i(a_n) : E_i]$
, then
$q | [E_i(a_n) : E_i]$
, then
![]() $(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise set
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise set
![]() $(E_{i+1}, S_{i+1})\ = (E_i(a_n), S_i)$
and using Lemma 3.2
extend each valuation
$(E_{i+1}, S_{i+1})\ = (E_i(a_n), S_i)$
and using Lemma 3.2
extend each valuation
![]() $v_s$
,
$v_s$
,
![]() $s \in S_i$
, from
$s \in S_i$
, from
![]() $E_i$
to
$E_i$
to
![]() $E_{i+1}$
in a way preserving
$E_{i+1}$
in a way preserving
![]() $(\clubsuit )$
.
$(\clubsuit )$
.
Case 2:
![]() $i = 4n + 1$
. Unless
$i = 4n + 1$
. Unless
![]() $a_n \in E_i \setminus S_i$
, set
$a_n \in E_i \setminus S_i$
, set
![]() $(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise, if for some
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise, if for some
![]() $v_s$
,
$v_s$
,
![]() $s \in S_i$
, we have
$s \in S_i$
, we have
![]() $q \nmid v_s(a_n)$
then define
$q \nmid v_s(a_n)$
then define
![]() $(E_{i+1}, S_{i+1})= (E_i, S_i \cup \{a_n\})$
and set
$(E_{i+1}, S_{i+1})= (E_i, S_i \cup \{a_n\})$
and set
![]() $v_{a_n} \mathrel {\mathop :}= v_s$
. This ensures
$v_{a_n} \mathrel {\mathop :}= v_s$
. This ensures
![]() $(\clubsuit )$
holds for
$(\clubsuit )$
holds for
![]() $i+1$
. If
$i+1$
. If
![]() $q| v_s(a_n)$
for all
$q| v_s(a_n)$
for all
![]() $s \in S_i$
, then we take
$s \in S_i$
, then we take
![]() $(E_{i+1}, S_{i+1}) = (E_i(\sqrt [q]{a_n}), S_i)$
Footnote
3
and extend every valuation according to Lemma 3.3
.
$(E_{i+1}, S_{i+1}) = (E_i(\sqrt [q]{a_n}), S_i)$
Footnote
3
and extend every valuation according to Lemma 3.3
.
Case 3:
![]() $i = 4n +2$
. Unless
$i = 4n +2$
. Unless
![]() $a_n \in E_i \setminus F$
, let
$a_n \in E_i \setminus F$
, let
![]() $(E_{i+1}, S_{i+1})= (E_i, S_i)$
. If
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. If
![]() $a_n \in E_i \setminus F$
let v be a discrete valuation on
$a_n \in E_i \setminus F$
let v be a discrete valuation on
![]() $E_i$
, trivial on F, which is negative on
$E_i$
, trivial on F, which is negative on
![]() $a_n$
. If the second condition in
$a_n$
. If the second condition in
![]() $(\clubsuit )$
does not already hold for
$(\clubsuit )$
does not already hold for
![]() $\{v, \{v_s\}_{s \in S_i}\}$
in
$\{v, \{v_s\}_{s \in S_i}\}$
in
![]() $E_i$
, then there exists
$E_i$
, then there exists
![]() $r \in F$
such that
$r \in F$
such that
![]() $q \nmid v(u_e^q - r)$
and
$q \nmid v(u_e^q - r)$
and
![]() $q | v_s(u_e^q - r)$
for all
$q | v_s(u_e^q - r)$
for all
![]() $s \in S_i$
. By the strong triangle inequality, there is at most one such r: indeed, for
$s \in S_i$
. By the strong triangle inequality, there is at most one such r: indeed, for
![]() $r \neq r' \in F$
,
$r \neq r' \in F$
,
![]() $v(u_e^q - r') = v(u_e^q - r + r - r') = 0$
, as
$v(u_e^q - r') = v(u_e^q - r + r - r') = 0$
, as
![]() $v(r - r') = 0$
and
$v(r - r') = 0$
and
![]() $q \nmid v(u_e^q - r)$
. As
$q \nmid v(u_e^q - r)$
. As
![]() $L = (L)^q$
, we may set
$L = (L)^q$
, we may set
![]() $E = E_i(\sqrt [q]{u_e^q - r})$
and extend the valuations
$E = E_i(\sqrt [q]{u_e^q - r})$
and extend the valuations
![]() $\{v, \{v_s\}_{s \in S_i}\}$
sensibly as above. We conclude the second condition of
$\{v, \{v_s\}_{s \in S_i}\}$
sensibly as above. We conclude the second condition of
![]() $(\clubsuit )$
holds for
$(\clubsuit )$
holds for
![]() $(E, \{v, \{v_s\}_{s \in S_i}\})$
.
$(E, \{v, \{v_s\}_{s \in S_i}\})$
.
If v is independent to
![]() $v_s$
for every
$v_s$
for every
![]() $s \in S_i$
: let
$s \in S_i$
: let
![]() $\{v, v_{s_1}, \dots , v_{s_k}\}$
be the distinct valuations of
$\{v, v_{s_1}, \dots , v_{s_k}\}$
be the distinct valuations of
![]() $\{v, \{v_s\}_{s \in S_i}\}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
$\{v, \{v_s\}_{s \in S_i}\}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
![]() $b \in E$
such that
$b \in E$
such that
![]() $v(b)$
is the smallest positive element in the value group of v (hence
$v(b)$
is the smallest positive element in the value group of v (hence
![]() $q | v(1+b)$
,
$q | v(1+b)$
,
![]() $q|v(a_n^q + b^{-1})$
) and
$q|v(a_n^q + b^{-1})$
) and
![]() $q|v_{s_j}(b)$
,
$q|v_{s_j}(b)$
,
![]() $q|v_{s_j}(1+b)$
,
$q|v_{s_j}(1+b)$
,
![]() $q|v_{s_j}(a_n^q + b^{-1})$
for
$q|v_{s_j}(a_n^q + b^{-1})$
for
![]() $1 \leq j \leq k$
. As
$1 \leq j \leq k$
. As
![]() $b, 1+b, a_n^q + b^{-1} \in (L)^q = L$
, we may define
$b, 1+b, a_n^q + b^{-1} \in (L)^q = L$
, we may define
Extending
![]() $\{v_b = v, \{v_s\}_{s \in S_i}\}$
as above, we know
$\{v_b = v, \{v_s\}_{s \in S_i}\}$
as above, we know
![]() $(\clubsuit )$
holds as it did on E.
$(\clubsuit )$
holds as it did on E.
If v is dependent with
![]() $v_{\widehat {s}}$
for some
$v_{\widehat {s}}$
for some
![]() $\widehat {s} \in S_i$
: by Lemma 3.5
$\widehat {s} \in S_i$
: by Lemma 3.5
![]() $v = v_{\widehat {s}}$
. Let
$v = v_{\widehat {s}}$
. Let
![]() $\{v_{s_1}, \dots , v_{s_l}\}$
be the distinct valuations of
$\{v_{s_1}, \dots , v_{s_l}\}$
be the distinct valuations of
![]() $\{v, \{v_s\}_{s \in S_i}\}$
, assuming WLOG
$\{v, \{v_s\}_{s \in S_i}\}$
, assuming WLOG
![]() $v = v_{s_1}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
$v = v_{s_1}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
![]() $b \in E$
such that
$b \in E$
such that
![]() $v_{s_1}(b)$
is the smallest positive element in the value group of
$v_{s_1}(b)$
is the smallest positive element in the value group of
![]() $v_{s_1}$
, and
$v_{s_1}$
, and
![]() $q|v_{s_j}(b)$
,
$q|v_{s_j}(b)$
,
![]() $q|v_{s_j}(1+b)$
,
$q|v_{s_j}(1+b)$
,
![]() $q|v_{s_j}(a_n^q + b^{-1})$
for
$q|v_{s_j}(a_n^q + b^{-1})$
for
![]() $2 \leq j \leq l$
. As
$2 \leq j \leq l$
. As
![]() $b, 1+b, a_n^q + b^{-1} \in (L)^q = L$
, we may define
$b, 1+b, a_n^q + b^{-1} \in (L)^q = L$
, we may define
Extending
![]() $\{v_b = v_{s_1}, \{v_s\}_{s \in S_i}\}$
as above, again
$\{v_b = v_{s_1}, \{v_s\}_{s \in S_i}\}$
as above, again
![]() $(\clubsuit )$
holds on
$(\clubsuit )$
holds on
![]() $(E_{i+1}, S_{i+1})$
. (This case allows
$(E_{i+1}, S_{i+1})$
. (This case allows
![]() $b \in S_i$
without issue, by Lemma 3.5
.)
$b \in S_i$
without issue, by Lemma 3.5
.)
Case 4:
![]() $i = 4n+3$
. Unless
$i = 4n+3$
. Unless
![]() $a_n \in F\setminus \mathbb {F}_p[t]$
we set
$a_n \in F\setminus \mathbb {F}_p[t]$
we set
![]() $(E_{i+1}, S_{i+1}) = (E_{i}, S_{i})$
. Otherwise, first observe
$(E_{i+1}, S_{i+1}) = (E_{i}, S_{i})$
. Otherwise, first observe
![]() $B = \{r \in F \mbox { : } \exists s \in S_i \mbox { s.t. } q \nmid v_s(u_e^q - r)\}$
is finite. Next, for
$B = \{r \in F \mbox { : } \exists s \in S_i \mbox { s.t. } q \nmid v_s(u_e^q - r)\}$
is finite. Next, for
![]() $r \in F^*$
there exists a discrete valuation
$r \in F^*$
there exists a discrete valuation
![]() $v_r$
on
$v_r$
on
![]() $F(u_e)$
, trivial on F, for which
$F(u_e)$
, trivial on F, for which
![]() $v_r(u_e^q - r)$
is the smallest positive element of its valuation group (this follows as
$v_r(u_e^q - r)$
is the smallest positive element of its valuation group (this follows as
![]() $X^q - r \in F[X]$
has no multiple factors). For each such r, we choose an extension
$X^q - r \in F[X]$
has no multiple factors). For each such r, we choose an extension
![]() $w_r$
of
$w_r$
of
![]() $v_r$
to
$v_r$
to
![]() $E_i$
, and by the construction of
$E_i$
, and by the construction of
![]() $E_i/F$
, the set
$E_i/F$
, the set
![]() $C =$
$C =$
![]() $\{r \in F^* \mbox { : } q|w_r(u_e^q - r)\}$
is finite. Choose
$\{r \in F^* \mbox { : } q|w_r(u_e^q - r)\}$
is finite. Choose
![]() $r_1 \in F^*$
such that
$r_1 \in F^*$
such that
![]() $r_1 \neq a_n$
,
$r_1 \neq a_n$
,
![]() $2 r_1 \neq a_n$
, and
$2 r_1 \neq a_n$
, and
![]() $r_1, a_n -r_1 \not \in C$
, and
$r_1, a_n -r_1 \not \in C$
, and
![]() $r_1, a_n - r_1 \not \in \mathbb {F}_p[t]$
. Let
$r_1, a_n - r_1 \not \in \mathbb {F}_p[t]$
. Let
![]() $r_2 = a_n - r_1$
and finally define
$r_2 = a_n - r_1$
and finally define
One can prove
![]() $\{w_{r_1}, w_{r_2}, \{v_s\}_{s \in S_i}\}$
satisfies
$\{w_{r_1}, w_{r_2}, \{v_s\}_{s \in S_i}\}$
satisfies
![]() $(\clubsuit )$
based on this construction.⊣
$(\clubsuit )$
based on this construction.⊣
Lemma 3.6. Set
![]() $K_q = \bigcup _i E_i$
. The above construction ensures we have the following features of
$K_q = \bigcup _i E_i$
. The above construction ensures we have the following features of
![]() $K_q$
, and the definitions of F and
$K_q$
, and the definitions of F and
![]() $\mathbb {F}_p[t]$
we intended:
$\mathbb {F}_p[t]$
we intended:
-
(1)
 $F \subseteq (K_q)^q$
.
$F \subseteq (K_q)^q$
. -
(2)
 $K_q \setminus (K_q)^q = \bigcup _i S_i$
.
$K_q \setminus (K_q)^q = \bigcup _i S_i$
. -
(3)
 $F = \{a \in K_q : \forall b \in K_q^* \mbox { } [( 1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q) \rightarrow b \in (K_q)^q]\}$
.
$F = \{a \in K_q : \forall b \in K_q^* \mbox { } [( 1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q) \rightarrow b \in (K_q)^q]\}$
. -
(4)
 $\mathbb {F}_p[t]\! =\! \{r \in F\! :\! \forall r_1 \neq r_2 \in F\! \mbox { } (r_1 + r_2 = r)\! \rightarrow \! (u_e^q - r_1\! \in \! (K_q)^q \lor u_e^q - r_2\! \in \! (K_q)^q)\}$
.
$\mathbb {F}_p[t]\! =\! \{r \in F\! :\! \forall r_1 \neq r_2 \in F\! \mbox { } (r_1 + r_2 = r)\! \rightarrow \! (u_e^q - r_1\! \in \! (K_q)^q \lor u_e^q - r_2\! \in \! (K_q)^q)\}$
.
Proof We follow [Reference Ziegler49, Section 4] as much as possible.
-
(1) As F is separably closed, and
 $q \neq p$
,
$q \neq p$
,
 $F = (F)^q$
.
$F = (F)^q$
. -
(2) Let
 $a \in (K_q)^q$
. For all sufficiently large i,
$a \in (K_q)^q$
. For all sufficiently large i,
 $a \in (E_i)^q$
; hence
$a \in (E_i)^q$
; hence
 $q | v(a)$
for all v trivial on F. Therefore by
$q | v(a)$
for all v trivial on F. Therefore by
 $(\clubsuit )$
we have
$(\clubsuit )$
we have
 $a \not \in S_i$
; consequently
$a \not \in S_i$
; consequently
 $a \not \in \bigcup _i S_i$
. Conversely if
$a \not \in \bigcup _i S_i$
. Conversely if
 $a \in K_q\setminus (K_q)^q$
, then for some n sufficiently large we have
$a \in K_q\setminus (K_q)^q$
, then for some n sufficiently large we have
 $a = a_n$
and
$a = a_n$
and
 $a \in E_{4n+1}$
. By Case 2 of the construction,
$a \in E_{4n+1}$
. By Case 2 of the construction,
 $a \in S_{4n+2}$
. This proves
$a \in S_{4n+2}$
. This proves
 $K_q \setminus (K_q)^q = \bigcup _i S_i$
.
$K_q \setminus (K_q)^q = \bigcup _i S_i$
. -
(3) Fix
 $a \in F$
. Suppose for some nonzero
$a \in F$
. Suppose for some nonzero
 $b \in K_q$
that
$b \in K_q$
that
 $1 + b, a^q + b^{-1} \in (K_q)^q$
. Let i be so large that
$1 + b, a^q + b^{-1} \in (K_q)^q$
. Let i be so large that
 $1+b, a^q + b^{-1} \in (E_i)^q$
. Let v be any valuation on
$1+b, a^q + b^{-1} \in (E_i)^q$
. Let v be any valuation on
 $E_i$
that is trivial on F. If
$E_i$
that is trivial on F. If
 $v(b)> 0$
, then
$v(b)> 0$
, then
 $v(b) = -v(a^q + b^{-1})$
is divisible by q. If
$v(b) = -v(a^q + b^{-1})$
is divisible by q. If
 $v(b) < 0$
, then
$v(b) < 0$
, then
 $v(b) = v(1+b)$
is divisible by q. Hence
$v(b) = v(1+b)$
is divisible by q. Hence
 $q| v(b)$
always. By
$q| v(b)$
always. By
 $(\clubsuit )$
,
$(\clubsuit )$
,
 $b \not \in S_i$
; by (2) therefore
$b \not \in S_i$
; by (2) therefore
 $b \in (K_q)^q$
. Conversely, if
$b \in (K_q)^q$
. Conversely, if
 $a \in K_q \setminus F$
, we may choose n sufficiently large such that
$a \in K_q \setminus F$
, we may choose n sufficiently large such that
 $a = a_n \in E_{4n+2}$
. In Case 3 we make it such that in
$a = a_n \in E_{4n+2}$
. In Case 3 we make it such that in
 $S_{4n+3}$
there is a (nonzero) b with
$S_{4n+3}$
there is a (nonzero) b with
 $1 + b, a^q + b^{-1} \in (E_{4n+3})^q$
. This concludes the proof.
$1 + b, a^q + b^{-1} \in (E_{4n+3})^q$
. This concludes the proof. -
(4) Let
 $r_1 + r_2 \in \mathbb {F}_p[t]$
, with
$r_1 + r_2 \in \mathbb {F}_p[t]$
, with
 $r_1 \neq r_2 \in F$
. If it is the case that
$r_1 \neq r_2 \in F$
. If it is the case that
 $u_e^q - r_1, u_e^q - r_2 \not \in (K_q)^q$
, then for some sufficiently large i, they belong to
$u_e^q - r_1, u_e^q - r_2 \not \in (K_q)^q$
, then for some sufficiently large i, they belong to
 $S_i$
. However this contradicts
$S_i$
. However this contradicts
 $(\clubsuit )$
. If we suppose
$(\clubsuit )$
. If we suppose
 $r \in F \setminus \mathbb {F}_p[t]$
, for some sufficiently large n it is the case that
$r \in F \setminus \mathbb {F}_p[t]$
, for some sufficiently large n it is the case that
 $a_n = r$
. Then by Case 4 there exists
$a_n = r$
. Then by Case 4 there exists
 $r_1 \neq r_2 \in F$
,
$r_1 \neq r_2 \in F$
,
 $r_1 + r_2 = r$
, such that
$r_1 + r_2 = r$
, such that
 $u_e^q - r_1, u_e^q - r_2 \in S_{4n+4}$
. By (2) this ensures
$u_e^q - r_1, u_e^q - r_2 \in S_{4n+4}$
. By (2) this ensures
 $u_e^q - r_1, u_e^q - r_2 \not \in (K_q)^q$
; again a contradiction.
$u_e^q - r_1, u_e^q - r_2 \not \in (K_q)^q$
; again a contradiction.
Proof of Proposition 3.1
First, as F and
![]() $\mathbb {F}_p[t]$
are definable,
$\mathbb {F}_p[t]$
are definable,
![]() $\operatorname {\mathbb {N}}$
is interpretable (with parameters) as an
$\operatorname {\mathbb {N}}$
is interpretable (with parameters) as an
![]() $\mathcal {L}_r$
-structure in
$\mathcal {L}_r$
-structure in
![]() $K_q$
. Next, note that
$K_q$
. Next, note that
![]() $K_q/F(u_e)$
is a separable extension, as by construction it is a union of finite separable extensions, and
$K_q/F(u_e)$
is a separable extension, as by construction it is a union of finite separable extensions, and
![]() $K_q \subseteq F(u_e)^s$
. Let
$K_q \subseteq F(u_e)^s$
. Let
![]() $K_q \subset H \subseteq L$
be a finite separable extension. Then
$K_q \subset H \subseteq L$
be a finite separable extension. Then
![]() $H = K_q(a)$
for some
$H = K_q(a)$
for some
![]() $a \in L$
by the Primitive Element Theorem. As
$a \in L$
by the Primitive Element Theorem. As
![]() $K_q(a)/F(u_e)$
is separable, for some n sufficiently large we have
$K_q(a)/F(u_e)$
is separable, for some n sufficiently large we have
![]() $a = a_{n}$
and
$a = a_{n}$
and
as we assume
![]() $a \not \in K_q$
. By construction,
$a \not \in K_q$
. By construction,
![]() $q | [E_{4n}(a) : E_{4n}]$
.
$q | [E_{4n}(a) : E_{4n}]$
.
Combining these fields in a nonprincipal ultraproduct, as will be done in the next corollary, allows us to conclude the desired undecidability result.
Corollary 3.7. Let p be a prime and
![]() $e \in \operatorname {\mathbb {N}}_{>0}$
. Then
SCF
$e \in \operatorname {\mathbb {N}}_{>0}$
. Then
SCF
![]() ${}_{p, e}$
is finitely undecidable.
${}_{p, e}$
is finitely undecidable.
Proof Let
![]() $L = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)\right )^s$
as before Proposition 3.1
. Let P be the set of primes distinct to p. For each
$L = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)\right )^s$
as before Proposition 3.1
. Let P be the set of primes distinct to p. For each
![]() $q \in P$
, use Proposition 3.1
to obtain a field
$q \in P$
, use Proposition 3.1
to obtain a field
![]() $K_q$
satisfying (1) and (2) ibid. Let
$K_q$
satisfying (1) and (2) ibid. Let
![]() $\mathcal {U}$
be a nonprincipal ultrafilter on P and let
$\mathcal {U}$
be a nonprincipal ultrafilter on P and let
![]() $\mathbb {K}$
be the ultraproduct
$\mathbb {K}$
be the ultraproduct
![]() $\prod _{q \in P} K_q / \mathcal {U}$
. We claim that
$\prod _{q \in P} K_q / \mathcal {U}$
. We claim that
![]() $\mathbb {K}$
is relatively separably closed in
$\mathbb {K}$
is relatively separably closed in
![]() $L^{\mathcal {U}}$
: indeed, suppose
$L^{\mathcal {U}}$
: indeed, suppose
![]() $f = (f_q) \in \mathbb {K}[X]$
is separable and has a root
$f = (f_q) \in \mathbb {K}[X]$
is separable and has a root
![]() $\alpha = (\alpha _q) \in L^{\mathcal {U}}$
. In which case
$\alpha = (\alpha _q) \in L^{\mathcal {U}}$
. In which case
 $$ \begin{align*} &\{q \mbox{ : } f_q(x) \in K_q[X] \mbox{ separable, and } f_q(\alpha_q) = 0\} \in \mathcal{U},\\ \mbox{hence }&\{q \mbox{ : } K_q(\alpha_q)/K_q \mbox{ separable and } [K_q(\alpha_q) : K_q] \leq \deg(f)\} \in \mathcal{U}. \end{align*} $$
$$ \begin{align*} &\{q \mbox{ : } f_q(x) \in K_q[X] \mbox{ separable, and } f_q(\alpha_q) = 0\} \in \mathcal{U},\\ \mbox{hence }&\{q \mbox{ : } K_q(\alpha_q)/K_q \mbox{ separable and } [K_q(\alpha_q) : K_q] \leq \deg(f)\} \in \mathcal{U}. \end{align*} $$
By Proposition 3.1(2),
![]() $\{q \mbox { : } [K_q(\alpha _a) : K_q] = 1\} \in \mathcal {U}$
, and thus
$\{q \mbox { : } [K_q(\alpha _a) : K_q] = 1\} \in \mathcal {U}$
, and thus
![]() $\alpha \in \mathbb {K}$
as desired.
$\alpha \in \mathbb {K}$
as desired.
Therefore
![]() $\mathbb {K}$
is a separably closed field of characteristic p. Recall
$\mathbb {K}$
is a separably closed field of characteristic p. Recall
![]() $\{u_1, \dots , u_e\}$
is a p-basis for L. As they are p-independent in L, and by construction
$\{u_1, \dots , u_e\}$
is a p-basis for L. As they are p-independent in L, and by construction
![]() $u_1, \dots , u_{e} \in K_q$
, they remain p-independent in
$u_1, \dots , u_{e} \in K_q$
, they remain p-independent in
![]() $K_q$
. Hence the degree of imperfection of
$K_q$
. Hence the degree of imperfection of
![]() $K_q$
is at least e, for each q. Moreover, by construction
$K_q$
is at least e, for each q. Moreover, by construction
![]() $K_q /\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)$
is an algebraic (separable) extension. As algebraic extensions do not increase the degree of imperfection, the degree of imperfection of
$K_q /\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)$
is an algebraic (separable) extension. As algebraic extensions do not increase the degree of imperfection, the degree of imperfection of
![]() $K_q$
is at most e. Thus by Łoś’ Theorem, the degree of imperfection of
$K_q$
is at most e. Thus by Łoś’ Theorem, the degree of imperfection of
![]() $\mathbb {K}$
is exactly e. We conclude that
$\mathbb {K}$
is exactly e. We conclude that
![]() $\mathbb {K} \models {\mathtt {SCF}}_{p, e}$
, and hence
$\mathbb {K} \models {\mathtt {SCF}}_{p, e}$
, and hence
![]() $\mathbb {K} \models T$
for any finite subtheory
$\mathbb {K} \models T$
for any finite subtheory
![]() $T \subseteq {\mathtt {SCF}}_{p, e}$
.
$T \subseteq {\mathtt {SCF}}_{p, e}$
.
Since T is finitely axiomatised, there exists some prime q such that
![]() $K_q \models T$
. By Lemma 3.6 and Corollary 1.8
,
$K_q \models T$
. By Lemma 3.6 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_q; \mathcal {L}_r)$
is hereditarily undecidable, making T undecidable as required.
${\mathtt{Th}}(K_q; \mathcal {L}_r)$
is hereditarily undecidable, making T undecidable as required.
Corollary 3.8. Let p be prime. Then
SCF
![]() ${}_{p, \infty }$
is finitely undecidable.
${}_{p, \infty }$
is finitely undecidable.
Proof Let T be a finite subtheory of SCF
![]() ${}_{p, \infty }$
, which we assume is axiomatised by the axioms of a field of characteristic p, such that each separable polynomial over the field has a root in the field, and for each
${}_{p, \infty }$
, which we assume is axiomatised by the axioms of a field of characteristic p, such that each separable polynomial over the field has a root in the field, and for each
![]() $n \in \operatorname {\mathbb {N}}_{>0}$
the statement “the degree of imperfection is greater than n.” By the Compactness Theorem, there exists a finite subset
$n \in \operatorname {\mathbb {N}}_{>0}$
the statement “the degree of imperfection is greater than n.” By the Compactness Theorem, there exists a finite subset
![]() $\Delta $
of this axiomatisation such that
$\Delta $
of this axiomatisation such that
![]() $\Delta \models T$
. For some finite
$\Delta \models T$
. For some finite
![]() $\nu $
sufficiently large, SCF
$\nu $
sufficiently large, SCF
![]() ${}_{p, \nu } \models \Delta $
; hence T is a finite subtheory of SCF
${}_{p, \nu } \models \Delta $
; hence T is a finite subtheory of SCF
![]() ${}_{p, \nu }$
. The result follows from Corollary 3.7
.
${}_{p, \nu }$
. The result follows from Corollary 3.7
.
Example 3.9. For all primes
![]() $p> 0$
and
$p> 0$
and
![]() $e \in \operatorname {\mathbb {N}} \cup \,\{\infty \}$
, the theory
$e \in \operatorname {\mathbb {N}} \cup \,\{\infty \}$
, the theory
![]() ${\mathtt{SCF}}_{p,e}$
is known to be decidable (see [Reference Delon and Bouscaren11, pp. 146–153] for exposition). Therefore Corollaries 3.7 and 3.8
put a bound on further possible decidability results for these theories.
${\mathtt{SCF}}_{p,e}$
is known to be decidable (see [Reference Delon and Bouscaren11, pp. 146–153] for exposition). Therefore Corollaries 3.7 and 3.8
put a bound on further possible decidability results for these theories.
It is worth remarking that, modulo some conjectures, these results are in connection with aspects of classification theory. It is a theorem of Macintyre [Reference Macintyre35] that every infinite
![]() $\omega $
-stable field is a model of ACF
$\omega $
-stable field is a model of ACF
![]() ${}_p$
for
${}_p$
for
![]() $p = 0$
or prime. From the 1970s we have the following conjecture:
$p = 0$
or prime. From the 1970s we have the following conjecture:
Conjecture (Stable Fields)
Every infinite stable field is separably closed.
This is known in some cases, such as for the aforementioned
![]() $\omega $
-stable [Reference Macintyre35] or superstable infinite fields [Reference Cherlin and Shelah7], or for infinite stable fields of weight 1 [Reference Krupiński and Pillay34] or finite dp-rank [Reference Halevi and Palacín18], or most recently infinite large stable fields [Reference Johnson, Tran, Walsberg and Ye30].
$\omega $
-stable [Reference Macintyre35] or superstable infinite fields [Reference Cherlin and Shelah7], or for infinite stable fields of weight 1 [Reference Krupiński and Pillay34] or finite dp-rank [Reference Halevi and Palacín18], or most recently infinite large stable fields [Reference Johnson, Tran, Walsberg and Ye30].
Corollary 3.10. Assume the Stable Fields Conjecture. Then every infinite stable field is finitely undecidable.
Let us use this connection to classification theory to motivate which fields to consider next. Outside of stable theories, there are two orthogonal directions in which to travel: one direction attempts to extend the theories of forking, dividing and independence of types to more general contexts (e.g., [super]simple and [super]rosy), while the other direction aims to understand theories with a modest notion of order (e.g., o-minimal and NIP). The latter direction contains theories we are already familiar with: RCF in the language of ordered rings is o-minimal, and p CF in the language of valued fields is distal and dp-minimal (hence NIP). One might wonder what other field theories could be present under this banner—and there is a conjecture of Shelah that would answer this question:
Conjecture (Shelah/NIP Fields)
Every infinite NIP field is either separably closed, real closed, or admits a nontrivial henselian valuation.
Theorem 3.11. Assume the NIP Fields Conjecture. Then every infinite NIP field is either real closed, separably closed, or admits a nontrivial henselian valuation
![]() $\emptyset $
-definable in the language of rings.
$\emptyset $
-definable in the language of rings.
Proof (Here a valuation is definable if the valuation ring is a definable subset of the field.)
![]() $\mathcal {L}_r$
-definability is [Reference Halevi, Hasson and Jahnke17, Proposition 6.2(2)], and the results cited in the proof (from [Reference Jahnke and Koenigsmann21]) in fact conclude
$\mathcal {L}_r$
-definability is [Reference Halevi, Hasson and Jahnke17, Proposition 6.2(2)], and the results cited in the proof (from [Reference Jahnke and Koenigsmann21]) in fact conclude
![]() $\emptyset $
-definability.
$\emptyset $
-definability.
Therefore a sensible goal would be to prove that every field with a nontrivial
![]() $\emptyset $
-
$\emptyset $
-
![]() $\mathcal {L}_r$
-definable henselian valuation is finitely undecidable. Or more so, that every henselian valued field is finitely undecidable in the language of valued fields
$\mathcal {L}_r$
-definable henselian valuation is finitely undecidable. Or more so, that every henselian valued field is finitely undecidable in the language of valued fields
![]() $\mathcal {L}_{val}$
.
$\mathcal {L}_{val}$
.
4. Equicharacteristic 0 Henselian valued fields
The previous subsection did not address the aspects of Ziegler’s construction relevant to
![]() $\operatorname {\mathbb {Q}}_p$
; these aspects will be seen in this subsection. In this subsection we will consider a pair of valued fields
$\operatorname {\mathbb {Q}}_p$
; these aspects will be seen in this subsection. In this subsection we will consider a pair of valued fields
![]() $(R, v_R)$
,
$(R, v_R)$
,
![]() $(Z, v_Z)$
, and an additional field F, under the following assumptions:
$(Z, v_Z)$
, and an additional field F, under the following assumptions:
Assumption (
 $\otimes $
)
$\otimes $
)
-
(1)
 $R \subseteq F \subseteq Z$
,
$R \subseteq F \subseteq Z$
,
 $v_R = v_Z|_R$
, and
$v_R = v_Z|_R$
, and
 $(Z, v_Z)$
is a henselian immediate extension of
$(Z, v_Z)$
is a henselian immediate extension of
 $(R, v_R)$
.
$(R, v_R)$
. -
(2) R (thence
 $v_R R$
and
$v_R R$
and
 $R v_R$
) is countable, and if
$R v_R$
) is countable, and if
 $\operatorname {\mathrm {char}}(R)> 0$
then R is transcendental over its prime subfield.
$\operatorname {\mathrm {char}}(R)> 0$
then R is transcendental over its prime subfield. -
(3) There are uncountably many elements of Z transcendental over R.
-
(4)
 $F = Z \cap {R(\overline {x})}^s$
, where
$F = Z \cap {R(\overline {x})}^s$
, where
 $R(\overline {x})$
is a purely transcendental, finite transcendence degree extension of R.
$R(\overline {x})$
is a purely transcendental, finite transcendence degree extension of R. -
(5) Let
 $q> \operatorname {\mathrm {char}}(Rv_R)$
be prime
$q> \operatorname {\mathrm {char}}(Rv_R)$
be prime
 $;$
then
$;$
then
 $Z = (Z)^q \cdot F^*$
.
$Z = (Z)^q \cdot F^*$
.
First we will give a concrete example of a pair of valued fields where these assumptions are satisfied. Let k be a field and
![]() $\Gamma $
an ordered abelian group. Consider the multiplicative group of formal monomials
$\Gamma $
an ordered abelian group. Consider the multiplicative group of formal monomials
![]() $\{t^{\gamma } \mbox { : } \gamma \in \Gamma \}$
, where
$\{t^{\gamma } \mbox { : } \gamma \in \Gamma \}$
, where
![]() $t^0 = 1$
and
$t^0 = 1$
and
![]() $t^{\gamma _1} \cdot t^{\gamma _2} = t^{\gamma _1 + \gamma _2}$
. Define
$t^{\gamma _1} \cdot t^{\gamma _2} = t^{\gamma _1 + \gamma _2}$
. Define
![]() $k[\Gamma ]$
to be the set of formal series
$k[\Gamma ]$
to be the set of formal series
![]() $\sum _{\gamma } a_{\gamma } t^{\gamma }$
where
$\sum _{\gamma } a_{\gamma } t^{\gamma }$
where
![]() $a_{\gamma } \in k$
and only finitely many
$a_{\gamma } \in k$
and only finitely many
![]() $a_{\gamma }$
are nonzero. Addition and multiplication are defined by
$a_{\gamma }$
are nonzero. Addition and multiplication are defined by
 $$ \begin{align*} \sum_{\gamma} a_{\gamma} t^{\gamma} + \sum_{\gamma} b_{\gamma} t^{\gamma} &= \sum_{\gamma} (a_{\gamma} + b_{\gamma}) t^{\gamma},\\ \left( \sum_{\gamma} a_{\gamma} t^{\gamma} \right) \cdot \left( \sum_{\gamma} b_{\gamma} t^{\gamma} \right) &= \sum_{\gamma} \left(\sum_{\gamma_1 + \gamma_2 = \gamma} a_{\gamma_1} b_{\gamma_2} \right) t^{\gamma}. \end{align*} $$
$$ \begin{align*} \sum_{\gamma} a_{\gamma} t^{\gamma} + \sum_{\gamma} b_{\gamma} t^{\gamma} &= \sum_{\gamma} (a_{\gamma} + b_{\gamma}) t^{\gamma},\\ \left( \sum_{\gamma} a_{\gamma} t^{\gamma} \right) \cdot \left( \sum_{\gamma} b_{\gamma} t^{\gamma} \right) &= \sum_{\gamma} \left(\sum_{\gamma_1 + \gamma_2 = \gamma} a_{\gamma_1} b_{\gamma_2} \right) t^{\gamma}. \end{align*} $$
These operations are confirmed to be well-defined, and
![]() $k[\Gamma ]$
an integral domain, by [Reference Marker37, Section 2.4]. This domain comes with a natural valuation
$k[\Gamma ]$
an integral domain, by [Reference Marker37, Section 2.4]. This domain comes with a natural valuation
![]() $v_{\Gamma }(\sum _{\gamma } a_{\gamma } t^{\gamma }) \mathrel {\mathop :}= \min \operatorname {\mathrm {supp}}(\sum _{\gamma } a_{\gamma } t^{\gamma })$
. Define
$v_{\Gamma }(\sum _{\gamma } a_{\gamma } t^{\gamma }) \mathrel {\mathop :}= \min \operatorname {\mathrm {supp}}(\sum _{\gamma } a_{\gamma } t^{\gamma })$
. Define
![]() $k(\Gamma )$
to be the fraction field of this valued domain. Further define
$k(\Gamma )$
to be the fraction field of this valued domain. Further define
![]() $k((\Gamma ))$
as the set whose elements are formal series
$k((\Gamma ))$
as the set whose elements are formal series
![]() $\sum _{\gamma } a_{\gamma } t^{\gamma }$
with well-ordered support. By [Reference Marker37, Section 2.4],
$\sum _{\gamma } a_{\gamma } t^{\gamma }$
with well-ordered support. By [Reference Marker37, Section 2.4],
![]() $(k((\Gamma )), v_{\Gamma })$
is a well-defined immediate henselian overfield of
$(k((\Gamma )), v_{\Gamma })$
is a well-defined immediate henselian overfield of
![]() $(k(\Gamma ), v_{\Gamma })$
.
$(k(\Gamma ), v_{\Gamma })$
.
Lemma 4.1. Let
![]() $e \in \operatorname {\mathbb {N}}$
, k, and
$e \in \operatorname {\mathbb {N}}$
, k, and
![]() $\Gamma $
be countable, and v be a henselian valuation on
$\Gamma $
be countable, and v be a henselian valuation on
![]() $k((\Gamma ))$
which factors through
$k((\Gamma ))$
which factors through
![]() $v_{\Gamma }$
, i.e., there exists a valuation
$v_{\Gamma }$
, i.e., there exists a valuation
![]() $v'$
on k such thatFootnote
4
$v'$
on k such thatFootnote
4
![]() $v = v' \circ v_{\Gamma }$
. There exists
$v = v' \circ v_{\Gamma }$
. There exists
![]() $t_1, \dots , t_e \in k((\Gamma ))$
transcendental over
$t_1, \dots , t_e \in k((\Gamma ))$
transcendental over
![]() $k(\Gamma )$
and algebraically independent such that the pair of valued fields
$k(\Gamma )$
and algebraically independent such that the pair of valued fields
![]() $(R, v_R) = (k(\Gamma ), v|_{k(\Gamma )})$
,
$(R, v_R) = (k(\Gamma ), v|_{k(\Gamma )})$
,
![]() $(Z, v_Z) = (k((\Gamma )), v)$
, and
$(Z, v_Z) = (k((\Gamma )), v)$
, and
![]() $F = k((\Gamma )) \cap \left (k(\Gamma )(t_1, \dots , t_e)\right )^s$
satisfy Assumption
$F = k((\Gamma )) \cap \left (k(\Gamma )(t_1, \dots , t_e)\right )^s$
satisfy Assumption
![]() $(\otimes )$
.
$(\otimes )$
.
Proof Properties (1) and (4) follow by definition. Property (2) follows by construction, and as
![]() $k(\Gamma )$
is countable (from its definition). Property (3) can be seen by a cardinality argument (cf. [Reference van den Dries, Macpherson and Toffalori12, p. 82]): fixing
$k(\Gamma )$
is countable (from its definition). Property (3) can be seen by a cardinality argument (cf. [Reference van den Dries, Macpherson and Toffalori12, p. 82]): fixing
![]() $\gamma \in \Gamma ^{>0}$
, there is an injection
$\gamma \in \Gamma ^{>0}$
, there is an injection
![]() $(\operatorname {\mathbb {N}}; 0, +, <) \hookrightarrow (\Gamma; 0, +, <)$
given by
$(\operatorname {\mathbb {N}}; 0, +, <) \hookrightarrow (\Gamma; 0, +, <)$
given by
![]() $n \mapsto n \cdot \gamma $
, and by definition
$n \mapsto n \cdot \gamma $
, and by definition
![]() $|k((\Gamma ))| \geq |k|^{\aleph _0} \cdot 2^{\aleph _0} = 2^{\aleph _0}$
, while
$|k((\Gamma ))| \geq |k|^{\aleph _0} \cdot 2^{\aleph _0} = 2^{\aleph _0}$
, while
![]() $|\widetilde {k(\Gamma )}| = \aleph _0$
.
$|\widetilde {k(\Gamma )}| = \aleph _0$
.
Property (5) requires more work: we adapt [Reference Ziegler49, Lemma 3]. Clearly
![]() $(k((\Gamma )))^q \cdot F^* \subseteq k((\Gamma ))$
; we are required to show that for all
$(k((\Gamma )))^q \cdot F^* \subseteq k((\Gamma ))$
; we are required to show that for all
![]() $a \in k((\Gamma ))^*$
, there exists
$a \in k((\Gamma ))^*$
, there exists
![]() $b \in F^*$
such that
$b \in F^*$
such that
![]() $a b^{-1} \in (k((\Gamma )))^q$
. Choose
$a b^{-1} \in (k((\Gamma )))^q$
. Choose
![]() $b \in F^*$
such that
$b \in F^*$
such that
![]() $v_{\Gamma }(a - b)> v_{\Gamma }(a)$
; this can be done by setting
$v_{\Gamma }(a - b)> v_{\Gamma }(a)$
; this can be done by setting
![]() $b \in k(\Gamma )^* \subseteq F^*$
to be a sufficiently large finite truncation of a. Then
$b \in k(\Gamma )^* \subseteq F^*$
to be a sufficiently large finite truncation of a. Then
![]() $v_{\Gamma }(a b^{-1} - 1)> v_{\Gamma }(a b^{-1})$
; hence
$v_{\Gamma }(a b^{-1} - 1)> v_{\Gamma }(a b^{-1})$
; hence
![]() $ab^{-1} \equiv 1$
mod
$ab^{-1} \equiv 1$
mod
![]() $\mathfrak {m}_{v_{\Gamma }}$
. By Hensel’s Lemma (regardless of v,
$\mathfrak {m}_{v_{\Gamma }}$
. By Hensel’s Lemma (regardless of v,
![]() $(k((\Gamma )), v_{\Gamma })$
is henselian),
$(k((\Gamma )), v_{\Gamma })$
is henselian),
![]() $ab^{-1}$
is a q-th power in
$ab^{-1}$
is a q-th power in
![]() $k((\Gamma ))$
, as desired.
$k((\Gamma ))$
, as desired.
Using Assumption
![]() $(\otimes )$
, for
$(\otimes )$
, for
![]() $q> p$
prime, we shall construct a field extension
$q> p$
prime, we shall construct a field extension
![]() $F \subseteq K_q \subseteq Z$
such that
$F \subseteq K_q \subseteq Z$
such that
![]() $\operatorname {\mathbb {Z}}$
or
$\operatorname {\mathbb {Z}}$
or
![]() $\mathbb {F}_p[z]$
(where
$\mathbb {F}_p[z]$
(where
![]() $p = \operatorname {\mathrm {char}}(R)> 0$
and
$p = \operatorname {\mathrm {char}}(R)> 0$
and
![]() $z \in Z$
is transcendental over
$z \in Z$
is transcendental over
![]() $\mathbb {F}_p$
) is
$\mathbb {F}_p$
) is
![]() $\mathcal {L}_{val}$
-definable in
$\mathcal {L}_{val}$
-definable in
![]() $K_q$
, and for some elements
$K_q$
, and for some elements
![]() $a \in Z$
algebraic over
$a \in Z$
algebraic over
![]() $K_q$
,
$K_q$
,
![]() $q|[K_q(a) : K_q]$
.
$q|[K_q(a) : K_q]$
.
Remark 4.2. Notice that if Z is perfect, and for all
![]() $a \in Z$
algebraic over
$a \in Z$
algebraic over
![]() $K_q$
we have either
$K_q$
we have either
![]() $K_q(a) = K_q$
or
$K_q(a) = K_q$
or
![]() $q | [K_q(a) : K_q]$
, then
$q | [K_q(a) : K_q]$
, then
![]() $K_q$
is perfect:
$K_q$
is perfect:
![]() $(K_q)^p = K_q$
. This will be a problem for Theorem 5.8
, where we will consider finite subtheories T of imperfect fields and prove
$(K_q)^p = K_q$
. This will be a problem for Theorem 5.8
, where we will consider finite subtheories T of imperfect fields and prove
![]() $K_q \models T$
. This problem will be resolved after Lemma 4.3
.
$K_q \models T$
. This problem will be resolved after Lemma 4.3
.
By Assumption
![]() $(\otimes )$
there exists an element
$(\otimes )$
there exists an element
![]() $t \in Z$
transcendental over F. The field
$t \in Z$
transcendental over F. The field
![]() $K_q$
will be the union of a specific sequence of finite extensions of
$K_q$
will be the union of a specific sequence of finite extensions of
![]() $F(t)$
in Z:
$F(t)$
in Z:
As before, we will also construct a sequence
![]() $\emptyset = S_0 \subseteq S_1 \subseteq S_2 \subseteq \cdots $
of finite subsets
$\emptyset = S_0 \subseteq S_1 \subseteq S_2 \subseteq \cdots $
of finite subsets
![]() $S_i \subseteq E_i \cap (Z)^q$
, ultimately desiring a close relationship between
$S_i \subseteq E_i \cap (Z)^q$
, ultimately desiring a close relationship between
![]() $K_q \setminus (F^* \cdot (K_q)^q)$
,
$K_q \setminus (F^* \cdot (K_q)^q)$
,
![]() $(K_q \cap (Z)^q) \setminus (K_q)^q$
, and
$(K_q \cap (Z)^q) \setminus (K_q)^q$
, and
![]() $\bigcup _i S_i$
. We will desire F &
$\bigcup _i S_i$
. We will desire F &
![]() $\operatorname {\mathbb {Z}}$
(if
$\operatorname {\mathbb {Z}}$
(if
![]() $\operatorname {\mathrm {char}}(R) = 0$
;
$\operatorname {\mathrm {char}}(R) = 0$
;
![]() $\mathbb {F}_p[z]$
otherwise) to have the following definitions, similar to as before:
$\mathbb {F}_p[z]$
otherwise) to have the following definitions, similar to as before:
 $$ \begin{align*} &F = \{ a \in K_q \mbox{ : }\forall b \in K_q \cap (Z)^q\setminus\{0\} \mbox{, } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q] \rightarrow b \in (K_q)^q)\},\\&\operatorname{\mathbb{Z}} \mbox{ (resp.\!}\ \mathbb{F}_p[z] = \{u \in F \mbox{ : } \forall u_1 \neq u_2 \in F \mbox{ s.t. } u_1 + u_2 = u\mbox{, } t^q - u_1 \mbox{ or } t^q - u_2 \in (K_q)^q\}. \end{align*} $$
$$ \begin{align*} &F = \{ a \in K_q \mbox{ : }\forall b \in K_q \cap (Z)^q\setminus\{0\} \mbox{, } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q] \rightarrow b \in (K_q)^q)\},\\&\operatorname{\mathbb{Z}} \mbox{ (resp.\!}\ \mathbb{F}_p[z] = \{u \in F \mbox{ : } \forall u_1 \neq u_2 \in F \mbox{ s.t. } u_1 + u_2 = u\mbox{, } t^q - u_1 \mbox{ or } t^q - u_2 \in (K_q)^q\}. \end{align*} $$
Denote by “
![]() $v_Z|_{E_i}$
” the restriction of
$v_Z|_{E_i}$
” the restriction of
![]() $v_Z$
to
$v_Z$
to
![]() $E_i \subseteq Z$
. To again ensure we do not introduce an incompatibility between
$E_i \subseteq Z$
. To again ensure we do not introduce an incompatibility between
![]() $(K_q \cap (Z)^q) \setminus (K_q)^q$
and F or
$(K_q \cap (Z)^q) \setminus (K_q)^q$
and F or
![]() $\operatorname {\mathbb {Z}}$
(resp.
$\operatorname {\mathbb {Z}}$
(resp.
![]() $\mathbb {F}_p[z]$
), the following rule will be enforced during the construction:
$\mathbb {F}_p[z]$
), the following rule will be enforced during the construction:
 $$ \begin{align} & \mbox{There is a family of discrete valuations}\ \{v_s\}_{s \in S_i}\ \text{on}\ E_i\ \text{such that}\ v_s(F) = 0 \nonumber\\& \mbox{and}\ q \nmid v_s(s)\ \text{for}\ s \in S_i.\ \text{In addition, for all}\ u_1 \neq u_2 \in F\ \text{with}\ u_1 + u_2 \in \operatorname{\mathbb{Z}} \\& \mbox{(resp.}\!\ \mathbb{F}_p[z]),\ \text{either}\ \forall s \in S_i,\ q | v_s(t^q - u_1),\ \text{or}\ \forall s \in S_i,\ q | v_s(t^q - u_2). \nonumber \end{align} $$
$$ \begin{align} & \mbox{There is a family of discrete valuations}\ \{v_s\}_{s \in S_i}\ \text{on}\ E_i\ \text{such that}\ v_s(F) = 0 \nonumber\\& \mbox{and}\ q \nmid v_s(s)\ \text{for}\ s \in S_i.\ \text{In addition, for all}\ u_1 \neq u_2 \in F\ \text{with}\ u_1 + u_2 \in \operatorname{\mathbb{Z}} \\& \mbox{(resp.}\!\ \mathbb{F}_p[z]),\ \text{either}\ \forall s \in S_i,\ q | v_s(t^q - u_1),\ \text{or}\ \forall s \in S_i,\ q | v_s(t^q - u_2). \nonumber \end{align} $$
We have the following lemma:
Lemma 4.3. Let u be a nontrivial discrete valuation on
![]() $E_i$
, considered as a (finite) function field extension of
$E_i$
, considered as a (finite) function field extension of
![]() $F(t)/F$
. Then u and
$F(t)/F$
. Then u and
![]() $v_Z|_{E_i}$
are independent (in the sense of Definition 3.4).
$v_Z|_{E_i}$
are independent (in the sense of Definition 3.4).
Proof Assume u and
![]() $v_Z|_{E_i}$
are dependent: by [Reference Engler and Prestel13, Theorem 2.3.4] they induce the same topology on
$v_Z|_{E_i}$
are dependent: by [Reference Engler and Prestel13, Theorem 2.3.4] they induce the same topology on
![]() $E_i$
. Thus there exists
$E_i$
. Thus there exists
![]() $a \in E_i$
such that
$a \in E_i$
such that
![]() $a \cdot \mathfrak {m}_{u} \subseteq \mathfrak {m}_{v_Z|_{E_i}}$
(
$a \cdot \mathfrak {m}_{u} \subseteq \mathfrak {m}_{v_Z|_{E_i}}$
(
![]() $= \mathfrak {m}_{v_Z} \cap E_i$
). However, as R is a subset of the constant subfield of
$= \mathfrak {m}_{v_Z} \cap E_i$
). However, as R is a subset of the constant subfield of
![]() $E_i$
(and thus
$E_i$
(and thus
![]() $u(R) = 0$
, while
$u(R) = 0$
, while
![]() $v_R R = v_Z Z$
), there exists
$v_R R = v_Z Z$
), there exists
![]() $f \in a \cdot \mathfrak {m}_u$
with
$f \in a \cdot \mathfrak {m}_u$
with
![]() $v_Z(f) = v_Z|_{E_i}(f) < 0$
; a contradiction.
$v_Z(f) = v_Z|_{E_i}(f) < 0$
; a contradiction.
To use the same construction of
![]() $K_q$
throughout the paper, yet have
$K_q$
throughout the paper, yet have
![]() $K_q$
a model of a finite subtheory of either a perfect or imperfect field, we have the following definition:
$K_q$
a model of a finite subtheory of either a perfect or imperfect field, we have the following definition:
Definition 4.4. The set of pliant elements over a field will denote either the separably algebraic or algebraic elements over the field, and be specified in Corollary 4.10/Theorem 5.3/Theorem 5.8.
Fix an enumeration
![]() $a_0, a_1, \dots $
of the elements of Z pliant over
$a_0, a_1, \dots $
of the elements of Z pliant over
![]() $F(t)$
, each repeated countably infinitely many times. Suppose
$F(t)$
, each repeated countably infinitely many times. Suppose
![]() $(E_i, S_i)$
is already constructed—and consider the following modified construction.
$(E_i, S_i)$
is already constructed—and consider the following modified construction.
Modified Construction.
Case 1:
![]() $i = 4n$
. As on page 6.
$i = 4n$
. As on page 6.
Case 2:
![]() $i = 4n + 1$
. If
$i = 4n + 1$
. If
![]() $a_n \not \in E_i$
or
$a_n \not \in E_i$
or
![]() $a_n \not \in (Z)^q$
then set
$a_n \not \in (Z)^q$
then set
![]() $(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise proceed as on page 6.
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise proceed as on page 6.
Case 3:
![]() $i = 4n+2$
. Unless
$i = 4n+2$
. Unless
![]() $a_n \in E_i \setminus F$
, let
$a_n \in E_i \setminus F$
, let
![]() $(E_{i+1}, S_{i+1})= (E_i, S_i)$
. If
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. If
![]() $a_n \in E_i \setminus F$
let w be a discrete valuation on
$a_n \in E_i \setminus F$
let w be a discrete valuation on
![]() $E_i$
(considered as a function field extension of
$E_i$
(considered as a function field extension of
![]() $F(t)/F$
), trivial on F, which is negative on
$F(t)/F$
), trivial on F, which is negative on
![]() $a_n$
. By Lemma 4.3
, w and
$a_n$
. By Lemma 4.3
, w and
![]() $v_Z|_{E_i}$
are independent. Let us define a finite separable extension
$v_Z|_{E_i}$
are independent. Let us define a finite separable extension
![]() $E/E_i$
: if the second condition of (
$E/E_i$
: if the second condition of (![]() ) already holds for
) already holds for
![]() $\{w, \{v_s\}_{s \in S_i}\}$
in
$\{w, \{v_s\}_{s \in S_i}\}$
in
![]() $E_i$
, set
$E_i$
, set
![]() $E = E_i$
. Otherwise there exists
$E = E_i$
. Otherwise there exists
![]() $u \in F$
such that
$u \in F$
such that
![]() $q \nmid w(t^q - u)$
and
$q \nmid w(t^q - u)$
and
![]() $q | v_s(t^q - u)$
for all
$q | v_s(t^q - u)$
for all
![]() $s \in S_i$
. By the strong triangle inequality, there is at most one such u.
$s \in S_i$
. By the strong triangle inequality, there is at most one such u.
Under Assumption
![]() $(\otimes )(5)$
there exists
$(\otimes )(5)$
there exists
![]() $d \in F^*$
such that
$d \in F^*$
such that
![]() $d(t^q - u) \in (Z)^q$
. Thus we may set
$d(t^q - u) \in (Z)^q$
. Thus we may set
![]() $E = E_i(\sqrt [q]{d(t^q - u)})$
and extend the valuations
$E = E_i(\sqrt [q]{d(t^q - u)})$
and extend the valuations
![]() $\{v_s\}_{s \in S_i}$
sensibly as before (and let
$\{v_s\}_{s \in S_i}$
sensibly as before (and let
![]() $w'$
be any extension to E of w). We conclude the second condition of (
$w'$
be any extension to E of w). We conclude the second condition of (![]() ) now holds for
) now holds for
![]() $(E, \{w', \{v_s\}_{s \in S_i}\})$
.
$(E, \{w', \{v_s\}_{s \in S_i}\})$
.
If
![]() $w'$
is independent to
$w'$
is independent to
![]() $v_s$
for every
$v_s$
for every
![]() $s \in S_i$
: let
$s \in S_i$
: let
![]() $\{w', v_{s_1}, \dots , v_{s_k}\}$
be the distinct valuations of
$\{w', v_{s_1}, \dots , v_{s_k}\}$
be the distinct valuations of
![]() $\{w', \{v_s\}_{s \in S_i}\}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
$\{w', \{v_s\}_{s \in S_i}\}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
![]() $b \in E$
such that
$b \in E$
such that
![]() $w'(b)$
is the smallest positive element of its value group,
$w'(b)$
is the smallest positive element of its value group,
![]() $q | v_{s_j}(b)$
and
$q | v_{s_j}(b)$
and
![]() $v_{s_j}(b) < 0, -v_{s_j}(a_n^q)$
for
$v_{s_j}(b) < 0, -v_{s_j}(a_n^q)$
for
![]() $1 \leq j \leq k$
. Notice
$1 \leq j \leq k$
. Notice
![]() $q | w'(1+b)$
,
$q | w'(1+b)$
,
![]() $q|w'(a_n^q + b^{-1})$
, and
$q|w'(a_n^q + b^{-1})$
, and
![]() $q|v_s(a_n^q + b^{-1})$
,
$q|v_s(a_n^q + b^{-1})$
,
![]() $q|v_s(1+b)$
for all
$q|v_s(1+b)$
for all
![]() $s \in S_i$
.
$s \in S_i$
.
We also wish
![]() $b, 1+b, a_n^q + b^{-1} \in (Z)^q$
. This can be achieved with further care by using the Approximation Theorem and Hensel’s Lemma: by Lemma 4.3
and [Reference Engler and Prestel13, Corollary 2.3.2],
$b, 1+b, a_n^q + b^{-1} \in (Z)^q$
. This can be achieved with further care by using the Approximation Theorem and Hensel’s Lemma: by Lemma 4.3
and [Reference Engler and Prestel13, Corollary 2.3.2],
![]() $v_Z|_{E}$
,
$v_Z|_{E}$
,
![]() $w'$
, and
$w'$
, and
![]() $v_{s_j}$
for
$v_{s_j}$
for
![]() $1 \leq j \leq k$
are pairwise independent. Let
$1 \leq j \leq k$
are pairwise independent. Let
![]() $d \in (E)^q \subseteq (Z)^q$
have
$d \in (E)^q \subseteq (Z)^q$
have
![]() $v_Z|_E(d)> 0$
. Using the Approximation Theorem, we choose
$v_Z|_E(d)> 0$
. Using the Approximation Theorem, we choose
![]() $b \in E$
so that in addition
$b \in E$
so that in addition
![]() $v_Z|_E(b - d)> v_Z|_E(d)$
. Then by Hensel’s Lemma,
$v_Z|_E(b - d)> v_Z|_E(d)$
. Then by Hensel’s Lemma,
![]() $b \in E \cap (Z)^q$
, and since
$b \in E \cap (Z)^q$
, and since
![]() $v_Z|_E((b+1) - 1) = v_Z|_E(b)$
and
$v_Z|_E((b+1) - 1) = v_Z|_E(b)$
and
![]() $v_Z|_E((b + a_n^{-q}) - a_n^{-q}) = v_Z|_E(b)$
, we have
$v_Z|_E((b + a_n^{-q}) - a_n^{-q}) = v_Z|_E(b)$
, we have
![]() $1 + b, b + a_n^{-q} \in E \cap (Z)^q$
. (Hence
$1 + b, b + a_n^{-q} \in E \cap (Z)^q$
. (Hence
![]() $a_n^q + b^{-1} \in E \cap (Z)^q$
.) We define
$a_n^q + b^{-1} \in E \cap (Z)^q$
.) We define
Extending
![]() $\{v_b = w', \{v_s\}_{s \in S_i}\}$
as in Case 2, (
$\{v_b = w', \{v_s\}_{s \in S_i}\}$
as in Case 2, (![]() ) holds as it did on E.
) holds as it did on E.
Now assume
![]() $w'$
is dependent with
$w'$
is dependent with
![]() $v_{\widehat {s}}$
for some
$v_{\widehat {s}}$
for some
![]() $\widehat {s} \in S_i$
: in which case,
$\widehat {s} \in S_i$
: in which case,
![]() $w' = v_{\widehat {s}}$
by Lemma 3.5
. Let
$w' = v_{\widehat {s}}$
by Lemma 3.5
. Let
![]() $\{v_{s_1}, \dots , v_{s_l}\}$
be the distinct valuations of
$\{v_{s_1}, \dots , v_{s_l}\}$
be the distinct valuations of
![]() $\{w', \{v_s\}_{s \in S_i}\}$
, assuming WLOG
$\{w', \{v_s\}_{s \in S_i}\}$
, assuming WLOG
![]() $w' = v_{s_1}$
. By Lemma 4.3
and [Reference Engler and Prestel13, Corollary 2.3.2],
$w' = v_{s_1}$
. By Lemma 4.3
and [Reference Engler and Prestel13, Corollary 2.3.2],
![]() $v_Z|_{E}$
, and
$v_Z|_{E}$
, and
![]() $v_{s_j}$
for
$v_{s_j}$
for
![]() $1 \leq j \leq l$
are pairwise independent. Let
$1 \leq j \leq l$
are pairwise independent. Let
![]() $d \in (E)^q \subseteq (Z)^q$
have
$d \in (E)^q \subseteq (Z)^q$
have
![]() $v_Z|_E(d)> 0$
. Using the Approximation Theorem, we choose
$v_Z|_E(d)> 0$
. Using the Approximation Theorem, we choose
![]() $b \in E$
so that
$b \in E$
so that
![]() $v_Z|_E(b - d)> v_Z|_E(d)$
,
$v_Z|_E(b - d)> v_Z|_E(d)$
,
![]() $v_{s_1}(b)$
is the smallest positive element of its value group,
$v_{s_1}(b)$
is the smallest positive element of its value group,
![]() $q | v_{s_j}(b)$
and
$q | v_{s_j}(b)$
and
![]() $v_{s_j}(b) < 0, -v_{s_j}(a_n^q)$
for
$v_{s_j}(b) < 0, -v_{s_j}(a_n^q)$
for
![]() $2 \leq j \leq l$
. By Hensel’s Lemma,
$2 \leq j \leq l$
. By Hensel’s Lemma,
![]() $1 + b, a_n^q + b^{-1} \in E \cap (Z)^q$
, and we may define
$1 + b, a_n^q + b^{-1} \in E \cap (Z)^q$
, and we may define
Extending
![]() $\{v_b = w', \{v_s\}_{s \in S_i}\}$
as in Case 2, (
$\{v_b = w', \{v_s\}_{s \in S_i}\}$
as in Case 2, (![]() ) holds on
) holds on
![]() $(E_{i+1}, S_{i+1})$
. (Again this case allows for
$(E_{i+1}, S_{i+1})$
. (Again this case allows for
![]() $b \in S_i$
without issue, by Lemma 3.5
.)
$b \in S_i$
without issue, by Lemma 3.5
.)
Case 4:
![]() $i = 4n +3$
. As on page 6. Recall this step extends
$i = 4n +3$
. As on page 6. Recall this step extends
![]() $\{v_s\}_{s \in S_i}$
to
$\{v_s\}_{s \in S_i}$
to
![]() $\{v_s\}_{s\in S_{i+1}} = \{w_{r_1}, w_{r_2}, \{v_s\}_{s \in S_i}\}$
. The valuations
$\{v_s\}_{s\in S_{i+1}} = \{w_{r_1}, w_{r_2}, \{v_s\}_{s \in S_i}\}$
. The valuations
![]() $w_{r_1}, w_{r_2}$
are independent to
$w_{r_1}, w_{r_2}$
are independent to
![]() $v_Z|_{E_i}$
by Lemma 4.3
, and (
$v_Z|_{E_i}$
by Lemma 4.3
, and (![]() ) is satisfied.⊣
) is satisfied.⊣
Now we can show the following (cf. Lemma 3.6 ):
Lemma 4.5. Set
![]() $K_q = \bigcup _i E_i$
. The above construction ensures we have the following features of
$K_q = \bigcup _i E_i$
. The above construction ensures we have the following features of
![]() $K_q$
under Assumption
$K_q$
under Assumption
![]() $(\otimes )$
:
$(\otimes )$
:
-
(1)
 $(K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
.
$(K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
. -
(2)
 $F^* \cdot \left ( \bigcup _i S_i \right ) = K_q \setminus (F^* \cdot (K_q)^q)$
.
$F^* \cdot \left ( \bigcup _i S_i \right ) = K_q \setminus (F^* \cdot (K_q)^q)$
. -
(3)
 $F \!=\! \{ a \in {K_q}\!:\!\forall b \in K_q \cap (Z)^q\setminus \{0\} \mbox { } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q]\! \rightarrow \! b \in (K_q)^q)\}$
.
$F \!=\! \{ a \in {K_q}\!:\!\forall b \in K_q \cap (Z)^q\setminus \{0\} \mbox { } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q]\! \rightarrow \! b \in (K_q)^q)\}$
. -
(4)
 $\operatorname {\mathbb {Z}} \mbox{(resp.}\ \mathbb{F}_p[z]) = \{u \in F : \forall u_1 \neq u_2 \in F \mbox { s.t. } u_1 + u_2 = u\mbox {, } t^q - u_1 \mbox { or } t^q - u_2 \in F^* \cdot (K_q)^q\}$
.
$\operatorname {\mathbb {Z}} \mbox{(resp.}\ \mathbb{F}_p[z]) = \{u \in F : \forall u_1 \neq u_2 \in F \mbox { s.t. } u_1 + u_2 = u\mbox {, } t^q - u_1 \mbox { or } t^q - u_2 \in F^* \cdot (K_q)^q\}$
.
Proof In [Reference Ziegler49, Section 4], but for exposition:
-
(1) Let
 $a \in (K_q \cap (Z)^q)\setminus (K_q)^q$
. For some n sufficiently large,
$a \in (K_q \cap (Z)^q)\setminus (K_q)^q$
. For some n sufficiently large,
 $a_n = a$
and
$a_n = a$
and
 $a_n \in E_{4n+1}$
. Case 2 of the above construction assures
$a_n \in E_{4n+1}$
. Case 2 of the above construction assures
 $a_n \in S_{4n+2}$
, hence
$a_n \in S_{4n+2}$
, hence
 $a \in \bigcup _i S_i$
as desired. Conversely, by construction
$a \in \bigcup _i S_i$
as desired. Conversely, by construction
 $\bigcup _i S_i \subseteq K_q \cap (Z)^q$
, and
$\bigcup _i S_i \subseteq K_q \cap (Z)^q$
, and
 $S_i \cap (K_q)^q = \emptyset $
for all i.
$S_i \cap (K_q)^q = \emptyset $
for all i. -
(2) Let
 $a \in F^* \cdot (K_q)^q$
. For all i sufficiently large,
$a \in F^* \cdot (K_q)^q$
. For all i sufficiently large,
 $a \in F^* \cdot (E_i)^q$
and hence
$a \in F^* \cdot (E_i)^q$
and hence
 $q|u(a)$
for all valuations u trivial on F. By design of (
$q|u(a)$
for all valuations u trivial on F. By design of ( ),
),
 $a \not \in F^* \cdot S_i$
, hence
$a \not \in F^* \cdot S_i$
, hence
 $F^* \cdot \left ( \bigcup _i S_i \right ) \subseteq K_q \setminus (F^* \cdot (K_q)^q)$
. Conversely, if
$F^* \cdot \left ( \bigcup _i S_i \right ) \subseteq K_q \setminus (F^* \cdot (K_q)^q)$
. Conversely, if
 $a \in K_q \setminus (F^* \cdot (K_q)^q)$
, then by Assumption
$a \in K_q \setminus (F^* \cdot (K_q)^q)$
, then by Assumption
 $(\otimes )(5)$
there exists
$(\otimes )(5)$
there exists
 $b \in F^*$
with
$b \in F^*$
with
 $ab \in (K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
by (1).
$ab \in (K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
by (1). -
(3) Let
 $a \in F$
. Suppose for
$a \in F$
. Suppose for
 $b \in {K_q} \cap (Z)^q \setminus \{0\}$
, we have
$b \in {K_q} \cap (Z)^q \setminus \{0\}$
, we have
 $1 + b, a^q + b^{-1} \in (K_q)^q$
. Let i be sufficiently large such that
$1 + b, a^q + b^{-1} \in (K_q)^q$
. Let i be sufficiently large such that
 $1 + b, a^q + b^{-1} \in (E_i)^q$
. Notice that, for any valuation u on
$1 + b, a^q + b^{-1} \in (E_i)^q$
. Notice that, for any valuation u on
 $E_i$
trivial on F,
$E_i$
trivial on F,
 $q|u(b)$
: indeed, if
$q|u(b)$
: indeed, if
 $u(b) < 0$
then
$u(b) < 0$
then
 $u(b) = u(1 + b)$
, and if
$u(b) = u(1 + b)$
, and if
 $u(b)> 0$
then
$u(b)> 0$
then
 $u(b) = u(a^q + b^{-1})$
. By (
$u(b) = u(a^q + b^{-1})$
. By ( )
)
 $b \not \in S_i$
(for all subsequent i too), hence as
$b \not \in S_i$
(for all subsequent i too), hence as
 $b \in K_q \cap (Z)^q$
,
$b \in K_q \cap (Z)^q$
,
 $b \in (K_q)^q$
by (1).
$b \in (K_q)^q$
by (1).Conversely, if
 $a \in K_q \setminus F$
, then for some n sufficiently large we may assume
$a \in K_q \setminus F$
, then for some n sufficiently large we may assume
 $a_n = a$
and
$a_n = a$
and
 $a \in E_{4n+2}$
. By Case 3 of the construction, there exists
$a \in E_{4n+2}$
. By Case 3 of the construction, there exists
 $b \in S_{4n+3}$
such that
$b \in S_{4n+3}$
such that
 $1+ b, a^q + b^{-1} \in (E_{4n+3})^q$
and
$1+ b, a^q + b^{-1} \in (E_{4n+3})^q$
and
 $b \in K_q \cap (Z)^q$
. Therefore by (1), as desired.
$b \in K_q \cap (Z)^q$
. Therefore by (1), as desired. $$\begin{align*}\exists b \in K_q \cap (Z)^q\setminus\{0\} \mbox{, }(1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q \land b \not\in (K_q)^q),\end{align*}$$
$$\begin{align*}\exists b \in K_q \cap (Z)^q\setminus\{0\} \mbox{, }(1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q \land b \not\in (K_q)^q),\end{align*}$$
-
(4) Let
 $u \in \operatorname {\mathbb {Z}}$
(resp.
$u \in \operatorname {\mathbb {Z}}$
(resp.
 $\mathbb {F}_p[z]$
),
$\mathbb {F}_p[z]$
),
 $u_1 \neq u_2 \in F$
, and
$u_1 \neq u_2 \in F$
, and
 $u_1 + u_2 = u$
. Assume for the purpose of contradiction both
$u_1 + u_2 = u$
. Assume for the purpose of contradiction both
 $t^q - u_1, t^q - u_2 \not \in F^* \cdot (K_q)^q$
. By the argument in Case 4 there exist
$t^q - u_1, t^q - u_2 \not \in F^* \cdot (K_q)^q$
. By the argument in Case 4 there exist
 $d_1, d_2$
such that
$d_1, d_2$
such that
 $d_1(t^q - u_1), d_2(t^q - u_2) \in (K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
, by (1). We conclude for some sufficiently large i that
$d_1(t^q - u_1), d_2(t^q - u_2) \in (K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
, by (1). We conclude for some sufficiently large i that
 $t^q - u_1, t^q - u_2 \in F^* \cdot S_i$
, contradicting (
$t^q - u_1, t^q - u_2 \in F^* \cdot S_i$
, contradicting ( ).
).Conversely, if
 $u \in F \setminus \operatorname {\mathbb {Z}}$
(resp.
$u \in F \setminus \operatorname {\mathbb {Z}}$
(resp.
 $F \setminus \mathbb {F}_{p}[z]$
), then for some n sufficiently large we may assume
$F \setminus \mathbb {F}_{p}[z]$
), then for some n sufficiently large we may assume
 $a_n = u$
and
$a_n = u$
and
 $a_n \in E_{4n+3}$
. By Case 3 of the construction, deliberately there exists
$a_n \in E_{4n+3}$
. By Case 3 of the construction, deliberately there exists
 $u_1 \neq u_2 \in F^*$
with
$u_1 \neq u_2 \in F^*$
with
 $u_1 + u_2 = u$
and
$u_1 + u_2 = u$
and
 $t^q - u_1, t^q - u_2 \in S_{4n+4} \subseteq F^* \cdot S_{4n+4}$
. Therefore by (2),
$t^q - u_1, t^q - u_2 \in S_{4n+4} \subseteq F^* \cdot S_{4n+4}$
. Therefore by (2),
 $t^q - u_1, t^q - u_2 \not \in F^* \cdot (K_q)^q$
as required for this argument.
$t^q - u_1, t^q - u_2 \not \in F^* \cdot (K_q)^q$
as required for this argument.
Let us return to the case
![]() $(R, v_R) = (k(\Gamma ), v|_{k(\Gamma )})$
,
$(R, v_R) = (k(\Gamma ), v|_{k(\Gamma )})$
,
![]() $(Z, v_Z) = (k((\Gamma )), v)$
,
$(Z, v_Z) = (k((\Gamma )), v)$
,
![]() $F = k((\Gamma )) \cap \left ({k(\Gamma )(t_1, \dots , t_e)}\right )^s$
. We have the following additional results:
$F = k((\Gamma )) \cap \left ({k(\Gamma )(t_1, \dots , t_e)}\right )^s$
. We have the following additional results:
Theorem 4.6 ((Ax–Kochen–Ershov) [Reference Ax and Kochen3, Reference Ershov14])
Let
![]() $(K, v)$
,
$(K, v)$
,
![]() $(L, w)$
be equicharacteristic
$(L, w)$
be equicharacteristic
![]() $0$
henselian valued fields. Then
$0$
henselian valued fields. Then
![]() $K \equiv _{\mathcal {L}_{val}} L$
if and only if
$K \equiv _{\mathcal {L}_{val}} L$
if and only if
![]() $Kv \equiv _{\mathcal {L}_r} Lw$
and
$Kv \equiv _{\mathcal {L}_r} Lw$
and
![]() $vK \equiv _{\mathcal {L}_{oag}} wL$
.
$vK \equiv _{\mathcal {L}_{oag}} wL$
.
Consequently,
![]() $(K, v) \equiv (Kv((vK)), v_{vK})$
, the field of Hahn series in
$(K, v) \equiv (Kv((vK)), v_{vK})$
, the field of Hahn series in
![]() $vK$
over
$vK$
over
![]() $Kv$
.
$Kv$
.
Lemma 4.7. Let
![]() $q> \operatorname {\mathrm {char}}(k)$
be prime and v a henselian valuation on
$q> \operatorname {\mathrm {char}}(k)$
be prime and v a henselian valuation on
![]() $k((\Gamma ))$
which factors through
$k((\Gamma ))$
which factors through
![]() $v_{\Gamma }$
, where k and
$v_{\Gamma }$
, where k and
![]() $\Gamma $
are countable, and
$\Gamma $
are countable, and
![]() $K_q$
as above. Then
$K_q$
as above. Then
![]() $K_q \cap (k((\Gamma )))^q$
is
$K_q \cap (k((\Gamma )))^q$
is
![]() $\mathcal {L}_{val}$
-definable in
$\mathcal {L}_{val}$
-definable in
![]() $(K_q, w)$
, where
$(K_q, w)$
, where
![]() $w = v|_{K_q}$
.
$w = v|_{K_q}$
.
Proof Recall from Lemma 4.1
that Assumption
![]() $(\otimes )$
is satisfied. It suffices to show
$(\otimes )$
is satisfied. It suffices to show
![]() $c \in K_q \cap (k((\Gamma )))^q$
if and only if there exists
$c \in K_q \cap (k((\Gamma )))^q$
if and only if there exists
![]() $d \in K_q$
such that
$d \in K_q$
such that
![]() $w(c - d^q)> w(c)$
.
$w(c - d^q)> w(c)$
.
Assume there exists
![]() $d \in K_q$
such that
$d \in K_q$
such that
![]() $w(c - d^q)> w(c)$
; then (as elements of
$w(c - d^q)> w(c)$
; then (as elements of
![]() $k((\Gamma ))$
) we have
$k((\Gamma ))$
) we have
![]() $v(c - d^q)> v(c)$
, hence
$v(c - d^q)> v(c)$
, hence
![]() $v(1 - \tfrac {d^q}{c})> 0$
, and thus
$v(1 - \tfrac {d^q}{c})> 0$
, and thus
![]() $1 \equiv {\tfrac {d^q}{c}}$
mod
$1 \equiv {\tfrac {d^q}{c}}$
mod
![]() $\mathfrak {m}_{v}$
. By Hensel’s Lemma, there exists
$\mathfrak {m}_{v}$
. By Hensel’s Lemma, there exists
![]() $e \in k((\Gamma ))$
such that
$e \in k((\Gamma ))$
such that
![]() $e^q = \tfrac {d^q}{c}$
; we conclude
$e^q = \tfrac {d^q}{c}$
; we conclude
![]() $c \in (k((\Gamma )))^q$
.
$c \in (k((\Gamma )))^q$
.
Conversely, let
![]() $c \in K_q \cap (k((\Gamma )))^q$
and write
$c \in K_q \cap (k((\Gamma )))^q$
and write
![]() $c = \widehat {d}^q$
. Let
$c = \widehat {d}^q$
. Let
![]() $d \in k(\Gamma )$
be a sufficiently large finite truncation of
$d \in k(\Gamma )$
be a sufficiently large finite truncation of
![]() $\widehat {d} \in k((\Gamma ))$
such that
$\widehat {d} \in k((\Gamma ))$
such that
![]() $v_{\Gamma }(\widehat {d} - d)> v_{\Gamma }(\widehat {d})$
(and note
$v_{\Gamma }(\widehat {d} - d)> v_{\Gamma }(\widehat {d})$
(and note
![]() $v_{\Gamma }(\widehat {d}) = v_{\Gamma }(d)$
). Then
$v_{\Gamma }(\widehat {d}) = v_{\Gamma }(d)$
). Then
 $$ \begin{align*} v_{\Gamma}(\widehat{d}^q - d^q) &= v_{\Gamma}(\widehat{d} - d) + v_{\Gamma}(\widehat{d}^{q-1} + \widehat{d}^{q-2} d + \dots + \widehat{d} d^{q-2} + d^{q-1})\\ &\geq v_{\Gamma}(\widehat{d} - d) + (q-1) v_{\Gamma}(\widehat{d})> q v_{\Gamma}(\widehat{d}) = v_{\Gamma}(\widehat{d}^q), \quad \mbox{hence}\ v_{\Gamma}(\tfrac{\widehat{d}^q - d^q}{\widehat{d}^q}) > 0. \end{align*} $$
$$ \begin{align*} v_{\Gamma}(\widehat{d}^q - d^q) &= v_{\Gamma}(\widehat{d} - d) + v_{\Gamma}(\widehat{d}^{q-1} + \widehat{d}^{q-2} d + \dots + \widehat{d} d^{q-2} + d^{q-1})\\ &\geq v_{\Gamma}(\widehat{d} - d) + (q-1) v_{\Gamma}(\widehat{d})> q v_{\Gamma}(\widehat{d}) = v_{\Gamma}(\widehat{d}^q), \quad \mbox{hence}\ v_{\Gamma}(\tfrac{\widehat{d}^q - d^q}{\widehat{d}^q}) > 0. \end{align*} $$
Consequently
![]() $v(\tfrac {\widehat {d}^q - d^q}{\widehat {d}^q})> 0$
, i.e.,
$v(\tfrac {\widehat {d}^q - d^q}{\widehat {d}^q})> 0$
, i.e.,
![]() $v(\widehat {d}^q - d^q)> v(\widehat {d}^q)$
; equivalently
$v(\widehat {d}^q - d^q)> v(\widehat {d}^q)$
; equivalently
![]() $v(c - d^q)> v(c)$
and hence
$v(c - d^q)> v(c)$
and hence
![]() $w(c - d^q)> w(c)$
as desired.
$w(c - d^q)> w(c)$
as desired.
Theorem 4.8. Let
![]() $q> \operatorname {\mathrm {char}}(k)$
be prime, v a henselian valuation on
$q> \operatorname {\mathrm {char}}(k)$
be prime, v a henselian valuation on
![]() $k((\Gamma ))$
which factors through
$k((\Gamma ))$
which factors through
![]() $v_{\Gamma }$
, where k and
$v_{\Gamma }$
, where k and
![]() $\Gamma $
are countable, and
$\Gamma $
are countable, and
![]() $K_q$
as above. Then:
$K_q$
as above. Then:
-
(1)
 $(K_q, v_{\Gamma }|_{K_q})$
is an immediate extension of
$(K_q, v_{\Gamma }|_{K_q})$
is an immediate extension of
 $(k(\Gamma ), v_{\Gamma })$
.
$(k(\Gamma ), v_{\Gamma })$
. -
(2)
 $(K_q, v|_{K_q})$
is an immediate extension of
$(K_q, v|_{K_q})$
is an immediate extension of
 $(k(\Gamma ), v)$
.
$(k(\Gamma ), v)$
. -
(3)
 $\operatorname {\mathbb {Z}}$
(resp.
$\operatorname {\mathbb {Z}}$
(resp.
 $\mathbb {F}_p[z])$
is definable in
$\mathbb {F}_p[z])$
is definable in
 $K_q$
in the language
$K_q$
in the language
 $\{0, 1, +, \times , \mathcal {O}_{v|_{K_q}}\}$
.
$\{0, 1, +, \times , \mathcal {O}_{v|_{K_q}}\}$
. -
(4) If
 $a \in k((\Gamma ))\setminus K_q$
is pliant over
$a \in k((\Gamma ))\setminus K_q$
is pliant over
 $K_q$
, then
$K_q$
, then
 $q | [K_q(a) : K_q]$
.
$q | [K_q(a) : K_q]$
.
Proof (1) and (2) follow from the fact that
![]() $k(\Gamma ) \subseteq K_q \subseteq k((\Gamma ))$
. For (3),
$k(\Gamma ) \subseteq K_q \subseteq k((\Gamma ))$
. For (3),
![]() $\operatorname {\mathbb {Z}}$
(resp.
$\operatorname {\mathbb {Z}}$
(resp.
![]() $\mathbb {F}_p[z]$
) is
$\mathbb {F}_p[z]$
) is
![]() $\mathcal {L}_{val}$
-definable in
$\mathcal {L}_{val}$
-definable in
![]() $K_q$
as
$K_q$
as
![]() $K_q \cap (k((\Gamma )))^q$
is
$K_q \cap (k((\Gamma )))^q$
is
![]() $\mathcal {L}_{val}$
-definable in
$\mathcal {L}_{val}$
-definable in
![]() $K_q$
by Lemma 4.7
, and this is sufficient to define
$K_q$
by Lemma 4.7
, and this is sufficient to define
![]() $\operatorname {\mathbb {Z}}$
(resp.
$\operatorname {\mathbb {Z}}$
(resp.
![]() $\mathbb {F}_p[z]$
) by Lemma 4.5
. Finally for (4), note for some n sufficiently large, we have
$\mathbb {F}_p[z]$
) by Lemma 4.5
. Finally for (4), note for some n sufficiently large, we have
![]() $a = a_{n}$
and
$a = a_{n}$
and
![]() $[E_{4n}(a_n) : E_{4n}] = [K_q(a) : K_q]$
, as we assume
$[E_{4n}(a_n) : E_{4n}] = [K_q(a) : K_q]$
, as we assume
![]() $a \not \in K_q$
. By construction (Case 1),
$a \not \in K_q$
. By construction (Case 1),
![]() $q|[E_{4n}(a) : E_{4n}]$
as desired.
$q|[E_{4n}(a) : E_{4n}]$
as desired.
Remark 4.9 [Reference Engler and Prestel13, pp. 173–178]
Let S be an infinite set of indices and
![]() $\mathcal {U}$
a nonprincipal ultrafilter on S. For
$\mathcal {U}$
a nonprincipal ultrafilter on S. For
![]() $s \in S$
, let
$s \in S$
, let
![]() $(K_s, v_s)$
be a valued field. One may take an ultraproduct
$(K_s, v_s)$
be a valued field. One may take an ultraproduct
![]() $\prod _{s \in S} (K_s, v_s)/\mathcal {U}$
of valued fields, and obtain a (valued) field
$\prod _{s \in S} (K_s, v_s)/\mathcal {U}$
of valued fields, and obtain a (valued) field
![]() $\mathbb {K} = \prod _{s \in S} K_s/\mathcal {U}$
with value group
$\mathbb {K} = \prod _{s \in S} K_s/\mathcal {U}$
with value group
![]() $\prod _{s \in S} v_s K_s/\mathcal {U}$
and residue field
$\prod _{s \in S} v_s K_s/\mathcal {U}$
and residue field
![]() $\prod _{s \in S} K_s v_s/\mathcal {U}$
, under the valuation
$\prod _{s \in S} K_s v_s/\mathcal {U}$
, under the valuation
![]() $\prod v_s$
defined by:
$\prod v_s$
defined by:
 $$ \begin{gather*} \textstyle\prod v_s ([(a_s)_{s \in S}]) = [(v_s(a_s))_{s \in S}], \quad \mbox{with residue}\\ res_{\textstyle\prod v_s} : \mathcal{O}_{\textstyle\prod v_s} \rightarrow \prod_{s \in S} K_s v_s/\mathcal{U};\quad [(x_s)] \mapsto [(res_{v_s}(x_s))]. \end{gather*} $$
$$ \begin{gather*} \textstyle\prod v_s ([(a_s)_{s \in S}]) = [(v_s(a_s))_{s \in S}], \quad \mbox{with residue}\\ res_{\textstyle\prod v_s} : \mathcal{O}_{\textstyle\prod v_s} \rightarrow \prod_{s \in S} K_s v_s/\mathcal{U};\quad [(x_s)] \mapsto [(res_{v_s}(x_s))]. \end{gather*} $$
(Here
![]() $a_s \in K_s$
for
$a_s \in K_s$
for
![]() $s \in S$
, and
$s \in S$
, and
![]() $[\cdot ]$
represents the equivalence class of tuples modulo
$[\cdot ]$
represents the equivalence class of tuples modulo
![]() $\mathcal {U}$
.)
$\mathcal {U}$
.)
Corollary 4.10. Let
![]() $(K, v)$
be an equicharacteristic
$(K, v)$
be an equicharacteristic
![]() $0$
henselian nontrivially valued field.
$0$
henselian nontrivially valued field.
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
![]() $\mathcal {O}_v$
is
$\mathcal {O}_v$
is
![]() $\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
$\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
Proof Writing
![]() $k = Kv$
and
$k = Kv$
and
![]() $\Gamma = vK$
, by Theorem 4.6
we have
$\Gamma = vK$
, by Theorem 4.6
we have
![]() $(K, v) \equiv (k((\Gamma )), v_{\Gamma })$
. By the Downwards Löwenheim–Skolem Theorem we may also assume
$(K, v) \equiv (k((\Gamma )), v_{\Gamma })$
. By the Downwards Löwenheim–Skolem Theorem we may also assume
![]() $k, \Gamma $
are countable. Set
$k, \Gamma $
are countable. Set
![]() $v'$
(on k) to be the trivial valuation, in which case
$v'$
(on k) to be the trivial valuation, in which case
![]() $v = v' \circ v_{\Gamma } = v_{\Gamma }$
. By Lemma 4.1
,
$v = v' \circ v_{\Gamma } = v_{\Gamma }$
. By Lemma 4.1
,
![]() $(R, v_R)\! =\! (k(\Gamma ), v_{\Gamma }|_{k(\Gamma )}),(Z, v_Z)\! = \!(k((\Gamma )), v_{\Gamma }), F\! =\! k((\Gamma )) \cap \widetilde {k(\Gamma )}$
satisfy Assumption
$(R, v_R)\! =\! (k(\Gamma ), v_{\Gamma }|_{k(\Gamma )}),(Z, v_Z)\! = \!(k((\Gamma )), v_{\Gamma }), F\! =\! k((\Gamma )) \cap \widetilde {k(\Gamma )}$
satisfy Assumption
![]() $(\otimes )$
.
$(\otimes )$
.
Let q be prime and consider
![]() $(K_q, w = v_{\Gamma }|_{K_q}) \subseteq (k((\Gamma )), v_{\Gamma })$
arising from the Modified Construction, where now “pliant” means algebraic. In particular
$(K_q, w = v_{\Gamma }|_{K_q}) \subseteq (k((\Gamma )), v_{\Gamma })$
arising from the Modified Construction, where now “pliant” means algebraic. In particular
![]() $K_q$
is an equicharacteristic
$K_q$
is an equicharacteristic
![]() $0$
valued field with residue field k and value group
$0$
valued field with residue field k and value group
![]() $\Gamma $
. We will verify the henselianity axioms
$\Gamma $
. We will verify the henselianity axioms
![]() $\varphi _1, \dots , \varphi _{q-1}$
are satisfied, where
$\varphi _1, \dots , \varphi _{q-1}$
are satisfied, where
![]() $\varphi _n$
is
$\varphi _n$
is
 $$\begin{align*}\forall a_0, \dots, a_{n-2} \left( \bigwedge_i a_i \in \mathfrak{m}_v \rightarrow \exists x\, [x^n + x^{n-1} + a_{n-2} x^{n-2} + \dots + a_0 = 0]\right).\end{align*}$$
$$\begin{align*}\forall a_0, \dots, a_{n-2} \left( \bigwedge_i a_i \in \mathfrak{m}_v \rightarrow \exists x\, [x^n + x^{n-1} + a_{n-2} x^{n-2} + \dots + a_0 = 0]\right).\end{align*}$$
Take
![]() $l \leq q-1$
and fix
$l \leq q-1$
and fix
![]() $a_0, \dots , a_{l-2} \in \mathfrak {m}_{w}$
. Suppose
$a_0, \dots , a_{l-2} \in \mathfrak {m}_{w}$
. Suppose
![]() $X^l + X^{l-1} + a_{l-2} X^{l-2} + \dots + a_0 = 0$
has no solution in
$X^l + X^{l-1} + a_{l-2} X^{l-2} + \dots + a_0 = 0$
has no solution in
![]() $K_q$
, and
$K_q$
, and
![]() $\alpha \in k((\Gamma )) \setminus K_q$
satisfies this equation. Then
$\alpha \in k((\Gamma )) \setminus K_q$
satisfies this equation. Then
![]() $K_q(\alpha )/K_q$
is a finite proper extension. By Theorem 4.8
,
$K_q(\alpha )/K_q$
is a finite proper extension. By Theorem 4.8
,
![]() $q| [K_q(\alpha ) : K_q]$
, however
$q| [K_q(\alpha ) : K_q]$
, however
![]() $q> l$
and
$q> l$
and
![]() $[K_q(\alpha ) : K_q] \leq l$
; a contradiction. We conclude that
$[K_q(\alpha ) : K_q] \leq l$
; a contradiction. We conclude that
![]() $K_q \models \varphi _l$
for all
$K_q \models \varphi _l$
for all
![]() $l \leq q-1$
; in particular for
$l \leq q-1$
; in particular for
![]() $n \geq 0$
fixed,
$n \geq 0$
fixed,
![]() $K_q \models \varphi _n$
for all primes
$K_q \models \varphi _n$
for all primes
![]() $q> n$
.
$q> n$
.
Let
![]() $\mathcal {U}$
be a nonprincipal ultrafilter on the set of primes, and let
$\mathcal {U}$
be a nonprincipal ultrafilter on the set of primes, and let
![]() $\mathbb {K}$
be the ultraproduct
$\mathbb {K}$
be the ultraproduct
![]() $\prod _{q} K_q / \mathcal {U}$
. By Remark 4.9 and Łoś’ Theorem,
$\prod _{q} K_q / \mathcal {U}$
. By Remark 4.9 and Łoś’ Theorem,
![]() $\mathbb {K}$
is an equicharacteristic
$\mathbb {K}$
is an equicharacteristic
![]() $0$
henselian valued field with residue field (
$0$
henselian valued field with residue field (
![]() $\mathcal {L}_r$
-elementarily equivalent to) k, and value group (
$\mathcal {L}_r$
-elementarily equivalent to) k, and value group (
![]() $\mathcal {L}_{oag}$
-elementarily equivalent to)
$\mathcal {L}_{oag}$
-elementarily equivalent to)
![]() $\Gamma $
. Hence by Theorem 4.6
,
$\Gamma $
. Hence by Theorem 4.6
,
![]() $\mathbb {K} \equiv _{\mathcal {L}_{val}} k((\Gamma ))$
. Thus
$\mathbb {K} \equiv _{\mathcal {L}_{val}} k((\Gamma ))$
. Thus
![]() $\mathbb {K} \models T$
for any finite subtheory
$\mathbb {K} \models T$
for any finite subtheory
![]() $T \subseteq {\mathtt{Th}}(k((\Gamma )); \mathcal {L}_{val})$
, and hence for some prime q,
$T \subseteq {\mathtt{Th}}(k((\Gamma )); \mathcal {L}_{val})$
, and hence for some prime q,
![]() $K_q \models T$
. By Theorem 4.8 and Corollary 1.8
,
$K_q \models T$
. By Theorem 4.8 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable, making T undecidable as required.
${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable, making T undecidable as required.
Finally, if
![]() $\mathcal {O}_v \subseteq K$
is
$\mathcal {O}_v \subseteq K$
is
![]() $\mathcal {L}_r$
-definable by the formula
$\mathcal {L}_r$
-definable by the formula
![]() $\varpi (x, \overline {y})$
(where
$\varpi (x, \overline {y})$
(where
![]() $\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
$\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
![]() $\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
$\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
![]() $S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
$S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
![]() $K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
$K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
5. Henselian valued fields: further discourse
We may extend the results of the previous section from equicharacteristic 0 henselian valued fields, to mixed characteristic henselian valued fields, using the standard decomposition Footnote 5 :
Let
![]() $(K, v)$
be a valued field of mixed characteristic
$(K, v)$
be a valued field of mixed characteristic
![]() $(0, p)$
with value group
$(0, p)$
with value group
![]() $\Gamma $
. Define
$\Gamma $
. Define
![]() $\Delta _0$
to be the minimal convex subgroup of
$\Delta _0$
to be the minimal convex subgroup of
![]() $\Gamma $
containing
$\Gamma $
containing
![]() $v(p)$
, and
$v(p)$
, and
![]() $\Delta _p$
to be the maximal convex subgroup of
$\Delta _p$
to be the maximal convex subgroup of
![]() $\Gamma $
not containing
$\Gamma $
not containing
![]() $v(p)$
. We will consider the valuation(s)
$v(p)$
. We will consider the valuation(s)
![]() $v_0 : K \rightarrow \Gamma / \Delta _0$
(resp.
$v_0 : K \rightarrow \Gamma / \Delta _0$
(resp.
![]() $v_p : K \rightarrow \Gamma / \Delta _p$
) corresponding to the coarsening(s) of v with respect to
$v_p : K \rightarrow \Gamma / \Delta _p$
) corresponding to the coarsening(s) of v with respect to
![]() $\Delta _0$
(resp.
$\Delta _0$
(resp.
![]() $\Delta _p$
), and the induced valuation(s)
$\Delta _p$
), and the induced valuation(s)
![]() $\hat {v}_0 : K v_0 \rightarrow \Delta _0$
(resp.
$\hat {v}_0 : K v_0 \rightarrow \Delta _0$
(resp.
![]() $\hat {v}_p : K v_p \rightarrow \Delta _p$
) with residue field(s)
$\hat {v}_p : K v_p \rightarrow \Delta _p$
) with residue field(s)
![]() $Kv$
. Also consider
$Kv$
. Also consider
![]() $\overline {v_p} : K v_0 \rightarrow \Delta _0 / \Delta _p$
with residue field
$\overline {v_p} : K v_0 \rightarrow \Delta _0 / \Delta _p$
with residue field
![]() $K v_p$
; this arises as the coarsening of
$K v_p$
; this arises as the coarsening of
![]() $v_0$
with respect to
$v_0$
with respect to
![]() $\Delta _p$
(as
$\Delta _p$
(as
![]() $\Delta _p < \Delta _0 \leq \Gamma $
). These fit together in the following way:
$\Delta _p < \Delta _0 \leq \Gamma $
). These fit together in the following way:


If
![]() $\Delta _0 = vK$
then by the Compactness Theorem there is an elementary extension
$\Delta _0 = vK$
then by the Compactness Theorem there is an elementary extension
![]() $(K, v) \prec (K^{\flat }, v^{\flat })$
containing an element
$(K, v) \prec (K^{\flat }, v^{\flat })$
containing an element
![]() $c^{\flat }$
such that
$c^{\flat }$
such that
![]() $n \cdot v^{\flat }(p) < v^{\flat }(c^{\flat }) < \infty $
for all
$n \cdot v^{\flat }(p) < v^{\flat }(c^{\flat }) < \infty $
for all
![]() $n \geq 0$
. Hence the minimal convex subgroup of
$n \geq 0$
. Hence the minimal convex subgroup of
![]() $v^{\flat }K^{\flat }$
containing
$v^{\flat }K^{\flat }$
containing
![]() $v^{\flat }(p)$
does not contain
$v^{\flat }(p)$
does not contain
![]() $v^{\flat }(c^{\flat })$
, i.e.,
$v^{\flat }(c^{\flat })$
, i.e.,
![]() $\Delta _0 < v^{\flat }K^{\flat }$
. As
$\Delta _0 < v^{\flat }K^{\flat }$
. As
![]() $(K, v) \equiv (K^{\flat }, v^{\flat })$
, for the purposes of proving finite undecidability we may assume WLOG
$(K, v) \equiv (K^{\flat }, v^{\flat })$
, for the purposes of proving finite undecidability we may assume WLOG
![]() $\Delta _0 < vK$
. Consider:
$\Delta _0 < vK$
. Consider:
Lemma 5.1 [Reference Anscombe and Jahnke2, Lemma 6.5]
Let T be a theory of bivalued fields
![]() $(K, v', v)$
with
$(K, v', v)$
with
![]() $v'$
an equicharacteristic
$v'$
an equicharacteristic
![]() $0$
henselian coarsening of v, and suppose that T entails complete theories of valued fields
$0$
henselian coarsening of v, and suppose that T entails complete theories of valued fields
![]() $(K, v')$
and
$(K, v')$
and
![]() $(Kv', \overline {v})$
. Then T is complete.
$(Kv', \overline {v})$
. Then T is complete.
Corollary 5.2. Let
![]() $(K, v)$
be a mixed characteristic henselian nontrivially valued field, and
$(K, v)$
be a mixed characteristic henselian nontrivially valued field, and
![]() $v_0$
as above. There exists a nontrivial ordered abelian group
$v_0$
as above. There exists a nontrivial ordered abelian group
![]() $\Omega $
such that
$\Omega $
such that
![]() $(K, v_0, v) \equiv (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
.
$(K, v_0, v) \equiv (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
.
Proof Define
![]() $\Omega = vK/\Delta _0$
. By Theorem 4.6
,
$\Omega = vK/\Delta _0$
. By Theorem 4.6
,
![]() $(K, v_0) \equiv (Kv_0((\Omega )), v_{\Omega })$
. Since
$(K, v_0) \equiv (Kv_0((\Omega )), v_{\Omega })$
. Since
![]() $v = \widehat {v}_0 \circ v_0$
in the standard decomposition of
$v = \widehat {v}_0 \circ v_0$
in the standard decomposition of
![]() $(K, v)$
,
$(K, v)$
,
 $$ \begin{align*} &(Kv_0, \widehat{v}_0) \qquad \mbox{(residue field of}\ (K, v_0)\ \mbox{with the induced valuation)}\\ =\,\, &(Kv_0, \widehat{v}_0) \qquad \mbox{(residue field of}\ (Kv_0((\Omega)), v_{\Omega})\ \mbox{with the induced valuation).} \end{align*} $$
$$ \begin{align*} &(Kv_0, \widehat{v}_0) \qquad \mbox{(residue field of}\ (K, v_0)\ \mbox{with the induced valuation)}\\ =\,\, &(Kv_0, \widehat{v}_0) \qquad \mbox{(residue field of}\ (Kv_0((\Omega)), v_{\Omega})\ \mbox{with the induced valuation).} \end{align*} $$
By Lemma 5.1
, we conclude
![]() $(K, v_0, v) \equiv (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
as desired.
$(K, v_0, v) \equiv (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
as desired.
Theorem 5.3. Let
![]() $(K, v)$
be a mixed characteristic henselian nontrivially valued field.
$(K, v)$
be a mixed characteristic henselian nontrivially valued field.
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
![]() $\mathcal {O}_v$
is
$\mathcal {O}_v$
is
![]() $\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
$\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
Proof As finite undecidability is a property of
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
, we may assume WLOG
${\mathtt{Th}}(K; \mathcal {L}_{val})$
, we may assume WLOG
![]() $(K, v_0, v) = (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
where
$(K, v_0, v) = (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
where
![]() $Kv_0$
and
$Kv_0$
and
![]() $\Omega $
are countable, by the Downwards Löwenheim–Skolem Theorem and Corollary 5.2
. Let
$\Omega $
are countable, by the Downwards Löwenheim–Skolem Theorem and Corollary 5.2
. Let
![]() $(Z, v_Z) = (Kv_0((\Omega )), \widehat {v}_0 \circ v_{\Omega })$
,
$(Z, v_Z) = (Kv_0((\Omega )), \widehat {v}_0 \circ v_{\Omega })$
,
![]() $(R, v_R) = (Kv_0(\Omega ),\, \widehat {v}_0 \circ v_{\Omega })$
and
$(R, v_R) = (Kv_0(\Omega ),\, \widehat {v}_0 \circ v_{\Omega })$
and
![]() $F = Z \cap \widetilde {R}$
. By Lemma 4.1
, Assumption
$F = Z \cap \widetilde {R}$
. By Lemma 4.1
, Assumption
![]() $(\otimes )$
is satisfied: for
$(\otimes )$
is satisfied: for
![]() $q> p$
prime, denote by
$q> p$
prime, denote by
![]() $K_q$
be the field given by the Modified Construction—where now “pliant” means algebraic—with valuation
$K_q$
be the field given by the Modified Construction—where now “pliant” means algebraic—with valuation
![]() $(\widehat {v}_0 \circ v_{\Omega })|_{K_q} = \widehat {v}_0 \circ v_{\Omega }|_{K_q}$
. We have the following diagram of fields:
$(\widehat {v}_0 \circ v_{\Omega })|_{K_q} = \widehat {v}_0 \circ v_{\Omega }|_{K_q}$
. We have the following diagram of fields:

Consider
![]() $K_q$
as a multisorted structure:
$K_q$
as a multisorted structure:
which encompasses the diagram

Let
![]() $\mathcal {U}$
be a nonprincipal ultrafilter on the set of primes larger than p, and let
$\mathcal {U}$
be a nonprincipal ultrafilter on the set of primes larger than p, and let
![]() $\mathbb {K}$
be the ultraproduct
$\mathbb {K}$
be the ultraproduct
![]() $\prod _{q>p} \mathcal {K}_q/\mathcal {U}$
. (We abuse notation to also denote the home sort of
$\prod _{q>p} \mathcal {K}_q/\mathcal {U}$
. (We abuse notation to also denote the home sort of
![]() $\mathbb {K}$
by
$\mathbb {K}$
by
![]() $\mathbb {K}$
.) We have the following properties of
$\mathbb {K}$
.) We have the following properties of
![]() $\mathbb {K}$
:
$\mathbb {K}$
:
-
•
 $\mathbb {K}$
has valuation
$\mathbb {K}$
has valuation
 $\mathfrak {v}_0=\prod v_{\Omega }|_{K_q}$
with residue field
$\mathfrak {v}_0=\prod v_{\Omega }|_{K_q}$
with residue field
 $\prod _{q>p} Kv_0/\mathcal {U} = Kv_0^{\mathcal {U}}$
and value group
$\prod _{q>p} Kv_0/\mathcal {U} = Kv_0^{\mathcal {U}}$
and value group
 $\prod _{q>p} \Omega /\mathcal {U} = \Omega ^{\mathcal {U}}$
. (This is Remark 4.9
.) Furthermore,
$\prod _{q>p} \Omega /\mathcal {U} = \Omega ^{\mathcal {U}}$
. (This is Remark 4.9
.) Furthermore,
 $(\mathbb {K}, \mathfrak {v}_0)$
is a henselian valued field. Indeed, we claim for
$(\mathbb {K}, \mathfrak {v}_0)$
is a henselian valued field. Indeed, we claim for
 $q> p$
prime the henselianity axioms
$q> p$
prime the henselianity axioms
 $\varphi _1, \dots , \varphi _{q-1}$
are satisfied in
$\varphi _1, \dots , \varphi _{q-1}$
are satisfied in
 $K_q$
:
$K_q$
:Let
 $l < q$
and fix
$l < q$
and fix
 $a_0, \dots a_{l-2} \in \mathfrak {m}_{v_{\Omega }|_{K_q}}$
. Suppose
$a_0, \dots a_{l-2} \in \mathfrak {m}_{v_{\Omega }|_{K_q}}$
. Suppose
 $X^l + X^{l-1} + a_{l-2}X^{l-2} + \dots + a_0 = 0$
has no solution in
$X^l + X^{l-1} + a_{l-2}X^{l-2} + \dots + a_0 = 0$
has no solution in
 $K_q$
—though there exists a solution
$K_q$
—though there exists a solution
 $\alpha \in K_q^h$
, and
$\alpha \in K_q^h$
, and
 $K_q^h \subseteq Kv_0((\Omega ))$
by the universal property of henselisations [Reference Engler and Prestel13, Theorem 5.2.2]. Then
$K_q^h \subseteq Kv_0((\Omega ))$
by the universal property of henselisations [Reference Engler and Prestel13, Theorem 5.2.2]. Then
 $K_q(\alpha )/K_q$
is a finite proper extension. By Theorem 4.8
,
$K_q(\alpha )/K_q$
is a finite proper extension. By Theorem 4.8
,
 $q|[K_q(\alpha ) : K_q]$
; however
$q|[K_q(\alpha ) : K_q]$
; however
 $q> l$
and
$q> l$
and
 $[K_q(\alpha ) : K_q] \leq l$
; a contradiction.
$[K_q(\alpha ) : K_q] \leq l$
; a contradiction.Therefore, by Łoś’ Theorem (i.e., [Reference Chang and Keisler6, Theorem 4.1.9])
 $(\mathbb {K}, \mathfrak {v}_0)$
is an equicharacteristic 0 henselian valued field with
$(\mathbb {K}, \mathfrak {v}_0)$
is an equicharacteristic 0 henselian valued field with
 $\mathfrak {v}_0 \mathbb {K} \equiv _{\mathcal {L}_{oag}} \Omega $
and
$\mathfrak {v}_0 \mathbb {K} \equiv _{\mathcal {L}_{oag}} \Omega $
and
 $\mathbb {K}\mathfrak {v}_0 \equiv _{\mathcal {L}_r} Kv_0$
. By Theorem 4.6
we conclude
$\mathbb {K}\mathfrak {v}_0 \equiv _{\mathcal {L}_r} Kv_0$
. By Theorem 4.6
we conclude
 $(\mathbb {K}, \mathfrak {v}_0) \equiv (Kv_0((\Omega )), v_{\Omega })$
.
$(\mathbb {K}, \mathfrak {v}_0) \equiv (Kv_0((\Omega )), v_{\Omega })$
. -
•
 $Kv_0^{\mathcal {U}}$
has valuation
$Kv_0^{\mathcal {U}}$
has valuation
 $\widehat {v}_0^{\mathcal {U}} = \prod \widehat {v}_0$
with residue field
$\widehat {v}_0^{\mathcal {U}} = \prod \widehat {v}_0$
with residue field
 $vK^{\mathcal {U}}$
and value group
$vK^{\mathcal {U}}$
and value group
 $\Delta _0^{\mathcal {U}}$
(Remark 4.9
). By [Reference Chang and Keisler6, Theorem 4.1.9],
$\Delta _0^{\mathcal {U}}$
(Remark 4.9
). By [Reference Chang and Keisler6, Theorem 4.1.9],
 $(Kv_0^{\mathcal {U}}, \widehat {v}_0^{\mathcal {U}}) \equiv (Kv_0, \widehat {v}_0)$
.
$(Kv_0^{\mathcal {U}}, \widehat {v}_0^{\mathcal {U}}) \equiv (Kv_0, \widehat {v}_0)$
. -
• Hence
 $\mathbb {K}$
can be equipped with a valuation
$\mathbb {K}$
can be equipped with a valuation
 $\mathfrak {v}_1 := \widehat {v}_0^{\mathcal {U}} \circ \mathfrak {v}_0$
, and
$\mathfrak {v}_1 := \widehat {v}_0^{\mathcal {U}} \circ \mathfrak {v}_0$
, and
 $\mathfrak {v}_0$
is an equicharacteristic
$\mathfrak {v}_0$
is an equicharacteristic
 $0$
henselian coarsening of
$0$
henselian coarsening of
 $\mathfrak {v}_1$
.
$\mathfrak {v}_1$
.
 $\mathbb {K}$
also has a valuation
$\mathbb {K}$
also has a valuation
 $\mathfrak {v}_2=\prod (\widehat {v}_0 \circ v_{\Omega })|_{K_q}$
, and we claim
$\mathfrak {v}_2=\prod (\widehat {v}_0 \circ v_{\Omega })|_{K_q}$
, and we claim
 $\mathcal {O}_{\mathfrak {v}_1} = \mathcal {O}_{\mathfrak {v}_2}$
, so
$\mathcal {O}_{\mathfrak {v}_1} = \mathcal {O}_{\mathfrak {v}_2}$
, so
 $(\mathbb {K}, \mathfrak {v}_1) \equiv (\mathbb {K}, \mathfrak {v}_2)$
. Indeed,
$(\mathbb {K}, \mathfrak {v}_1) \equiv (\mathbb {K}, \mathfrak {v}_2)$
. Indeed,  $$ \begin{align*} x = [(x_q)] \in \mathcal{O}_{\mathfrak{v}_1} &\iff [(x_q)] \in res_{\mathfrak{v}_0}^{-1}(\mathcal{O}_{\widehat{v}_0^{\mathcal{U}}})\\ &\iff res_{\mathfrak{v}_0}([(x_q)]) = [(res_{v_{\Omega}|_{K_q}}(x_q))] \in \mathcal{O}_{\widehat{v}_0^{\mathcal{U}}}\\ &\iff \{q \mbox{ : } res_{v_{\Omega}|_{K_q}}(x_q) \in \mathcal{O}_{\widehat{v}_0}\} \in \mathcal{U}\\ &\iff \{q \mbox{ : } x_q \in \mathcal{O}_{(\widehat{v}_0 \circ v_{\Omega})|_{K_q}}\} \in \mathcal{U} \iff [(x_q)] \in \mathcal{O}_{\mathfrak{v}_2}. \end{align*} $$
$$ \begin{align*} x = [(x_q)] \in \mathcal{O}_{\mathfrak{v}_1} &\iff [(x_q)] \in res_{\mathfrak{v}_0}^{-1}(\mathcal{O}_{\widehat{v}_0^{\mathcal{U}}})\\ &\iff res_{\mathfrak{v}_0}([(x_q)]) = [(res_{v_{\Omega}|_{K_q}}(x_q))] \in \mathcal{O}_{\widehat{v}_0^{\mathcal{U}}}\\ &\iff \{q \mbox{ : } res_{v_{\Omega}|_{K_q}}(x_q) \in \mathcal{O}_{\widehat{v}_0}\} \in \mathcal{U}\\ &\iff \{q \mbox{ : } x_q \in \mathcal{O}_{(\widehat{v}_0 \circ v_{\Omega})|_{K_q}}\} \in \mathcal{U} \iff [(x_q)] \in \mathcal{O}_{\mathfrak{v}_2}. \end{align*} $$
Considering
![]() $(\mathbb {K}, \mathfrak {v}_0, \mathfrak {v}_1)$
as a bivalued field, by Lemma 5.1
$(\mathbb {K}, \mathfrak {v}_0, \mathfrak {v}_1)$
as a bivalued field, by Lemma 5.1
Taking a reduct of the language,
![]() $(\mathbb {K}, \mathfrak {v}_2) \equiv (\mathbb {K}, \mathfrak {v}_1) \equiv (K, v)$
. Therefore if T is a finite subtheory of
$(\mathbb {K}, \mathfrak {v}_2) \equiv (\mathbb {K}, \mathfrak {v}_1) \equiv (K, v)$
. Therefore if T is a finite subtheory of
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
,
${\mathtt{Th}}(K; \mathcal {L}_{val})$
,
![]() $(\mathbb {K}, \mathfrak {v}_2) \models T$
, and hence for some q sufficiently large,
$(\mathbb {K}, \mathfrak {v}_2) \models T$
, and hence for some q sufficiently large,
![]() $(K_q, \widehat {v}_0 \circ v_{\Omega }|_{K_q}) \models T$
. By Theorem 4.8 and Corollary 1.8
,
$(K_q, \widehat {v}_0 \circ v_{\Omega }|_{K_q}) \models T$
. By Theorem 4.8 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable, making T undecidable as required.
${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable, making T undecidable as required.
Finally, if
![]() $\mathcal {O}_v \subseteq K$
is
$\mathcal {O}_v \subseteq K$
is
![]() $\mathcal {L}_r$
-definable by the formula
$\mathcal {L}_r$
-definable by the formula
![]() $\varpi (x, \overline {y})$
(where
$\varpi (x, \overline {y})$
(where
![]() $\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
$\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
![]() $\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O}_{\mathfrak {v}_2} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
$\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O}_{\mathfrak {v}_2} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
![]() $S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
$S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
![]() $K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
$K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
What remains is to handle the case of equicharacteristic
![]() $p> 0$
henselian nontrivially valued fields. We will show this gap can be eliminated for certain fields of this type (e.g., those fields also satisfying NIP, by using a nice algebraic classification of such fields by Anscombe and Jahnke [Reference Anscombe and Jahnke2, Theorem 5.1]). We require the following definitions:
$p> 0$
henselian nontrivially valued fields. We will show this gap can be eliminated for certain fields of this type (e.g., those fields also satisfying NIP, by using a nice algebraic classification of such fields by Anscombe and Jahnke [Reference Anscombe and Jahnke2, Theorem 5.1]). We require the following definitions:
Definition 5.4. A valued field
![]() $(K, v)$
is said to be (separably) defectless if whenever
$(K, v)$
is said to be (separably) defectless if whenever
![]() $L/K$
is a finite (separable) extension,
$L/K$
is a finite (separable) extension,
![]() $[L : K] = \sum _{w \supseteq v} e(w/v) f(w/v)$
, where w ranges over all prolongations of v to L,
$[L : K] = \sum _{w \supseteq v} e(w/v) f(w/v)$
, where w ranges over all prolongations of v to L,
![]() $e(w/v) = (wL : vK)$
is the ramification degree and
$e(w/v) = (wL : vK)$
is the ramification degree and
![]() $f(w/v) = [Lw : Kv]$
is the inertia degree of the valued field extension
$f(w/v) = [Lw : Kv]$
is the inertia degree of the valued field extension
![]() $(L,w)/(K,v)$
.
$(L,w)/(K,v)$
.
Definition 5.5. A valued field
![]() $(K, v)$
of residue characteristic
$(K, v)$
of residue characteristic
![]() $p>0$
is Kaplansky
Footnote
6
if
$p>0$
is Kaplansky
Footnote
6
if
![]() $vK$
is p-divisible, and
$vK$
is p-divisible, and
![]() $Kv$
is perfect and admits no proper separable algebraic extensions of degree divisible by p.
$Kv$
is perfect and admits no proper separable algebraic extensions of degree divisible by p.
Theorem 5.6 (Anscombe–Jahnke)
Let
![]() $(K, v)$
be a positive equicharacteristic NIP henselian nontrivially valued field. Then
$(K, v)$
be a positive equicharacteristic NIP henselian nontrivially valued field. Then
![]() $(K, v)$
is separably defectless Kaplansky.
$(K, v)$
is separably defectless Kaplansky.
Proof An immediate consequence of [Reference Anscombe and Jahnke2, Proposition 3.1].
A corollary to this, noted by Anscombe and Jahnke, is that by Delon [Reference Delon10, Théorème 3.1] the
![]() $\mathcal {L}_{val}$
-theory of equicharacteristic
$\mathcal {L}_{val}$
-theory of equicharacteristic
![]() $p> 0$
henselian separably defectless valued fields
$p> 0$
henselian separably defectless valued fields
![]() $(K,v)$
of imperfection degree e, with residue field
$(K,v)$
of imperfection degree e, with residue field
![]() $\mathcal {L}_r$
-elementarily equivalent to
$\mathcal {L}_r$
-elementarily equivalent to
![]() $Kv$
and value group
$Kv$
and value group
![]() $\mathcal {L}_{oag}$
-elementarily equivalent to
$\mathcal {L}_{oag}$
-elementarily equivalent to
![]() $vK$
, is complete. (As we are concerned with finitely axiomatised subsets of
$vK$
, is complete. (As we are concerned with finitely axiomatised subsets of
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
, we will assume WLOG
${\mathtt{Th}}(K; \mathcal {L}_{val})$
, we will assume WLOG
![]() $e < \infty $
.)
$e < \infty $
.)
For a valued field
![]() $(B, v_B)$
to be separably defectless, it is sufficient for it to satisfy the first-order
$(B, v_B)$
to be separably defectless, it is sufficient for it to satisfy the first-order
![]() $\mathcal {L}_{val}$
-statementsFootnote
7
$\mathcal {L}_{val}$
-statementsFootnote
7
![]() for all
for all
![]() $M \geq 1$
:
$M \geq 1$
:
 $$\begin{align} & \mbox{For all finite separable extensions}\ D/B\ \text{of degree}\ \leq M,\ \text{the equality} \nonumber\\ &\hspace{37mm}[D : B] = \sum_{w \supseteq v_B} e(w/v_B) f(w/v_B)\hspace{7mm} \\ &\mbox{holds, where}\ w\ \text{ranges over all prolongations of}\ v_B\ \text{to}\ D,\ e(w/v_B)\ \text{is} \nonumber\\ &\mbox{the ramification index and}\ f(w/v_B)\ \text{is the inertia degree.} \nonumber \end{align}$$
$$\begin{align} & \mbox{For all finite separable extensions}\ D/B\ \text{of degree}\ \leq M,\ \text{the equality} \nonumber\\ &\hspace{37mm}[D : B] = \sum_{w \supseteq v_B} e(w/v_B) f(w/v_B)\hspace{7mm} \\ &\mbox{holds, where}\ w\ \text{ranges over all prolongations of}\ v_B\ \text{to}\ D,\ e(w/v_B)\ \text{is} \nonumber\\ &\mbox{the ramification index and}\ f(w/v_B)\ \text{is the inertia degree.} \nonumber \end{align}$$
Lemma 5.7. Fix
![]() $M \in \operatorname {\mathbb {N}}_{>0}$
and
$M \in \operatorname {\mathbb {N}}_{>0}$
and
![]() $q> M^M$
prime. Assume
$q> M^M$
prime. Assume
![]() $(R, v_R)$
,
$(R, v_R)$
,
![]() $(Z, v_Z)$
, and F satisfy Assumption
$(Z, v_Z)$
, and F satisfy Assumption
![]() $(\otimes )$
and let
$(\otimes )$
and let
![]() $K_q$
be the field resulting from the Modified Construction. If Z is separably defectless Kaplansky, then
$K_q$
be the field resulting from the Modified Construction. If Z is separably defectless Kaplansky, then ![]() .
.
Proof Let
![]() $D/K_q$
be a separable extension of degree
$D/K_q$
be a separable extension of degree
![]() $\leq M$
. By taking the normal closure may assume
$\leq M$
. By taking the normal closure may assume
![]() $D/K_q$
is Galois and of degree
$D/K_q$
is Galois and of degree
![]() $d\leq M^M$
. If
$d\leq M^M$
. If
![]() $D/K_q$
is proper, by degree reasons
$D/K_q$
is proper, by degree reasons
![]() $Z \cap D = K_q$
. Indeed, if
$Z \cap D = K_q$
. Indeed, if
![]() $Z \supset D' \supset K_q$
is a separable extension of degree
$Z \supset D' \supset K_q$
is a separable extension of degree
![]() $\leq M^M$
, by the Primitive Element Theorem there exists
$\leq M^M$
, by the Primitive Element Theorem there exists
![]() $\alpha \in Z \cap K_q^s$
such that
$\alpha \in Z \cap K_q^s$
such that
![]() $D' = K_q(\alpha )$
. By Theorem 4.8
, if
$D' = K_q(\alpha )$
. By Theorem 4.8
, if
![]() $\alpha \not \in K_q$
then
$\alpha \not \in K_q$
then
![]() $q | [K_q(\alpha ) : K_q]$
; however
$q | [K_q(\alpha ) : K_q]$
; however
![]() $q> M^M$
and
$q> M^M$
and
![]() $[K_q(\alpha ) : K_q] \leq M^M$
. This is a contradiction; hence
$[K_q(\alpha ) : K_q] \leq M^M$
. This is a contradiction; hence
![]() $\alpha \in K_q$
. Thus Z and D are linearly disjoint over
$\alpha \in K_q$
. Thus Z and D are linearly disjoint over
![]() $K_q$
. Consider the following tower of extensions:
$K_q$
. Consider the following tower of extensions:

By the tower property [Reference Fried and Jarden16, Lemma 2.5.3], D is linearly disjoint to
![]() $K_q^h$
, a subfield of Z by the universal property of henselisations. Thus
$K_q^h$
, a subfield of Z by the universal property of henselisations. Thus
![]() $w = v_Z|_{K_q}$
extends uniquely to
$w = v_Z|_{K_q}$
extends uniquely to
![]() $(D, w')$
, by, e.g., [Reference Blaszczok and Kuhlmann4, Lemma 2.1]. As
$(D, w')$
, by, e.g., [Reference Blaszczok and Kuhlmann4, Lemma 2.1]. As
![]() $(Z, v_Z)$
is henselian,
$(Z, v_Z)$
is henselian,
![]() $v_Z$
extends uniquely to
$v_Z$
extends uniquely to
![]() $(ZD, v_Z')$
, and restricts to
$(ZD, v_Z')$
, and restricts to
![]() $(D, w')$
. As
$(D, w')$
. As
![]() $Z/K_q$
is immediate, as the valuation extensions are unique, and as Z is linearly disjoint from D over
$Z/K_q$
is immediate, as the valuation extensions are unique, and as Z is linearly disjoint from D over
![]() $K_q$
,
$K_q$
,
 $$ \begin{align*} p^{\nu} e(w'/w) f(w'/w) &= [D : K_q] \qquad\mbox{where}\ \nu \geq 0,\ \mbox{by [13, Theorem 3.3.3],}\\ &= [ZD : Z] \qquad \mbox{by [16, Corollary 2.5.2],}\\ &= e(v_Z'/v_Z) f(v_Z' / v_Z) \qquad\mbox{as}\ Z\ \mbox{is separably defectless}. \end{align*} $$
$$ \begin{align*} p^{\nu} e(w'/w) f(w'/w) &= [D : K_q] \qquad\mbox{where}\ \nu \geq 0,\ \mbox{by [13, Theorem 3.3.3],}\\ &= [ZD : Z] \qquad \mbox{by [16, Corollary 2.5.2],}\\ &= e(v_Z'/v_Z) f(v_Z' / v_Z) \qquad\mbox{as}\ Z\ \mbox{is separably defectless}. \end{align*} $$
In addition, as Z is Kaplansky,
![]() $p \nmid e(v_Z'/v_Z), f(v_Z' / v_Z)$
. Hence
$p \nmid e(v_Z'/v_Z), f(v_Z' / v_Z)$
. Hence
We conclude ![]() as desired.
as desired.
We are ready to prove:
Theorem 5.8. Let
![]() $(K, v)$
be an equicharacteristic
$(K, v)$
be an equicharacteristic
![]() $p> 0$
separably defectless Kaplansky henselian nontrivially valued field.
$p> 0$
separably defectless Kaplansky henselian nontrivially valued field.
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
![]() $\mathcal {O}_v$
is
$\mathcal {O}_v$
is
![]() $\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
$\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
Proof Fix
![]() $e \in \operatorname {\mathbb {N}}$
, the imperfection degree of K. Let k,
$e \in \operatorname {\mathbb {N}}$
, the imperfection degree of K. Let k,
![]() $\Gamma $
be countable models of
$\Gamma $
be countable models of
![]() ${\mathtt{Th}}(Kv; \mathcal {L}_r)$
,
${\mathtt{Th}}(Kv; \mathcal {L}_r)$
,
![]() ${\mathtt{Th}}(vK; \mathcal {L}_{oag})$
. By definition k is perfect and
${\mathtt{Th}}(vK; \mathcal {L}_{oag})$
. By definition k is perfect and
![]() $\Gamma $
is p-divisible, and thus
$\Gamma $
is p-divisible, and thus
![]() $k(\Gamma )$
and
$k(\Gamma )$
and
![]() $k((\Gamma ))$
are perfect. By Lemma 4.1
we may choose
$k((\Gamma ))$
are perfect. By Lemma 4.1
we may choose
![]() $t_1, \dots , t_e \in k((\Gamma ))$
transcendental and algebraically independent over
$t_1, \dots , t_e \in k((\Gamma ))$
transcendental and algebraically independent over
![]() $k(\Gamma )$
and consider the field
$k(\Gamma )$
and consider the field
![]() $k(\Gamma )(t_1, \dots , t_{e-1})$
—by [Reference Fried and Jarden16, Lemma 2.7.2] its imperfection degree is exactly
$k(\Gamma )(t_1, \dots , t_{e-1})$
—by [Reference Fried and Jarden16, Lemma 2.7.2] its imperfection degree is exactly
![]() $e-1$
. Finally, set
$e-1$
. Finally, set
![]() $F = k((\Gamma )) \cap (k(\Gamma )(t_1, \dots , t_{e-1}))^s$
. With
$F = k((\Gamma )) \cap (k(\Gamma )(t_1, \dots , t_{e-1}))^s$
. With
![]() $(R, v_R) = (k(\Gamma ), v_{\Gamma })$
,
$(R, v_R) = (k(\Gamma ), v_{\Gamma })$
,
![]() $(Z, v_Z) = (k((\Gamma )), v_{\Gamma })$
, Assumption
$(Z, v_Z) = (k((\Gamma )), v_{\Gamma })$
, Assumption
![]() $(\otimes )$
is satisfied by Lemma 4.1
. Note the imperfection degree of F is exactly
$(\otimes )$
is satisfied by Lemma 4.1
. Note the imperfection degree of F is exactly
![]() $e-1$
, and
$e-1$
, and
![]() $(Z, v_Z)$
is perfect separably defectless Kaplansky.
$(Z, v_Z)$
is perfect separably defectless Kaplansky.
As there exists an element
![]() $t \in k((\Gamma ))$
transcendental over F, by Theorem 4.8
there exists a field
$t \in k((\Gamma ))$
transcendental over F, by Theorem 4.8
there exists a field
![]() $F(t) \subseteq K_q \subseteq k((\Gamma ))$
such that if
$F(t) \subseteq K_q \subseteq k((\Gamma ))$
such that if
![]() $w = v_{\Gamma }|_{K_q}$
, then
$w = v_{\Gamma }|_{K_q}$
, then
![]() $K_q w = k$
,
$K_q w = k$
,
![]() $wK_q = \Gamma $
,
$wK_q = \Gamma $
,
![]() $\mathbb {F}_p[z]$
is
$\mathbb {F}_p[z]$
is
![]() $\mathcal {L}_{val}$
-definable in
$\mathcal {L}_{val}$
-definable in
![]() $K_q$
where
$K_q$
where
![]() $z \in k(\Gamma )$
is transcendental over
$z \in k(\Gamma )$
is transcendental over
![]() $\mathbb {F}_p$
, and if
$\mathbb {F}_p$
, and if
![]() $a \in k((\Gamma ))\setminus K_q$
is pliant over
$a \in k((\Gamma ))\setminus K_q$
is pliant over
![]() $K_q$
, then
$K_q$
, then
![]() $q | [K_q(a) : K_q]$
.
$q | [K_q(a) : K_q]$
.
-
If e > 0: “pliant” will refer to separably algebraic elements. By the construction of
 $K_q$
as a union of separable extensions of
$K_q$
as a union of separable extensions of
 $F(t)$
,
$F(t)$
,
 $K_q/k(\Gamma )(t_1, \dots , t_{e-1}, t)$
is separably algebraic and has degree of imperfection e by [Reference Fried and Jarden16, Lemma 2.7.3].
$K_q/k(\Gamma )(t_1, \dots , t_{e-1}, t)$
is separably algebraic and has degree of imperfection e by [Reference Fried and Jarden16, Lemma 2.7.3]. -
If e = 0: “pliant” will refer to algebraic elements. As noted in Remark 4.2 ,
 $K_q$
is perfect.
$K_q$
is perfect.
In either case,
![]() $K_q$
is an equicharacteristic p nontrivially valued field of imperfection degree e, with residue field k and value group
$K_q$
is an equicharacteristic p nontrivially valued field of imperfection degree e, with residue field k and value group
![]() $\Gamma $
. We will verify the henselianity axioms
$\Gamma $
. We will verify the henselianity axioms
![]() $\varphi _1, \dots , \varphi _{q-1}$
are satisfied. Let
$\varphi _1, \dots , \varphi _{q-1}$
are satisfied. Let
![]() $l < q$
and fix
$l < q$
and fix
![]() $a_0, \dots a_{l-2} \in \mathfrak {m}_{w}$
. Suppose
$a_0, \dots a_{l-2} \in \mathfrak {m}_{w}$
. Suppose
![]() $X^l + X^{l-1} + a_{l-2}X^{l-2} + \dots + a_0 = 0$
has no solution in
$X^l + X^{l-1} + a_{l-2}X^{l-2} + \dots + a_0 = 0$
has no solution in
![]() $K_q$
—however there exists a solution
$K_q$
—however there exists a solution
![]() $\alpha \in K_q^h$
, and
$\alpha \in K_q^h$
, and
![]() $K_q^h \subseteq k((\Gamma ))$
by the universal property of henselisations [Reference Engler and Prestel13, Theorem 5.2.2]. Then
$K_q^h \subseteq k((\Gamma ))$
by the universal property of henselisations [Reference Engler and Prestel13, Theorem 5.2.2]. Then
![]() $K_q(\alpha )/K_q$
is a finite proper extension; moreover,
$K_q(\alpha )/K_q$
is a finite proper extension; moreover,
![]() $\alpha $
is pliant over
$\alpha $
is pliant over
![]() $K_q$
as
$K_q$
as
![]() $K_q(\alpha ) \subseteq K_q^h \subseteq K_q^s \subseteq \widetilde {K_q}$
. By Theorem 4.8
,
$K_q(\alpha ) \subseteq K_q^h \subseteq K_q^s \subseteq \widetilde {K_q}$
. By Theorem 4.8
,
![]() $q|[K_q(\alpha ) : K_q]$
; however
$q|[K_q(\alpha ) : K_q]$
; however
![]() $q> l$
and
$q> l$
and
![]() $[K_q(\alpha ) : K_q] \leq l$
; a contradiction.
$[K_q(\alpha ) : K_q] \leq l$
; a contradiction.
Let Q be the set of primes
![]() $q> p$
and
$q> p$
and
![]() $\mathcal {U}$
a nonprincipal ultrafilter on Q. Let
$\mathcal {U}$
a nonprincipal ultrafilter on Q. Let
![]() $\mathbb {K} = \prod _{q \in Q} K_q / \mathcal {U}$
; by Łoś’ Theorem,
$\mathbb {K} = \prod _{q \in Q} K_q / \mathcal {U}$
; by Łoś’ Theorem,
![]() $\mathbb {K}$
is an equicharacteristic p henselian nontrivially valued field, of imperfection degree e, and residue field
$\mathbb {K}$
is an equicharacteristic p henselian nontrivially valued field, of imperfection degree e, and residue field
![]() $\mathcal {L}_r$
-elementarily equivalent to
$\mathcal {L}_r$
-elementarily equivalent to
![]() $Kv$
and value group
$Kv$
and value group
![]() $\mathcal {L}_{oag}$
-elementarily equivalent to
$\mathcal {L}_{oag}$
-elementarily equivalent to
![]() $vK$
. Furthermore,
$vK$
. Furthermore,
![]() $\mathbb {K}$
is separably defectless. Indeed, given
$\mathbb {K}$
is separably defectless. Indeed, given
![]() $M \in \mathbb {N}_{>0}$
,
$M \in \mathbb {N}_{>0}$
, ![]() for all primes
for all primes
![]() $q> M^M$
by Lemma 5.7
. Hence, by Łoś’ Theorem,
$q> M^M$
by Lemma 5.7
. Hence, by Łoś’ Theorem, ![]() for all
for all
![]() $M \geq 1$
. By [Reference Delon10, Théorème 3.1],
$M \geq 1$
. By [Reference Delon10, Théorème 3.1],
![]() $\mathbb {K} \equiv _{\mathcal {L}_{val}}\! K$
.
$\mathbb {K} \equiv _{\mathcal {L}_{val}}\! K$
.
Let T be a finite subtheory of
![]() ${\mathtt{Th}}(K; \mathcal {L}_{val})$
. As
${\mathtt{Th}}(K; \mathcal {L}_{val})$
. As
![]() $\mathbb {K} \models T$
, for some
$\mathbb {K} \models T$
, for some
![]() $q \in Q$
we have
$q \in Q$
we have
![]() $K_q \models T$
. By Theorem 4.8 and Corollary 1.8
,
$K_q \models T$
. By Theorem 4.8 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable; hence T is undecidable as required.
${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable; hence T is undecidable as required.
Finally, if
![]() $\mathcal {O}_v \subseteq K$
is
$\mathcal {O}_v \subseteq K$
is
![]() $\mathcal {L}_r$
-definable by the formula
$\mathcal {L}_r$
-definable by the formula
![]() $\varpi (x, \overline {y})$
(where
$\varpi (x, \overline {y})$
(where
![]() $\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
$\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
![]() $\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
$\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
![]() $S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
$S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
![]() $K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
$K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
![]() ${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
Corollary 5.9.
-
(1) If
 $(K, v)$
is an NIP henselian nontrivially valued field,
$(K, v)$
is an NIP henselian nontrivially valued field,
 ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable. Furthermore if
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable. Furthermore if
 $\mathcal {O}_v$
is
$\mathcal {O}_v$
is
 $\mathcal {L}_r$
-definable in K, then K is finitely undecidable as a field.
$\mathcal {L}_r$
-definable in K, then K is finitely undecidable as a field. -
(2) Every infinite dp-finite field is finitely undecidable.
-
(3) Assuming the NIP Fields Conjecture, every infinite NIP field is finitely undecidable.
Proof
-
(1) If
 $(K, v)$
is equicharacteristic 0 or mixed characteristic, this is a result of Corollary 4.10/Theorem 5.3
. If
$(K, v)$
is equicharacteristic 0 or mixed characteristic, this is a result of Corollary 4.10/Theorem 5.3
. If
 $(K, v)$
is positive equicharacteristic then by Anscombe–Jahnke it is separably defectless Kaplansky (Theorem 5.6
); hence its
$(K, v)$
is positive equicharacteristic then by Anscombe–Jahnke it is separably defectless Kaplansky (Theorem 5.6
); hence its
 $\mathcal {L}_{val}$
-theory is finitely undecidable by Theorem 5.8
.
$\mathcal {L}_{val}$
-theory is finitely undecidable by Theorem 5.8
. -
(2) By the work of JohnsonFootnote 8 [Reference Johnson27, Corollary 4.16], every infinite dp-finite field K is either algebraically closed, real closed, or admits a non-trivial definable henselian valuation. If K is algebraically or real closed, it is finitely undecidable by [Reference Ziegler49, Corollary, p. 270]. Otherwise K has an
 $\mathcal {L}_r$
-definable valuation v. As K is dp-finite,
$\mathcal {L}_r$
-definable valuation v. As K is dp-finite,
 ${\mathtt{Th}}(K; \mathcal {L}_r)$
is NIP (following from [Reference Simon45, Observation 4.13]), and hence
${\mathtt{Th}}(K; \mathcal {L}_r)$
is NIP (following from [Reference Simon45, Observation 4.13]), and hence
 ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is NIP as the valuation is
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is NIP as the valuation is
 $\mathcal {L}_r$
-definable. Thus K is finitely undecidable, from (1).
$\mathcal {L}_r$
-definable. Thus K is finitely undecidable, from (1). -
(3) Recall Theorem 3.11 , where assuming the NIP Fields Conjecture one can conclude every infinite NIP field K is either separably closed (hence finitely undecidable by [Reference Ziegler49, Corollary, p. 270]/Corollaries 3.7 and 3.8 ), real closed (hence finitely undecidable by [Reference Ziegler49, Corollary, p. 270]), or admits a nontrivial
 $\emptyset $
-
$\emptyset $
-
 $\mathcal {L}_r$
-definable henselian valuation. In this case, K is finitely undecidable by (1).
$\mathcal {L}_r$
-definable henselian valuation. In this case, K is finitely undecidable by (1).
Example 5.10. We present some finitely undecidable fields, and some open questions, as a consequence of this work.
-
(1) Let
 $(K, v)$
be any algebraic valued field extension of
$(K, v)$
be any algebraic valued field extension of
 $(\operatorname {\mathbb {Q}}_p, v_p)$
with non-divisible value group. By [Reference Koenigsmann32, Lemma 3.6], the valuation is
$(\operatorname {\mathbb {Q}}_p, v_p)$
with non-divisible value group. By [Reference Koenigsmann32, Lemma 3.6], the valuation is
 $\emptyset $
-
$\emptyset $
-
 $\mathcal {L}_r$
-definable. By Theorem 5.3
, K is a finitely undecidable field.
$\mathcal {L}_r$
-definable. By Theorem 5.3
, K is a finitely undecidable field. -
(2) It is unknown if
 $\mathbb {F}_p((t))$
is finitely undecidable. (Equally one can consider the finite undecidability of
$\mathbb {F}_p((t))$
is finitely undecidable. (Equally one can consider the finite undecidability of
 ${\mathtt{Th}}(\mathbb {F}_p((t)); \mathcal {L}_{val})$
, as the valuation ring
${\mathtt{Th}}(\mathbb {F}_p((t)); \mathcal {L}_{val})$
, as the valuation ring
 $\mathbb {F}_p[[t]]$
is
$\mathbb {F}_p[[t]]$
is
 $\emptyset $
-
$\emptyset $
-
 $\mathcal {L}_r$
-definable in
$\mathcal {L}_r$
-definable in
 $\mathbb {F}_p((t))$
by, e.g., [Reference Koenigsmann32, Lemma 3.6].) More generally if
$\mathbb {F}_p((t))$
by, e.g., [Reference Koenigsmann32, Lemma 3.6].) More generally if
 $F\!/\mathbb {F}_p$
is any algebraic extension, the finite undecidability of
$F\!/\mathbb {F}_p$
is any algebraic extension, the finite undecidability of
 $F((t))$
—or of
$F((t))$
—or of
 ${\mathtt{Th}}(F((t)); \mathcal {L}_{val})$
—is an open question.
${\mathtt{Th}}(F((t)); \mathcal {L}_{val})$
—is an open question.
Recall the notion of t-henselianity: a field is t-henselian if it can be equipped with a topology compatible with the field operations, behaving very much like the topology arising from a nontrivial valuation, satisfying a “topological” Hensel’s Lemma. This notion was introduced by Prestel and Ziegler [Reference Prestel and Ziegler40], and the topology shown to be
![]() $\mathcal {L}_r$
-definable in nonseparably closed fields in [Reference Prestel38, p. 203]. Using saturation we may equally state (as Anscombe and Jahnke [Reference Anscombe and Jahnke1, p. 872] do) that a field is t-henselian if it is
$\mathcal {L}_r$
-definable in nonseparably closed fields in [Reference Prestel38, p. 203]. Using saturation we may equally state (as Anscombe and Jahnke [Reference Anscombe and Jahnke1, p. 872] do) that a field is t-henselian if it is
![]() $\mathcal {L}_r$
-elementarily equivalent to a field L which admits a nontrivial henselian valuation, i.e., has a subset
$\mathcal {L}_r$
-elementarily equivalent to a field L which admits a nontrivial henselian valuation, i.e., has a subset
![]() $\mathcal {O} \subseteq L$
that satisfies the definition of a nontrivial henselian valuation ring. (Cf. the discussion in [Reference Prestel and Ziegler40, Section 7] and [Reference Koenigsmann32, Section 3.4].) In some cases we can use t-henselianity—a purely field-theoretic,
$\mathcal {O} \subseteq L$
that satisfies the definition of a nontrivial henselian valuation ring. (Cf. the discussion in [Reference Prestel and Ziegler40, Section 7] and [Reference Koenigsmann32, Section 3.4].) In some cases we can use t-henselianity—a purely field-theoretic,
![]() $\mathcal {L}_r$
-elementary property—to conclude finite undecidability of a field.
$\mathcal {L}_r$
-elementary property—to conclude finite undecidability of a field.
-
(3) Let K be a characteristic 0 t-henselian field with nonuniversal Footnote 9 absolute Galois group. FromFootnote 10 [Reference Jahnke20, Theorem 3.2.3], K is either real closed, separably (= algebraically) closed, or henselian with respect to a nontrivial
 $\emptyset $
-
$\emptyset $
-
 $\mathcal {L}_r$
-definable valuation. Thus K is finitely undecidable, by [Reference Ziegler49, Corollary, p. 270] or Corollary 4.10
or Theorem 5.3
.
$\mathcal {L}_r$
-definable valuation. Thus K is finitely undecidable, by [Reference Ziegler49, Corollary, p. 270] or Corollary 4.10
or Theorem 5.3
. -
(4) Let K be a positive characteristic NIP t-henselian field. If K is separably closed, it is finitely undecidable by Corollary 3.7/3.8 . Otherwise let L be a field with nontrivial henselian valuation v such that
 $L \equiv K$
; note L is not separably closed and NIP as a field. By [Reference Jahnke and Koenigsmann21, Corollary 3.18], L admits a nontrivial
$L \equiv K$
; note L is not separably closed and NIP as a field. By [Reference Jahnke and Koenigsmann21, Corollary 3.18], L admits a nontrivial
 $\emptyset $
-
$\emptyset $
-
 $\mathcal {L}_r$
-definable henselian valuation. Hence K is finitely undecidable, by Corollary 5.9(1).
$\mathcal {L}_r$
-definable henselian valuation. Hence K is finitely undecidable, by Corollary 5.9(1).
Two concrete examples of fields from (3) and (4) are
![]() $\operatorname {\mathbb {C}}((t))$
and
$\operatorname {\mathbb {C}}((t))$
and
![]() $\widetilde {\mathbb {F}_p}((\tfrac {1}{p^{\infty }}\!\operatorname {\mathbb {Z}}))$
, respectively.
$\widetilde {\mathbb {F}_p}((\tfrac {1}{p^{\infty }}\!\operatorname {\mathbb {Z}}))$
, respectively.
-
(5) Boissonneau [Reference Boissonneau5] has recently extended the Anscombe–Jahnke results towards n-dependent valued fields. The class of n-dependent theories was introduced by Shelah in [Reference Shelah42, Section 5(H)] (see [Reference Chernikov, Palacin and Takeuchi9] for further discussion), and is a proper generalisation of NIP (which corresponds to 1-dependent). n-dependence in groups and fields has been studied extensively by Hempel and Chernikov–Hempel [Reference Chernikov and Hempel8, Reference Hempel19].
If
 $(K, v)$
is a positive characteristic n-dependent nontrivially valued field, it is henselian (by [Reference Chernikov and Hempel8, Theorem 3.1]) and separably defectless Kaplansky (by [Reference Boissonneau5, Lemma 3.10]). Thus
$(K, v)$
is a positive characteristic n-dependent nontrivially valued field, it is henselian (by [Reference Chernikov and Hempel8, Theorem 3.1]) and separably defectless Kaplansky (by [Reference Boissonneau5, Lemma 3.10]). Thus
 ${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable, by Theorem 5.8
. Furthermore, by [Reference Hempel19, Proposition 8.4], K is either separably closed (hence finitely undecidable, by Corollary 3.7/3.8
) or admits an
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable, by Theorem 5.8
. Furthermore, by [Reference Hempel19, Proposition 8.4], K is either separably closed (hence finitely undecidable, by Corollary 3.7/3.8
) or admits an
 $\emptyset $
-
$\emptyset $
-
 $\mathcal {L}_r$
-definable nontrivial henselian valuation (separably defectless Kaplansky, by [Reference Boissonneau5, Lemma 3.10]). We conclude from Theorem 5.8
if K is a positive characteristic n-dependent t-henselian field, it is finitely undecidable.
$\mathcal {L}_r$
-definable nontrivial henselian valuation (separably defectless Kaplansky, by [Reference Boissonneau5, Lemma 3.10]). We conclude from Theorem 5.8
if K is a positive characteristic n-dependent t-henselian field, it is finitely undecidable.
One may ask: is every nontrivially henselian valued field, which is finitely undecidable as an
![]() $\mathcal {L}_{val}$
-structure, finitely undecidable as a field? This cannot be concluded easily from Corollary 4.10/Theorem 5.3/Theorem 5.8
, as there exist henselian valued fields which do not admit any nontrivial
$\mathcal {L}_{val}$
-structure, finitely undecidable as a field? This cannot be concluded easily from Corollary 4.10/Theorem 5.3/Theorem 5.8
, as there exist henselian valued fields which do not admit any nontrivial
![]() $\mathcal {L}_r$
-definable henselian valuation, such as the Jahnke–Koenigsmann example [Reference Jahnke and Koenigsmann22, Example 6.2]. Anscombe and Jahnke discuss “henselianity in the language of rings” further in [Reference Anscombe and Jahnke1].
$\mathcal {L}_r$
-definable henselian valuation, such as the Jahnke–Koenigsmann example [Reference Jahnke and Koenigsmann22, Example 6.2]. Anscombe and Jahnke discuss “henselianity in the language of rings” further in [Reference Anscombe and Jahnke1].
Acknowledgements
The author extends his thanks to Professor Ehud Hrushovski, Professor Jochen Koenigsmann, Professor Arno Fehm, Dr. Sylvy Anscombe, and Dr. Konstantinos Kartas for many helpful conversations. Further thanks is due to S. Anscombe for her excellent recommendations on presentation, organisation, and abstraction.