Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-31T19:47:18.709Z Has data issue: false hasContentIssue false
  • English
  • Français

A finite model-theoretical proof of a property of bounded query classes within PH

Published online by Cambridge University Press:  12 March 2014

Leszek Aleksander Kołodziejczyk
Leszek Aleksander Kołodziejczyk*
Affiliation:
Institute of Philosophy, Warsaw University, Krakowskie Przedmieście 3, 00-047 Warsaw, Poland, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

We use finite model theory (in particular, the method of FM-truth definitions, introduced in [MM01] and developed in [K04], and a normal form result akin to those of [Ste93] and [G97]) to prove:

Let m ≥ 2. Then:

(A) If there exists k such that NP⊆ Σm TIME(nk)∩ Πm TIME(nk), then for every r there exists kr such that :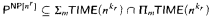

(B) If there exists a superpolynomial time-constructible function f such that NTIME(f)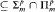, then additionally .

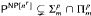This strengthens a result by Mocas [M96] that for any r, .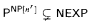

In addition, we use FM-truth definitions to give a simple sufficient condition for the arity hierarchy to be strict over finite models.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 4 , December 2004 , pp. 1105 - 1116
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A83]Ajtai, M., sentences on finite structures, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 1–48.CrossRefGoogle Scholar
[BFFT01]Buhrman, H., Fenner, S., Fortnow, L., and Torenvliet, L., Two oracles that force a big crunch, Computational Complexity, vol. 10 (2001), pp. 93–116.CrossRefGoogle Scholar
[BT94]Buhrman, H. and Torenvliet, L., On the cutting edge of relativization: the resource bounded injury method, ICALP proceedings, Springer-Verlag, Berlin, 1994, pp. 263–273.Google Scholar
[BH91]Buss, S. R. and Hay, L., On truth-lable reducibility to SAT, Information and Computation, vol. 91 (1991), pp. 86–102.CrossRefGoogle Scholar
[F74]Fagin, R., Generalized first-order spectra and polynomial-time recognizable sets, Complexity of Computation, SIAM-AMS Proceedings, vol. 7, American Mathematical Society, Providence, R.I., 1974, pp. 43–73.Google Scholar
[F75]Fagin, R., A spectrum hierarchy, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 21 (1975), pp. 123–134.CrossRefGoogle Scholar
[FLZ92]Fu, B., Li, H., and Zhong, Y., Some properties of exponential time complexity classes, Proceedings of the Structure in Complexity Theory Conference, IEEE Computer Society Press, 1992, pp. 50–57.Google Scholar
[G97]Gottlob, Georg, Relativized logspace and generalized quantifiers over finite ordered structures, this Journal, vol. 62 (1997), no. 2, pp. 545–574.Google Scholar
[HP93]Hájek, P. and Pudlák, P., Metamathematics of first-order arithmetic, Springer-Verlag, Berlin, 1993.CrossRefGoogle Scholar
[K04]Kolodziejczyk, L. A., Truth definitions in finite models, this Journal, vol. 69 (2004), pp. 183–200.Google Scholar
[M96]Mocas, S. E., Separating classes in the exponential-time hierarchy from classes in, PH, Theoretical Computer Science, vol. 158 (1996), pp. 221–231.Google Scholar
[MM01]Mostowski, M., On representing concepts in finite models, Mathematical Logic Quarterly, vol. 47 (2001), pp. 513–523.3.0.CO;2-J>CrossRefGoogle Scholar
[Ste93]Stewart, Iain A., Logical characterizations of bounded query classes, I. Logspace oracle machines, Fundamenta Informaticae, vol. 18 (1993), pp. 65–92.Google Scholar
[Sto77]Stockmeyer, L., The polynomial-time hierarchy, Theoretical Computer Science, vol. 3 (1977), pp. 1–22.Google Scholar
[W90]Wagner, K. W., Bounded query classes, SIAM Journal on Computing, vol. 19 (1990), pp. 833–846.CrossRefGoogle Scholar