Published online by Cambridge University Press: 12 March 2014
Definition 1.1. Suppose that λ ≤ κ are cardinals and Γ is a subset of (κ, κ+). By 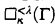 , we mean the principle asserting that there is a sequence 〈Fν | ν ∈ lim(Γ)〉 such that for every ν ∈ lim(Γ), the following hold.
, we mean the principle asserting that there is a sequence 〈Fν | ν ∈ lim(Γ)〉 such that for every ν ∈ lim(Γ), the following hold.
(1) 1 ≤ card(Fν) < λ.
(2) The following hold for every C ∈ Fν.
(a) C ⊆ ν ∩ Γ,
(b) C is club in ν,
(c) o.t.(C) ≤ κ,
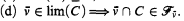
By 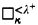 we mean
we mean 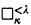 . If Γ = (κ, κ+), then we write
. If Γ = (κ, κ+), then we write 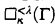 for
for 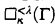 and
and 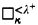 for
for 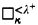 .
.
These weak square principles were introduced in [Sch2, 5.1]. They generalize Jensen's principles □κ and 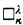 , which are equivalent to
, which are equivalent to 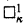 and
and  respectively. Jensen's global □ principle implies □κ for all κ.
respectively. Jensen's global □ principle implies □κ for all κ.
Theorem 1.2. Suppose that 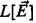 is a core model. Assume that every countable premouse M which elementarily embeds into a level of
is a core model. Assume that every countable premouse M which elementarily embeds into a level of 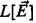 is (ω1 + 1)-iterable. Then, for every κ,
is (ω1 + 1)-iterable. Then, for every κ, 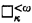 holds in
holds in 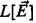 .
.
The minimal non-1-small mouse is essentially a sharp for an inner model with a Woodin cardinal. We originally proved Theorem 1.2 under the assumption that 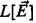 is 1-small, building on [MiSt] and [Sch2]. Some generalizations followed by combining our methods with those of [St2] and [SchSt2]. (For example, the tame countably certified core model Kc satisfies
is 1-small, building on [MiSt] and [Sch2]. Some generalizations followed by combining our methods with those of [St2] and [SchSt2]. (For example, the tame countably certified core model Kc satisfies 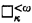 .) In order to eliminate the smallness assumption all together, one replaces our use of the Dodd-Jensen lemma in proofs of condensation properties for
.) In order to eliminate the smallness assumption all together, one replaces our use of the Dodd-Jensen lemma in proofs of condensation properties for 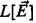 with the weak Dodd-Jensen lemma of [NSt].
with the weak Dodd-Jensen lemma of [NSt].