Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T03:02:34.687Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITARY REDUCIBILITY ON EQUIVALENCE RELATIONS

Published online by Cambridge University Press:  01 December 2016

RUSSELL MILLER  and
KENG MENG NG
RUSSELL MILLER
Affiliation:
DEPARTMENT OF MATHEMATICS QUEENS COLLEGE – C.U.N.Y. 65-30 KISSENA BLVD. FLUSHING, NEW YORK, NY 11367, USA PH.D. PROGRAMS IN MATHEMATICS & COMPUTER SCIENCE C.U.N.Y. GRADUATE CENTER 365 FIFTH AVENUE NEW YORK, NY 10016, USA E-mail: [email protected] Webpage: qcpages.qc.cuny.edu/∼rmiller
KENG MENG NG
Affiliation:
DEPARTMENT OF MATHEMATICS NANYANG TECHNOLOGICAL UNIVERSITY SINGAPORE E-mail: [email protected] Webpage: www.ntu.edu.sg/home/kmng/
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce the notion of finitary computable reducibility on equivalence relations on the domain ω. This is a weakening of the usual notion of computable reducibility, and we show it to be distinct in several ways. In particular, whereas no equivalence relation can be 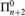${\rm{\Pi }}_{n + 2}^0$ -complete under computable reducibility, we show that, for every n, there does exist a natural equivalence relation which is 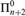${\rm{\Pi }}_{n + 2}^0$ -complete under finitary reducibility. We also show that our hierarchy of finitary reducibilities does not collapse, and illustrate how it sharpens certain known results. Along the way, we present several new results which use computable reducibility to establish the complexity of various naturally defined equivalence relations in the arithmetical hierarchy.

Keywords

computabilitycomputable reducibilityequivalence relationsfinitary reducibilityrecursion theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 4 , December 2016 , pp. 1225 - 1254
Copyright
Copyright © The Association for Symbolic Logic 2016 

References

REFERENCES

Andrews, U., Lempp, S., Miller, J., Ng, K. M., San Mauro, L., and Sorbi, A., Universal computably enumerable equivalence relations , this Journal, vol. 79 (2014), no. 1, pp. 60–88.Google Scholar
Bernardi, C. and Sorbi, A., Classifying positive equivalence relations , this Journal, vol. 48 (1983), no. 3, pp. 529–538.Google Scholar
Calvert, W., Cummins, D., Knight, J. F., and Miller, S., Comparing classes of finite structures . Algebra and Logic, vol. 43 (2004), no. 6, pp. 374–392.CrossRefGoogle Scholar
Calvert, W. and Knight, J. F., Classification from a computable viewpoint . Bulletin of Symbolic Logic, vol. 12 (2006), no. 2, pp. 191–218.Google Scholar
Coskey, S., Hamkins, J. D., and Miller, R., The hierarchy of equivalence relations on the natural numbers under computable reducibility . Computability, vol. 1 (2012), no. 1, pp. 15–38.Google Scholar
[6] Eršov, Yu. L., Teoriya numeratsii , Matematicheskaya Logika i Osnovaniya Matematiki (Russian). [Monographs in Mathematical Logic and Foundations of Mathematics], Nauka, Moscow, 1977.Google Scholar
Fokina, E. B. and Friedman, S.-D., Equivalence relations on classes of computable structures , Computability in Europe: Mathematical Theory and Computational Practice, Springer-Verlag, Berlin, 2009.Google Scholar
Fokina, E. B. and Friedman, S.-D., On ${\rm{\Sigma }}_1^1$ equivalence relations over the natural numbers . Mathematical Logic Quarterly, vol. 58 (2012), 113–124.Google Scholar
Fokina, E. B., Friedman, S.-D., and Törnquist, A., The effective theory of Borel equivalence relations . Annals of Pure and Applied Logic, vol. 161 (2010), no. 7, pp. 837–850.Google Scholar
Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures , this Journal, vol. 54 (1989), no. 3, pp. 894–914.Google Scholar
Gao, S. and Gerdes, P., Computably enumerable equivalence relations . Studia Logica, vol. 67 (2001), no. 1, pp. 27–59.Google Scholar
Goncharov, S. S. and Knight, J. F., Computable structure and non-structure theorems . Algebra and Logic, vol. 41 (2002), no. 6, pp. 351–373.Google Scholar
Ianovski, I., Miller, R., Ng, K. M., and Nies, A., Complexity of equivalence relations and preorders from computability theory , this Journal, vol. 79 (2014), no. 3, pp. 859–881.Google Scholar
Lange, K., Miller, R., and Steiner, R. M., Effective classification of computable structures . Notre Dame Journal of Formal Logic, to appear.Google Scholar
Miller, R., Computable fields and galois theory . Notices of the American Mathematical Society, vol. 55 (2008), no. 7, pp. 798–807.Google Scholar
Miller, R., d-Computable categoricity for algebraic fields , this Journal, vol. 74 (2009), no. 4, pp. 1325–1351.Google Scholar
Rabin, M., Computable algebra, general theory, and theory of computable fields . Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.Google Scholar