Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T01:12:32.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Fibred semantics and the weaving of logics. Part 1: Modal and intuitionistic logics

Published online by Cambridge University Press:  12 March 2014

D. M. Gabbay
D. M. Gabbay*
Affiliation:
Department of Computing, Imperial College of Science, Technology & Medicine, 180 Queen's Gate, London SW1 2BZ, England, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This is Part 1 of a paper on fibred semantics and combination of logics. It aims to present a methodology for combining arbitrary logical systems Li, i ∈ I, to form a new system LI. The methodology ‘fibres’ the semantics 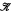i of Li into a semantics for LI, and ‘weaves’ the proof theory (axiomatics) of Li into a proof system of LI. There are various ways of doing this, we distinguish by different names such as ‘fibring’, ‘dovetailing’ etc, yielding different systems, denoted by 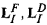etc. Once the logics are ‘weaved’, further ‘interaction’ axioms can be geometrically motivated and added, and then systematically studied. The methodology is general and is applied to modal and intuitionistic logics as well as to general algebraic logics. We obtain general results on bulk, in the sense that we develop standard combining techniques and refinements which can be applied to any family of initial logics to obtain further combined logics.

The main results of this paper is a construction for combining arbitrary, (possibly not normal) modal or intermediate logics, each complete for a class of (not necessarily frame) Kripke models. We show transfer of recursive axiomatisability, decidability and finite model property.

Some results on combining logics (normal modal extensions of K) have recently been introduced by Kracht and Wolter, Goranko and Passy and by Fine and Schurz as well as a multitude of special combined systems existing in the literature of the past 20–30 years. We hope our methodology will help organise the field systematically.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 61 , Issue 4 , December 1996 , pp. 1057 - 1120
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Amati, G. and Pirri, F., Uniform tableaux methods for intuitionistic modal logic I, to appear, in Studio Logica.Google Scholar
[2]Blackburn, P. and de Rijke, M., Why combine logics?, to appear.Google Scholar
[3]Blok, W. J. and Pigozzi, D., Algebraizable logics, Memoirs of AMS (1989), no. 396.Google Scholar
[4]Božić, M. and Došen, K., Models for normal intuitionistic modal logics, Studio Logica, vol. 43 (1984), pp. 217–245.CrossRefGoogle Scholar
[5]Bull, R. A., A modal extension of intuitionist logic, Notre Dame Journal of Formal Logic, vol. 6 (1965).CrossRefGoogle Scholar
[6]Bull, R. A., MIPC as the formalization of an intuitionistic concept of modality, this Journal, vol. 31 (1966), pp. 609–616.Google Scholar
[7]Czelakowski, J., Algebraizability of logic and the deduction theorem, Lecture notes, Colchester, 08 1992, Fourth European Summer school in Logic, Language and Information.Google Scholar
[8]Delgrande, J. P., An approach to default reasoning based on a first order conditional logic, Artificial Intelligence, vol. 36 (1988), pp. 63–90.CrossRefGoogle Scholar
[9]Dörre, J., Gabbay, D., and König, E., Fibred semantics for feature based grammar logic, Journal of Logic, Language and Information, to appear.Google Scholar
[10]Došen, K., Models for stronger normal intuitionistic modal logics, Studia Logica, vol. 44 (1985), pp. 39–70.CrossRefGoogle Scholar
[11]Eiben, A. E., Jánossy, A., and Kurucz, A., Combining logics, Amsterdam, 12 1992.Google Scholar
[12]Ewald, W. B., Intuitionistic tense and modal logic, this Journal, vol. 51 (1986), pp. 166–179.Google Scholar
[13]Fagin, R., Halpern, J. Y., and Vardi, M. Y., A nonstandard approach to the logical omniscience problem, Reasoning about knowledge, TARK 1990 (Parikh, R., editor), Morgan Kaufmann, 1990, pp. 41–55.Google Scholar
[14]Fine, K. and Schurz, G., Transfer theorems for stratified multimodal logics, to appear.Google Scholar
[15]Finger, M. and Gabbay, D., Combining temporal logic systems, Notre Dame Journal of Formal Logic, to appear.Google Scholar
[16]Finger, M. and Gabbay, D. M., Adding a temporal dimension to a logic, Journal of Logic, Language and Information, vol. 1 (1992), pp. 203–233.CrossRefGoogle Scholar
[17]Fischer-Servi, G., On modal logic with an intuitionistic base, StudiaLogica, vol. 36 (1977).Google Scholar
[18]Fischer-Servi, G., Semantics for a class of intuitionistic modal calculi, Italian studies in the philosophy of science (Chiara, M. L. Dalla, editor), D. Reidel, 1980, pp. 59–71.CrossRefGoogle Scholar
[19]Fischer-Servi, G., Axiomatizations for some intuitionistic modal logics, Rend. Sem. Mat. Univ. Politecn. Torino, vol. 42 (1984), pp. 179–194.Google Scholar
[20]Fitch, F. B., Intuitionistic modal logic with quantifiers, Portugalia Mathematica, vol. 7, (1948), pp. 113–118.Google Scholar
[21]Fitting, M., Tableaux for many valued modal logic, Report, 01 25, 1994.Google Scholar
[22]Fitting, M., Logics with several modal operators, Theoria, vol. 35 (1969), pp. 259–266.CrossRefGoogle Scholar
[23]Fitting, M., Many valued modal logics, Fundamenta Informatica, vol. 15 (1991), pp. 235–254.CrossRefGoogle Scholar
[24]Fitting, M., Many valued modal logics II, Fundamenta Informaticae, vol. 17 (1992), pp. 55–73.CrossRefGoogle Scholar
[25]Font, J. M., Modality and possibility in some intuitionistic modal logic, Notre Dame Journal of Formal logic, vol. 27 (1986), pp. 533–546.CrossRefGoogle Scholar
[26]Gabbay, D. M., Fibred semantics and the combination of logics, paper delivered at Logic Colloquium 1992, Veszprém, Hungary, 08 1992,; a version of the notes is published as a Technical Report No 36, by the University of Stuttgart, Sonderforschungbereich 340, Azenbergstr 12, 70174 Stuttgart, Germany, 1993.Google Scholar
[27]Gabbay, D. M., Conditional implication and nonmonotonic consequence, Views on conditionals (del Cerro, L. F.et al., editors), 1995, OUP, pp. 347–369.Google Scholar
[28]Gabbay, D. M., Fibred semantics and the weaving of logic, part 3, How to make your logic fuzzy, Imperial College, 1995, draft.Google Scholar
[29]Gabbay, D. M., Fibred semantics and the weaving of logics, part 2, Logic Colloquium 92 (Czermak, L., Gabbay, D., and de Rijke, M., editors), 1995, SILLI/CUP, pp. 95–113.Google Scholar
[30]Gödel, K., Eine Interpretation des intuitistischen aussagenkalküls, Ergebnisse eines Mathematischen Kolloquiums, vol. 4 (1933), pp. 39–40.Google Scholar
[31]Goranko, V. and Passy, S., Using the universal modality: Gains and questions, Journal of Logic and Computation, vol. 2 (1992), pp. 5–30.CrossRefGoogle Scholar
[32]Jones, A. J. I., Towards a formal theory of defeasible deontic conditionals, Annals of Mathematics and Artificial Intelligence, to appear.Google Scholar
[33]Jones, A. J. I. and Pörn, I., Ideality, subideality and denontic logic, vol. 65, 1985.Google Scholar
[34]Jones, A. J. I. and Pörn, I., ‘Ought’ and ‘must’, Synthese, vol. 66 (1986).CrossRefGoogle Scholar
[35]Kracht, M. and Wolter, F., Properties of independently axiomatizable bimodal logics, this Journal, vol. 56 (1991), pp. 1469–1485.Google Scholar
[36]Lakemeyer, G., Tractable meta-reasoning in propositional logics of belief, IJCAI-87, 1987, pp. 402–408.Google Scholar
[37]Levesque, H., A logic of implicit and explicit belief, AAI-84, 1984, pp. 198–202.Google Scholar
[38]Ono, H., On some intuitionistic modal logic, Publications Research Institute Mathematical Science, vol. 13 (1977), pp. 687–722.CrossRefGoogle Scholar
[39]Ono, H., Some problems in intermediate predicate logics, Reports on Mathematical Logic, vol. 21 (1987), pp. 55–68.Google Scholar
[40]Pfalzgraf, J., A note on simplexes as geometric configurations, Archiv der Mathematik, vol. 49 (1987), pp. 134–140.CrossRefGoogle Scholar
[41]Pfalzgraf, J., Logical fiberings and polycontextural systems, Fundamentals of artificial intelligence research (Jorrand, Ph. and Kelemen, J., editors), Springer-Verlag, 1991, LNCS 535.Google Scholar
[42]Pfalzgraf, J. and Stokkermans, K., On robotics scenarios and modeling with fibered structures, Automated practical reasoning: Algebraic approaches (Pfalzgraf, J. and Wang, D., editors), Springer series texts and Monographs in Symbolic Computation, Springer-Verlag, 1994.Google Scholar
[43]Prior, A. N., Time and modality, Oxford University Press, 1957.Google Scholar
[44]Suzuki, N. Y., An algebraic approach to intuitionistic modal logics in connection with intermediate predicate logics, Studia Logica, vol. 48 (1988), pp. 141–155.CrossRefGoogle Scholar
[45]Suzuki, N. Y., Kripke bundles for intermediate predicate logics and Kripke frames for intuitionistic modal logics, Studia Logica, vol. 49 (1990), pp. 289–306.CrossRefGoogle Scholar
[46]Wijesekera, D., Constructive modal logic 1, Annals of Pure and Applied Logic, vol. 50 (1990), pp. 271–301.CrossRefGoogle Scholar