Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T23:46:55.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of the constructive ordinals1

Published online by Cambridge University Press:  12 March 2014

Wayne Richter
Wayne Richter*
Affiliation:
Rutgers, The State University, New Brunswick, N.J.
Get access Rights & Permissions [Opens in a new window]

Extract

Kleene [5] mentions two ways of extending the constructive ordinals. The first is by relativizing the set O of notations for the constructive ordinals, using fundamental sequences which are partial recursive in O. In this way we obtain the set OO which provides notations for the ordinals less than ω1O. Continuing the process, the sequence O, OO, 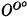, … and the corresponding ordinals 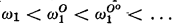are obtained. A second possibility is to define (constructive) higher number classes in which partial recursive functions are used at limit ordinals to provide an “accessibility” mapping from a previously defined number class. The relationship between the ordinals obtained by the two methods of extension has been an open problem. Methods developed in this article are used to show that the two ways of extending the constructive ordinals are equivalent, provided the sets of notations for the higher number classes satisfy certain natural conditions. Equivalence is obtained, not only with respect to ordinals, but also with respect to the forms of the sets of notations for the higher number classes. Specifically, the fundamental fact that the sets of notations for the constructive ordinals are complete Π11 sets generalizes to suitably defined higher number classes. As an application we prove that the ordinals of the Addison and Kleene [1] constructive third number class are exactly the ordinals less than ω1O and the set 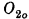of notations for their third number class is recursively isomorphic to OO.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 30 , Issue 2 , June 1965 , pp. 193 - 211
Copyright
Copyright © Association for Symbolic Logic 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Research for this article was begun while the author was a National Science Foundation Predoctoral Fellow. Some of the material presented here is contained in the author's Ph.D. thesis [10] and was presented by title [11] to the American Mathematical Society, February, 1964.

References

REFERENCES

[1]Addison, J. W. and Kleene, S. C., A note on function quantification, Proceedings of the American Mathematical Society, vol. 8 (1957), pp. 1002–1006.CrossRefGoogle Scholar
[2]Dekker, J. C. E., Productive sets, Transactions of the American Mathematical Society, vol. 78 (1955), pp. 129–149.CrossRefGoogle Scholar
[3]Kleene, S. C., On notation for ordinal numbers, this Journal, vol. 3 (1938), pp. 150–155.Google Scholar
[4]Kleene, S. C., Introduction to metamathematics, Amsterdam (North-Holland), Groningen (Noordhoff), New York and Toronto (van Nostrand), 1952.Google Scholar
[5]Kleene, S. C., Hierarchies of number-theoretic predicates, Bulletin of the American Mathematical Society, vol. 61 (1955), pp. 193–213.CrossRefGoogle Scholar
[6]Kleene, S. C., On the forms of the predicates in the theory of constructive ordinals (second paper), American Journal of Mathematics, vol. 77 (1955), pp. 405–428.CrossRefGoogle Scholar
[7]Kreider, D. L. and Rogers, H. Jr., Constructive versions of ordinal number classes, Transactions of the American Mathematical Society, vol. 100 (1961), pp. 325–369.CrossRefGoogle Scholar
[8]Kreisel, G., Shoenfield, J. and Wang, H., Number theoretic concepts and recursive well-orderings, Archiv für Mathematische Logik und Grundlagenforschung, vol. 5 (1960), pp. 42–64.CrossRefGoogle Scholar
[9]Myhill, J., Creative sets, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 97–108.CrossRefGoogle Scholar
[10]Richter, W. H., Systems of notations for the “constructively accessible” ordinals, Ph. D. Thesis Princeton University, 1963.Google Scholar
[11]Richter, W. H., Ordinal systems and generalized 1-function-quantifier-universal sets (Preliminary report), Notices of the American Mathematical Society, Abstract 64T–97, vol. 11 (1964), p. 217.Google Scholar
[12]Smullyan, R. M., Theory of formal systems, Princeton University Press, Princeton, N.J., 1961.CrossRefGoogle Scholar
[13]Spector, C., Recursive well-orderings, this Journal, vol. 20 (1955), pp. 151–163.Google Scholar
[14]Spector, C., Inductively defined sets of natural numbers, Infinitistic methods (Proceedings of the symposium on foundations of mathematics, Warsaw 2–9 09 1959). Oxford, London, New York and Paris, Permagon Press, 1961, pp. 97–102.Google Scholar
[15]Wang, H., Remarks on constructive ordinals and set theory. Summaries of talks presented at the Summer Institute for Symbolic Logic, Cornell University, 1957, 2nd edn., Communications Research Division, Institute for Defense Analyses, Princeton, N.J., 1960, pp. 383–390.Google Scholar